1
i
j
k
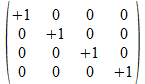

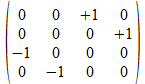
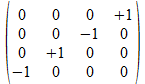
<<>>
<b•a>
<b>
<a>
Rotaties kunnen we modelleren met behulp van het creatief product met een toegevoegde onderscheiding die voor elke stap dezelfde waarde heeft. Dit is mogelijk in het één onderscheiding universum (opgespannen door <<>> en een welgevormde haakuitdrukking x en infimum <ℵ<x>><<ℵ><x>>) met een 2x2 matrix. Hiermee kwantificeren we de mogelijke stappen in de dynamiek van x voor elke situatie waarin de toegevoegde onderscheidingen dezelfde waarde hebben. Maar dit is ook uit te breiden voor x gelijk aan een willekeurige haakuitdrukking.
Alle welgevormde haakuitdrukkingen zijn in het 3&1 patroon uit te drukken, en elk 3&1 patroon kan afgebeeld worden op een atoom in twee onderscheidingen. Om in dat universum rotaties uit te drukken is het voldoende om intensiteiten (positieve getallen) toe te kennen aan de basisvectoren van een welgevormde haakuitdrukking van het twee onderscheidingen universum en dit af te beelden op de 4x4 matrix die de welgevormde haakuitdrukking representeert en die af te beelden is op een quaternion. We gebruiken enkel positieve getallen omdat het plusteken en minteken deel uitmaken van de modellering van de structuur.
We geven hiervan eerst een voorbeeld om de aandacht te richten en vertrekken van een willekeurige welgevormde haakuitdrukking <s•q>⊕r•p⊕r•q⊕s•p. Het is duidelijk dat dit te schrijven is in het formaat r•q•(<r•s>⊕p•q⊕<<>>⊕p•q•r•s) en we hercoderen nu met r•s=a en p•q=b naar het patroon <<>>⊕<a>⊕b⊕a•b, de som van de basisvectoren van de welgevormde haakuitdrukking a<b>. Dus de willekeurige welgevormde haakuitdrukking hebben we voorgesteld als een intensiteit, namelijk r•q, van een eenheid, namelijk a<b>, onder voorwaarde dat het vectorproduct tussen beide niet verschillend is van een nevenschikking (disjunctie).
We gaan a<b> nu als matrix uitdrukken en kiezen voor de reverse Hamilton vertaling. De vertaling van de onderscheidingen in een twee onderscheidingen universum is dan als volgt:
1 |
i |
j |
k |
|
|
|
|
<<>> |
<b•a> |
<b> |
<a> |
De welgevormde haakuitdrukking a<b> is dan:
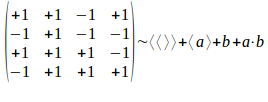
Dus ook:
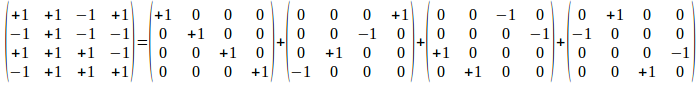
We geven nu elk van die basisvectoren (en dus de matrices in het rechter lid) een positieve intensiteit, namelijk
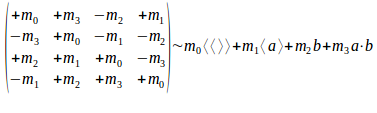
We gebruiken uiteraard de nevenschikking als operatie die de intensiteit met zijn eenheid verbindt omdat we elke eenheid moeten kunnen voorstellen als een creatief product “dat kan geroteerd worden”.
We passen toe dat de determinant van
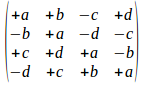 gelijk is aan a4+2a2b2+2a2c2+2a2d2+b4+2b2c2+2b2d2+c4+2c2d2+d4
gelijk is aan a4+2a2b2+2a2c2+2a2d2+b4+2b2c2+2b2d2+c4+2c2d2+d4
Dus, met a=b=c=d=1 is de determinant gelijk aan 16, in modulo 3 is dat dus 1.
Nu interpreteren we de coëfficiënten mi van de termen van de welgevormde haakuitdrukking als haakvector als volgt: m0=cos(φ/2), m1=sin(φ/2)(n-1n1), m2=sin(φ/2)(n-1n2), m3=sin(φ/2)(n-1n3). Hierin nemen we φ=n=(n12+n22+n32)1/2. Zodanig dat de intensiteit van de welgevormde haakuitdrukking wordt: cos(n/2)•<<>>⊕sin(n/2)•n-1•(n1•<a>⊕n2•b⊕n3•a•b). Hierbij is het vectorproduct niet verschillend van de disjunctie behalve voor a•b. De kwantificering herleidt zich dus tot één parameter n, waarvan het kwadraat een som is van drie kwadraten.
We zien onmiddellijk dat we nu door sommige waarden van n ook niet welgevormde haakuitdrukkingen zullen genereren want cos(n/2) kan zowel positief als negatief zijn en ook gelijk zijn aan nul.
Als we nu de eenheden van de quaternionen gebruiken (we geven ze hier weer in vette druk) dan moeten we dit schrijven als cos(n/2)•1+sin(n/2)•n-1•(n1•k+n2•(-j)+n3•(-i)). Als we de onderscheidingen een andere naam geven die doet denken aan de eenheden van quaternionen (we kunnen gelijk wat gebruiken als symbool), dan wordt dit cos(n/2)•<<>>⊕sin(n/2)•n-1•(n1•k⊕n2•<j>⊕n3•<i>). Merk op dat we inbeddingen moeten gebruiken, het teken van de getallen is altijd positief.
De matrix met enkel de intensiteiten is dus
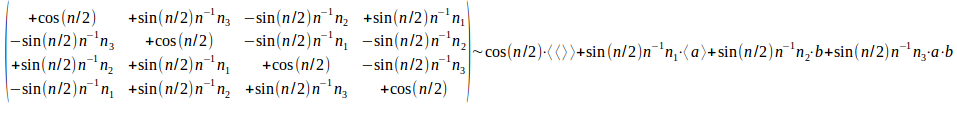
De determinant van deze 4x4 matrix is gelijk aan 1, wat we hieronder bewijzen:
We passen toe dat de determinant van
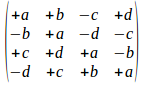 gelijk is aan a4+2a2b2+2a2c2+2a2d2+b4+2b2c2+2b2d2+c4+2c2d2+d4
gelijk is aan a4+2a2b2+2a2c2+2a2d2+b4+2b2c2+2b2d2+c4+2c2d2+d4
Dus, met a=cos(n/2), b=sin(n/2)n3/n, c=sin(n/2)n2/n, d=sin(n/2)n1/n
(cos(n/2))4+2(cos(n/2))2(sin(n/2)n3/n)2+2(cos(n/2))2(sin(n/2)n2/n)2+2(cos(n/2))2(sin(n/2)n1/n)2+(sin(n/2)n3/n)4+2(sin(n/2)n3/n)2(sin(n/2)n2/n)2+2(sin(n/2)n3/n)2(sin(n/2)n1/n)2+(sin(n/2)n2/n)4+2(sin(n/2)n2/n)2(sin(n/2)n1/n)2+(sin(n/2)n1/n)4=
(cos(n/2))4+2(cos(n/2))2(sin(n/2)2{(n3/n)2+(n2/n)2+(n1/n)2}+(sin(n/2))4{(n3/n)4+(n2/n)4+(n1/n)4}+2(sin(n/2)n3/n)2(sin(n/2)n2/n)2+2(sin(n/2)n3/n)2(sin(n/2)n1/n)2+2(sin(n/2)n2/n)2(sin(n/2)n1/n)2=
(cos(n/2))4+2(cos(n/2))2(sin(n/2)2+(sin(n/2))4{(n3/n)4+(n2/n)4+(n1/n)4}+2(sin(n/2)n3/n)2(sin(n/2)n2/n)2+2(sin(n/2)n3/n)2(sin(n/2)n1/n)2+2(sin(n/2)n2/n)2(sin(n/2)n1/n)2=
(cos(n/2))4+2(cos(n/2))2(sin(n/2)2+(sin(n/2))4{(n3/n)4+(n2/n)4+(n1/n)4+2(n3/n)2(n2/n)2+2(n3/n)2(n1/n)2+2(n2/n)2(n1/n)2}=
(cos(n/2))4+2(cos(n/2))2(sin(n/2)2+(sin(n/2))4{(n3/n)2+(n2/n)2+(n1/n)2}2=
(cos(n/2))4+2(cos(n/2))2(sin(n/2)2+(sin(n/2))4=
{(cos(n/2))2+(sin(n/2))2}2=1
QED
We merken ook op dat a2+b2+c2+d2=1 want (cos(n/2))2+(sin(n/2)n3/n)2+(sin(n/2)n2/n)2+(sin(n/2)n1/n)2=(cos(n/2))2+(sin(n/2))2(n12+n22+n32)(n12+n22+n32)-1=(cos(n/2))2+(sin(n/2))2=1.
Hieruit volgt onmiddellijk dat (a, b, c, d) en (-a, -b, -c, -d) dezelfde rotatie kwantificeren. Dus een gekwantificeerde haakuitdrukking en zijn inbedding modelleren dezelfde rotatie.
De interpretatie in het haakformalisme van a2+b2+c2+d2 is ook helder: het is de interne discriminatie van de enige waarde (namelijk <<>> of <>) met zichzelf en kwantificeert dus het onderscheidingen universum.
We hebben hiermee dus ook een eenheidsquaternion geconstrueerd.
De hoek van de rotatie zal bepalen welk soort atoom gemodelleerd wordt: voor een positieve waarde van cos(n/2) wordt een OR-atoom gemodelleerd, voor een negatieve waarde van cos(n/2) wordt een AND-atoom gemodelleerd. Aangezien een gekwantificeerde haakuitdrukking en zijn inbedding dezelfde rotatie modelleren, en elk OR-atoom de inbedding is van een AND-atoom, modelleren we bij een rotatie slechts de helft van de tralie.
Voor een bepaalde waarde van n=(n12+n22+n32)1/2 geven de vier mogelijke combinaties van negatieve of positieve ni welk atoom gemodelleerd wordt. Het feit dat we een hoek kunnen tellen betekent dus dat we geen onderscheid meer kunnen maken tussen de atomen onder invloed van de laatst toegevoegde onderscheiding. Er is bijvoorbeeld geen verschil tussen (-n1)2 en (+n1)2 en dat geldt voor alle combinaties. En inderdaad: als alle onderscheidingen in een tralie dezelfde waarde hebben, noem ze u, wordt de tralie gereduceerd tot de tralie van één onderscheiding in u. Dat betekent dat er maar één onderscheiding meer overschiet en de twee potentiële atomen u en <u> gevormd worden voor n=π (want dan is cos(π/2)=0). In het algemeen is de cosinus niet gelijk is aan nul en dan worden vier eenheden mogelijk: <<>>⊕u, <<>>⊕<u> en hun inbeddingen <>⊕<u> en <>⊕u.
Het is de soort (en dus cos(n/2)) die bepaalt welke combinatie van plus of min een potentiële haakuitdrukking (een 3&1 patroon) of een gecollapste haakuitdrukking (verschillend van een 3&1 patroon) zal modelleren. We demonstreren dat door het voorbeeld met eenvoudige getallen te kwantificeren. We kiezen n1=1, n2=2, n3=3, dus n/2=(1/2).(n12+n22+n32)1/2=(1/2).(14)1/2=1,87082869339
cos1,87082869339=-0,295551127493 en n-1.sin1,87082869339=0,267261241912
cos(n/2)<<>>⊕sin(n/2)n-1(n1<a>⊕n2b⊕n3a•b)=0,295551127493<>⊕0,267261241912(<a>⊕2b⊕3a•b) en dat geeft het patroon voor vier welgevormde haakuitdrukkingen:
0,295551127493<>⊕0,267261241912(<a>⊕2<b>⊕3a•b)
0,295551127493<>⊕0,267261241912(<a>⊕2b⊕3<a•b>)
0,295551127493<>⊕0,267261241912(a⊕2<b>⊕3<a•b>)
0,295551127493<>⊕0,267261241912(a⊕2b⊕3a•b)
en vier gecollapste haakuitdrukkingen:
0,295551127493<>⊕0,267261241912(<a>⊕2<b>⊕3<a•b>)
0,295551127493<>⊕0,267261241912(<a>⊕2b⊕3a•b)
0,295551127493<>⊕0,267261241912(a⊕2<b>⊕3a•b)
0,295551127493<>⊕0,267261241912(a⊕2b⊕3<a•b>)
met de duale haakuitdrukkingen voor de hoek π-n/2 (noteer dat we de getallen als positief blijven beschouwen en het teken door de vectoren gecodeerd wordt), eerst de gecollapste:
0,295551127493<<>>⊕0,267261241912(<a>⊕2<b>⊕3a•b)
0,295551127493<<>>⊕0,267261241912(<a>⊕2b⊕3<a•b>)
0,295551127493<<>>⊕0,267261241912(a⊕2<b>⊕3<a•b>)
0,295551127493<<>>⊕0,267261241912(a⊕2b⊕3a•b)
en de vier welgevormde haakuitdrukkingen:
0,295551127493<<>>⊕0,267261241912(<a>⊕2<b>⊕3<a•b>)
0,295551127493<<>>⊕0,267261241912(<a>⊕2b⊕3a•b)
0,295551127493<<>>⊕0,267261241912(a⊕2<b>⊕3a•b)
0,295551127493<<>>⊕0,267261241912(a⊕2b⊕3<a•b>)
Noteer dus dat er periodiciteit is, niet over een hoek van 2π maar van 4π. Dit is het gevolg van de n/2 in de relatie cos(n/2)<<>>⊕sin(n/2)n-1(n1<a>⊕n2b⊕n3a•b): er ontstaat een afwisseling van welgevormde en gecollapste haakuitdrukkingen die slechts na twee rotaties het oorspronkelijke patroon vertonen.
Dit is een eigenschap van elk element dat in drie dimensies onlosmakelijk met zijn omgeving (iets anders dus) verbonden is (zoals men kan demonstreren door de handpalm 360° te draaien en door slechts na 720° in dezelfde zin doordraaiend, in dezelfde positie terug te kunnen keren, dit wordt ook de Balinese kaarsdans genoemd).
Welgevormde en gecollapste haakuitdrukkingen komen overeen met quaternionen en hun geconjugeerde wanneer we a, b en a•b interpreteren als de drie vectoren k, j, i.
Zoals bekend bij quaternionen, kan ook elke gekwantificeerde haakuitdrukking h gebruikt worden om een andere haakuitdrukking g op een unieke manier te roteren door de constructie hgh-1 waarbij de nevenschikking hier het quaternion product is, het matrix product, een associatief creatief product, of de disjunctie die niet verschillend is van het vectorproduct. De rotatie gebeurt rond de as (n1, n2, n3) in tegenwijzerzin (kijkend van de pijl van de vector naar zijn staart op het nulpunt) en de rotatiehoek is (n12+n22+n32)1/2. De orthogonale eenheidsvectoren zijn dan i, j en k.
Zoals voor quaternionen kunnen we dan ook a, b en a•b afbeelden op drie orthogonale assen in de driedimensionale ruimte. Die quaternionen worden “zuivere” quaternionen genoemd. In het isomorfisme zijn dat dus punten op centraal niveau. Een rotatie behoudt het niveau in de tralie van de vector die geroteerd wordt wat kan gedemonstreerd worden door alle mogelijke combinaties van roterende haakuitdrukkingen g met mogelijke operatoren h te onderzoeken. Een gekwantificeerde haakuitdrukking h die de rotatie bewerkstelligt op g kan uiteraard ook als een zuiver quaternion beschouwd worden en dan is de hoek waaronder geroteerd wordt π (want dan is cos(π/2)=0).
We merken ook op dat h en <h> dezelfde rotatie bewerkstelligen. Inderdaad, (-n1, -n2, -n3) en een rotatie onder een hoek van (2π-n) genereert dezelfde rotatie.
De rotatie met een samenstelling van operatoren wordt gemodelleerd als (h1h2)g(h1h2)-1 en aangezien het matrixproduct een creatief product is met een laatst toegevoegde onderscheiding ℵ (zowel nevenschikking als vectorproduct) geldt: (a⊗b)ℵ-1=(b-1⊗a-1)ℵ en dus (h1h2)g(h2)-1(h1)-1. Dit is eveneens een eigenschap van quaternionen.
We benadrukken dat in het haakformalisme slechts 2 van de drie vectoren nodig zijn om een welgevormde haakuitdrukking te modelleren. De OR atomen in twee onderscheidingen k en j zijn als volgt, en enkel als we de welgevormde haakuitdrukking als haakvector willen voorstellen, is i nodig (de haakuitdrukking heeft altijd minder symbolen nodig dan de haakvector en dit is allesbehalve triviaal):
Haakuitdrukking |
<k><j> |
k<j> |
<k>j |
kj |
Haakvector |
<<>>⊕k⊕j⊕<i> |
<<>>⊕<k>⊕j⊕i |
<<>>⊕k⊕<j>⊕i |
<<>>⊕<k>⊕<j>⊕<i> |
Bitstring in k en j |
---+ |
--+- |
-+-- |
+--- |
Matrix |
|
|
|
|
We zijn vertrokken van een willekeurige welgevormde haakuitdrukking. Telkens kan deze uitdrukking geschreven worden in de eenvoudiger vorm <s•q>⊕r•p⊕r•q⊕s•p waarbij p, q, r en s welgevormde uitdrukkingen kunnen zijn in gelijk welke grootte van universum, universa die eventueel enkel in dit patroon met elkaar kunnen interageren. Elke 2-vector uit deze vorm kan gebruikt worden als toegevoegde onderscheiding in een creatief product waarbij deze onderscheiding ingebouwd wordt in de tralie. Deze uitdrukking kan ook op vier manieren geschreven worden als een vectorproduct van een van de 2-vectoren uit de som en een AND-atoom of OR-atoom in twee onderscheidingen in r•s en p•q. Telkens kunnen we die twee eenheden (r•s en p•q) en hun twee afgeleide eenheden (naar de toegevoegde onderscheiding) <<>> en p•q•r•s terug weer uitbreiden naar een vorm met intensiteiten die met elkaar gerelateerd zijn. Die intensiteiten moeten niet ingebouwd worden in de tralie en zijn dus geen eenheden, ze zijn onafhankelijk van de eenheden van de tralie. Meer dan twee eenheden en hun twee afgeleiden hebben we niet nodig. We worden hierin niet beperkt in onze keuze, tenzij door de relaties die we hier naar voor gebracht hebben.
De eenheden van het haakformalisme kunnen dus vanuit modulo2, modulo3 en modulo4 opgebouwd worden, waarmee dan onmiddellijk een moduloN beschikbaar wordt als benadering van een modulo2π.
Dit is een opmerkelijke conclusie omdat we hiermee bewijzen dat meer dan vier eenheden niet nodig zijn om gelijk welke potentiële en complexe werkelijkheid te beschrijven in ervaarbare gebeurtenissen. Die eenheden zijn niet a priori bepaald, maar eens we de (logische, causale) patronen herkennen die in het haakformalisme beschreven worden, kunnen we vier eenheden en hun intensiteiten veronderstellen en waarneembaar maken.