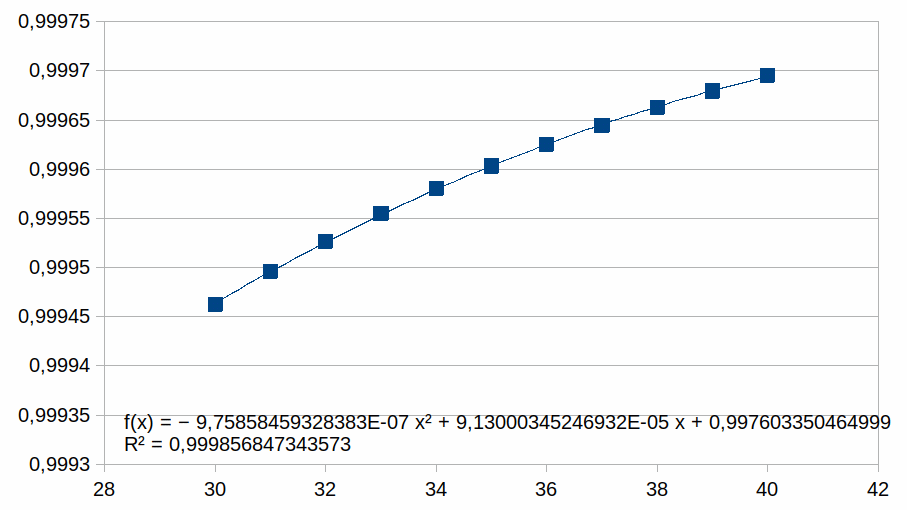We hebben aangetoond dat een
Lorentz boost de relatie van evenwicht uitdrukt tussen
verhoudingen
en dus ook processnelheden.
We hebben die relatie van evenwicht als een som uitgedrukt
(v01+v12+v20=0) maar ook als een
product ((v01)(v12)(v20)=0).
Dat maakt duidelijk dat we een nieuwe eenheid moeten veronderstellen
(namelijk: de standaard eenheid is nul voor een som en 1 voor een
product). Deze eenheid hebben we gecreëerd door de verhoudingen
expliciet voor te stellen met teller en noemer. De eenheid is het
inverse product 1/(n0+n1)(n1+n2)(n2+n0)
en de beide leden van de vergelijking v01+v12+v20=(v01)(v12)(v20)
geven dezelfde intensiteit van die ene eenheid. Die eenheid is van
het type 1/(1+k) met k de
eigenwaarde van een feedback proces (1+k is mogelijks een
veelterm zoals duidelijk wordt in de voorstelling
(n0)(n1)(n2)/(1+n1/n0)(1+n2/n1)(1+n0/n2)).
Een eigenwaarde gelijk aan nul
staat dan voor geen feedback. Een product
van eigenwaarden modelleert simultaneïteit. Het product
(n0)(n1)(n2)/(1+n1/n0)(1+n2/n1)(1+n0/n2))
onderbouwt de driedimensionale ruimte. De relatie met feedback maakt
nog maar eens duidelijk dat we processen beschouwen die een spoor ni
achterlaten. We beschouwen de getallen niet als coördinaten in
referentieframes, en dit maakt nog maar eens een belangrijk verschil
met de klassieke interpretatie duidelijk. Zo we willen kunnen we
gelijk welke interpretatie van tijd gebruiken zolang de interpretatie
gebaseerd is op een processtap tussen twee elkaar uitsluitende
toestanden, processtap die ons in staat stelt een verschil waar te
nemen, een “verschil per stap”, een “verschil per
vrijheidsgraad T”. In sommige universa is een verschil per stap
kleiner of groter dan in andere (wat men tijdrek noemt, en dat vanuit
gelijk welk standpunt) en in sommige universa zijn bepaalde
verschillen per stap niet waarneembaar omdat de onderscheidingen
hiervoor niet beschikbaar zijn, de waarnemingsresolutie is te klein.
Elk universum, hoe groot het ook zou zijn (gemeten aan het aantal de
toestanden 2n), kan met behulp van minder onderscheidingen
gemodelleerd worden. We moeten wel een grootste onderscheidingen
universum veronderstellen want meer onderscheidingen zijn nog niet
gecreëerd (of beschikbaar) en het grootste universum is enkel te
beschrijven met de onderscheiding met laagste frequentie (we hebben
daarvoor “lang genoeg gewacht”).
We hebben bewezen dat we een verhouding kunnen beschouwen als een
getal dat we interpreteren als de intensiteit van een toestand,
een atoom in een tralie, of in het binair model van het
haakformalisme als een getal dat de intensiteit geeft van één bit.
De intensiteit van de eenheid van één bit kan altijd als een
kwadraat voorgesteld worden (dit als gevolg van de interne
discriminatie),
dus de universele eenheid is een kwadraat en kunnen we voorstellen
als (1±z)-2 want het
meest universele patroon waarmee getallen kunnen opgebouwd worden die
zich als eenheid met intensiteit kunnen gedragen is
(1±z)-m=((1±z)-2)m/2.
We gebruiken hier het symbool z (“frequentieverschuiving”,
meer gekend als “roodverschuiving”) zoals dit gekend is bij
golfverschijnselen omdat we op die manier de relatie met trillingen,
golfverschijnselen
en klokken willen onderzoeken (de entiteit, het meetinstrument dat
sporen achterlaat die alleen maar kunnen toenemen) op het meest
abstracte niveau (frequenties van (on)zekerheid). We kunnen (1+z)
interpreteren als de dimensieloze parameter (schaalfactor) die we
kunnen berekenen vanuit het verschil van een golflengte G of
golffrequentie F van elektromagnetische straling, parameters die
gerelateerd zijn door de verschaling GF=c met c de lichtsnelheid. GF
is hierdoor een processnelheid die een eenheidsfunctie vervult en ook
een energiedensiteit
(de verhouding “intensiteit per bit”) in de meer abstracte
interpretatie.
z=±(Gwaargenomen-Guitgezonden)/Guitgezonden
Dit is een verschil van verhoudingen, dus
1±z=±Gwaargenomen/Guitgezonden is een
verhouding die de schaal tussen twee golflengtes kwantificeert.
of ook
z=±(Fuitgezonden-Fwaargenomen)/Fwaargenomen
Dit is een verschil van verhoudingen, dus
1±z=±Fuitgezonden/Fwaargenomen is een
verhouding die de schaal tussen twee frequenties kwantificeert.
Dit zijn relaties van een meting (“waargenomen hier en
nu”) tot een hypothese (“uitgezonden daar en dan”).
Een verschil hebben we als een golflengte
gemodelleerd en we hebben benadrukt dat dit een heel abstract begrip
is. Een golflengte is slechts waarneembaar na een (a priori ongekend)
aantal stappen. “Pas na een onbekend aantal stappen wordt
“hetzelfde” waargenomen” is de beschrijving van een “cyclisch
verschijnen van iets”, een golfverschijnsel. De halve golflengte is
dan het interval tussen twee waarnemingen met zekerheid. We kunnen
veronderstellen dat er “onderliggend” meer stappen zouden kunnen
onderscheiden worden maar dat is een hypothese, onwaarneembaar met
het proces voor handen, enkel als hypothese te formuleren en als
hypothetische getallen voor te stellen. We zien ook in dat niet
alleen “snelheid” maar ook “frequentie” een begrip is dat een
aantal processtappen kan kwantificeren. Inderdaad is een frequentie
een manier om een “hoeveelheid per seconde” aan te geven (en niet
het meer specifieke (gedimensioneerde) “afstand per seconde”) en
we kunnen dat interpreteren als “de veelvuldigheid in een stap”,
een “densiteit” omdat we wel een proces moeten kiezen met elkaar
uitsluitende stappen om “seconde” te kunnen meten. De seconde is
procesafhankelijk. We hebben dat
inzicht op een nieuwe manier gemodelleerd en dan de frequentie
geïnterpreteerd als “de veelvuldigheid van zekerheid”, het
aantal stappen dat onderscheiden kan worden, a priori onbekend. We
hebben beklemtoond dat dit aantal enkel te benaderen is, wat
duidelijk wordt door de keuze van een bepaalde resolutie voor π. Dat
allemaal hebben we afgeleid zonder ergens meer fysische
veronderstellingen te moeten aannemen dan de veronderstelling van
“waarneming van iets en daaropvolgende waarneming van hetzelfde”.
Dit is dus niet een uitsluitend ruimtelijk fenomeen. Een klassieke
golfvergelijking
Acos(2πtf-2πx/λ+φ) met A de amplitude, λ de golflengte, f de
frequentie en φ de fase, is niet meer of minder dan de uitdrukking
van een repetitief patroon van getallen tussen twee extremen “in de
loop van” een proces (dus met een monotoon toenemende of monotoon
afnemende parameter) waarvan de getallen zich met zekerheid herhalen.
We kunnen ook interpreteren dat de reeks x en de reeks t in dezelfde
eenheid kunnen uitgedrukt worden, juist dank zij f en λ. Als het
onbekend aantal stappen verschaald wordt, zullen we dat zien aan de
golflengte of de frequentie. Dat gaan we nu modelleren.
De eenheid van het type 1/(1+k) is te
schrijven als (1-n)/(1+n) voor een k=2n/(1-n). Dat is een lineaire
transformatie. Het patroon (ni-ni+1)/(ni+ni+1)
of (1-k)/(1+k)
is niet anders dan het verschil van twee kwadraten (1-m2)
en genereert een (lineaire) Lorentz
transformatie. Maar we hebben ook een nieuwe transformatie van de
verhouding (1-n)/(1+n) onderzocht: we
bewezen
onder welke voorwaarde een verschil van kwadraten gelijk is aan een
kwadraat (dat kennen we als de stelling van Pythagoras). Dit
maakt ook een geometrische interpretatie mogelijk als toepassing,
maar ook nu zullen we geen geometrische intuïties nodig hebben in
het onderzoek naar de gevolgen van deze veronderstelling (geometrie
leiden we af in het haakformalisme uit een
som gelijk aan nul). We kunnen dan veronderstellen dat de relatie
(1-k)/(1+k) zou kunnen behouden worden en dat is de uitdrukking van
“patroon” en “relativiteit”. Stel (1-k)/(1+k)=v, dan geldt
(1-v)/(1+v)=k.
Laten we daarom de Pythagorese relatie veronderstellen:
(1+z)-2=(1-m2)=(1-k)/(1+k). Hieruit volgt dat
(1+z)2=(1+k)/(1-k). Hieruit volgt:
(1+z)2(1-k)=(1+k)
(1+z)2-k(1+z)2=(1+k)
(1+z)2-1=k(1+z)2+k
2z+z2=k(2+2z+z2)
k=(2z+z2)/(2+2z+z2)
Hieruit volgt:
1+k=1+(2z+z2)/(2+2z+z2)=(2+2z+z2+2z+z2)/(2+2z+z2)=2(1+2z+z2)/(2+2z+z2)=2(1+z)2/(1+(1+z)2)
Dat betekent zowel
k=(2(1+z)2/(1+(1+z)2))-1
als
2/(1+k)=1+(1+z)-2
Voor z=0 is k=0.
Uit de gedetailleerde afleiding volgt dat deze uitdrukking geldt
voor zowel z>0 als voor z<0, (1+z) of (1-z) geven immers
hetzelfde patroon.
De eigenwaarde k als functie van (1±z)
We kunnen de schaal
van de nieuwe eenheid z relateren tot de verschaling van k door de
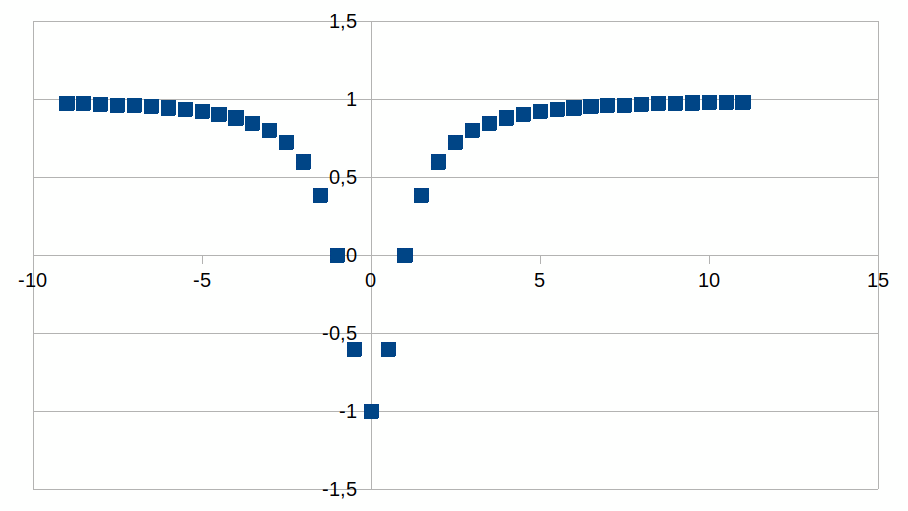
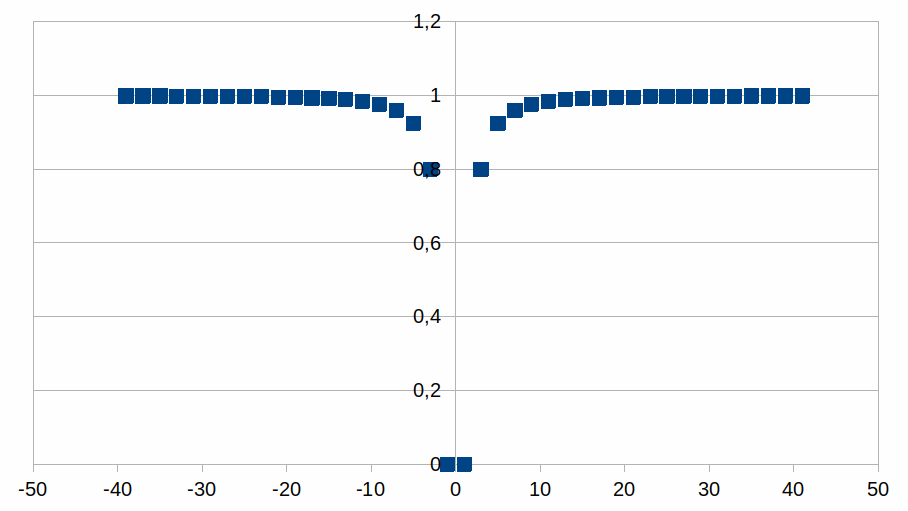
grafiek te bestuderen van k=(2(1±z)2/(1+(1±z)2))-1
als functie van (1±z).
We doen dat voor de intensiteit van S×z waarbij S de verschaling van
de eenheid z voorstelt en dus de verschaling van het aantal stappen.
De eenheid z, dus z=1 moeten we als volgt interpreteren:
z=(Fuitgezonden-Fwaargenomen)/Fwaargenomen
dus z=1 is Fwaargenomen=(Fuitgezonden-Fwaargenomen)
dus 2Fwaargenomen=Fuitgezonden of dus
2Fwaargenomen/Fuitgezonden=1=z
We laten z zowel negatief als positief zijn. In de eerste kolom
kiezen we het getal S en verschalen we dus de abscis, in de tweede
kolom stellen we k voor en de derde kolom geeft een benadering van
die grafiek als polynoom van orde 8 voor positieve k. We voegen een
bespreking toe in de laatste kolom.
S
|
Grafiek
van k in functie van (1+z) voor 40 stappen
|
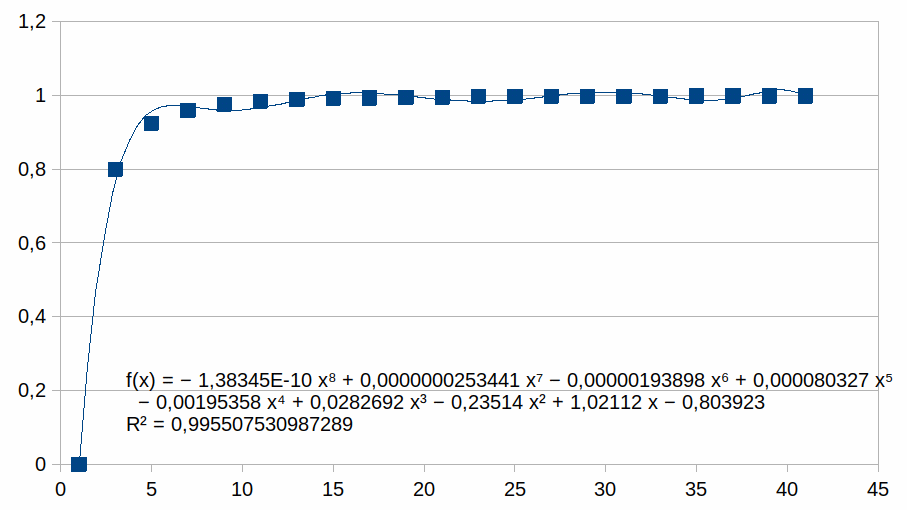
Polynoom
van orde 8 voor positieve k vanaf 0
|
Bespreking:
het aantal stappen die een positieve k genereren zijn niet beperkt
maar bereiken nooit een k=1.
|
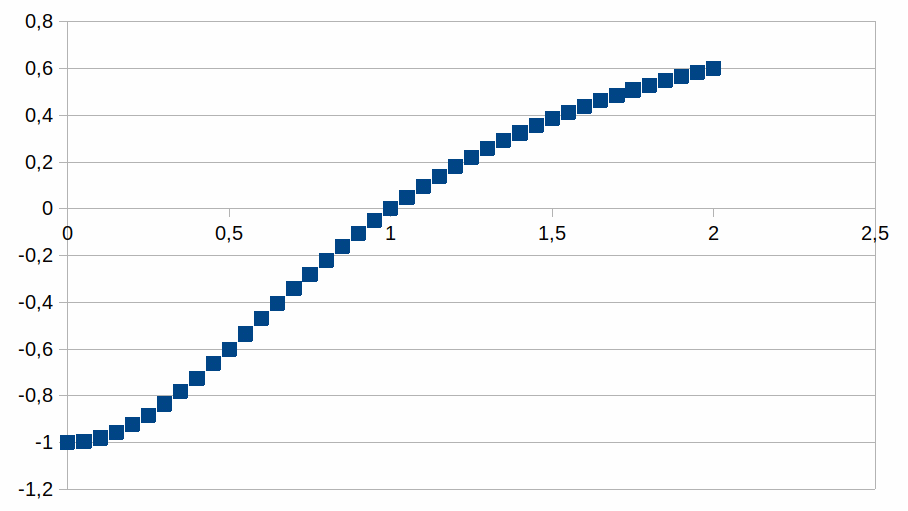
0,05
|
|

|
Een
k=-1 kan bereikt worden voor een z=-1, maar kan niet nog meer
negatief worden.
|
0,1
|
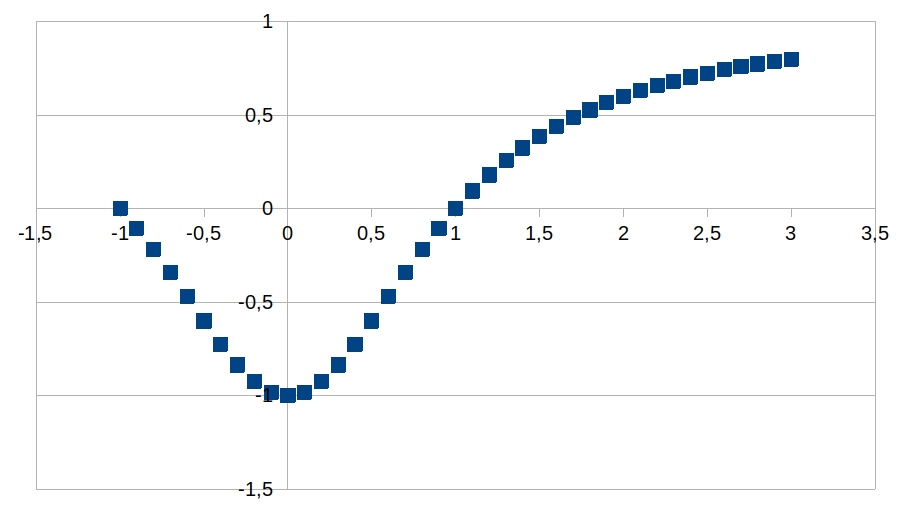
|
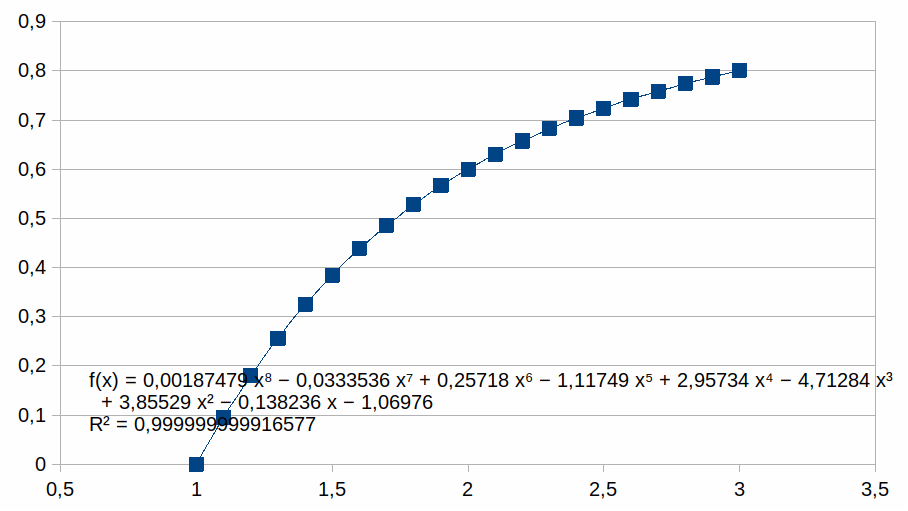
|
Terwijl
het aantal stappen die een positieve k genereren niet beperkt is,
is het aantal stappen die een negatieve k genereren kleiner.
|
0,5
|
|
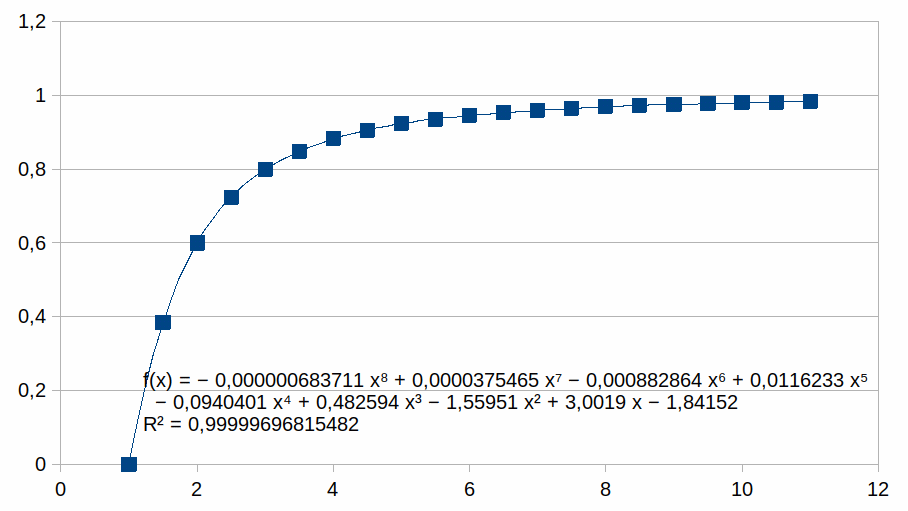
|
De meeste stappen genereren een positieve k. De symmetrie is
duidelijk in de grafiek.
|
1
|
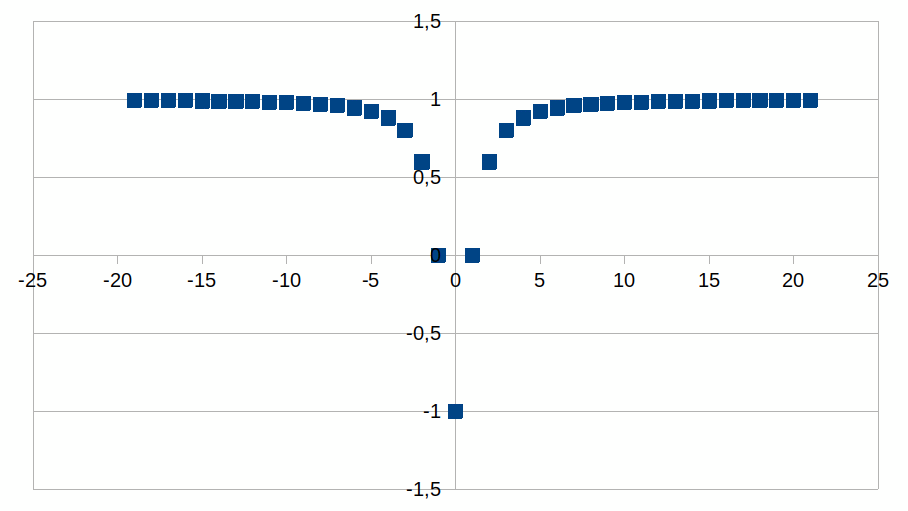
|
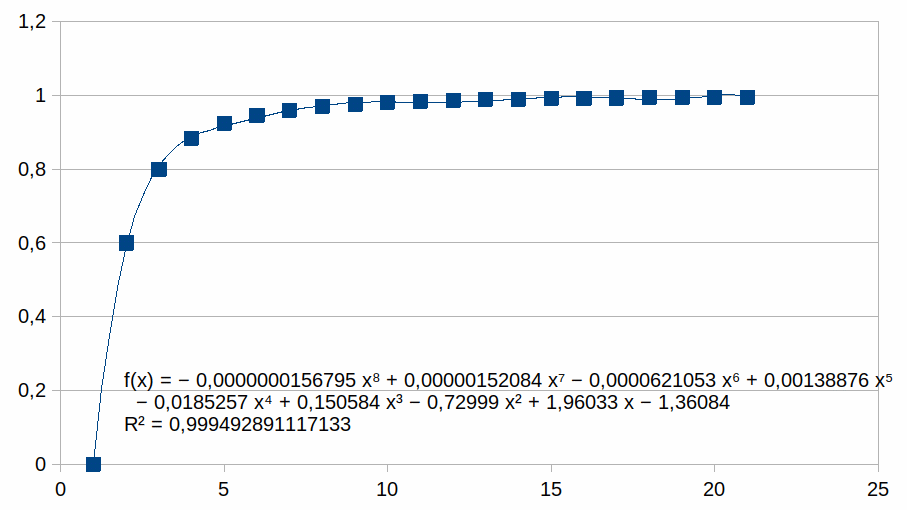
|
Symmetrische grafiek met maar één stap die een negatieve k
genereert.
Dit komt overeen met de eenheid
2Fwaargenomen/Fuitgezonden=1=z of dus een
halvering van de waargenomen frequentie (of dus een verdubbeling
van de waargenomen golflengte)
|
2
|
|
|
Symmetrische grafiek zonder negatieve k.
|
De schaal tussen twee golflengtes of frequenties z komt overeen
met een proces eigenwaarde k tussen -1 (die bereikt kan worden) en +1
(die niet bereikt kan worden). Hierdoor is het bereik van negatieve
feedback (en dus evenwicht) veel kleiner dan van positieve feedback.
De eenheid 2Fwaargenomen/Fuitgezonden=1=z is
niet anders dan een halvering van de waargenomen frequentie (of dus
een verdubbeling van de waargenomen golflengte).
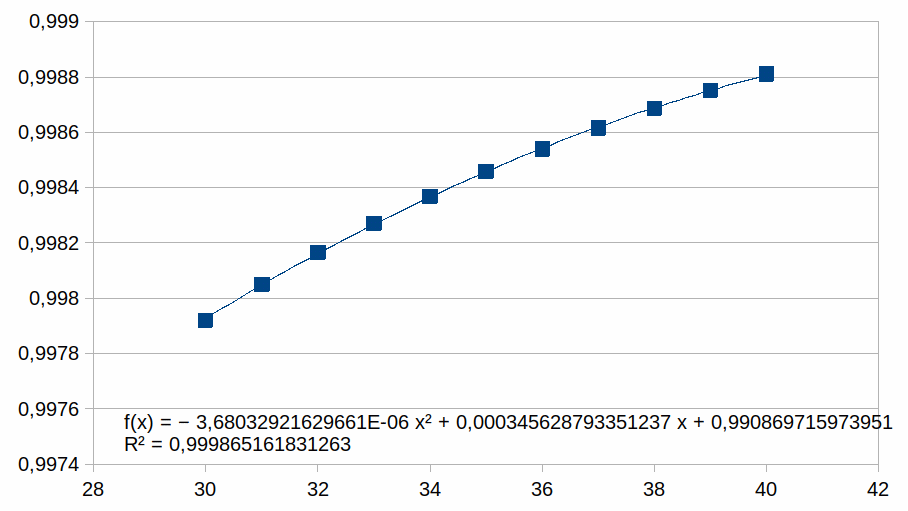
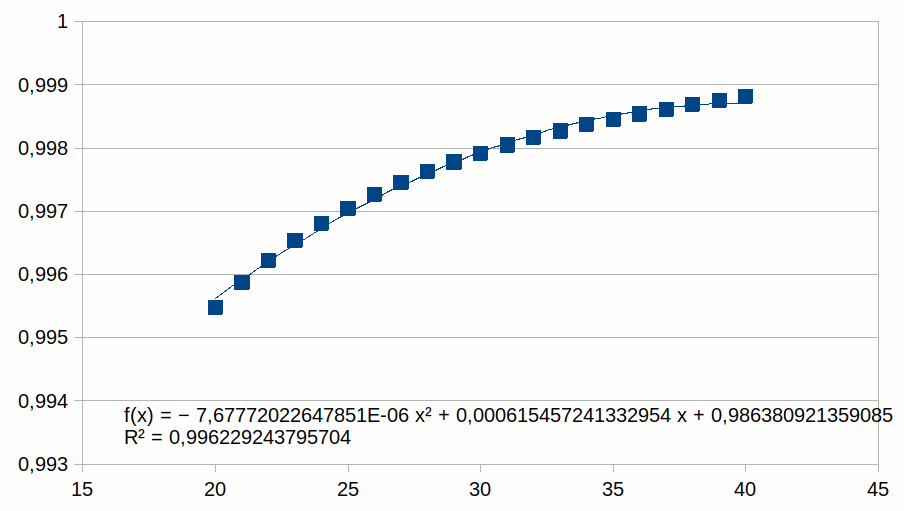
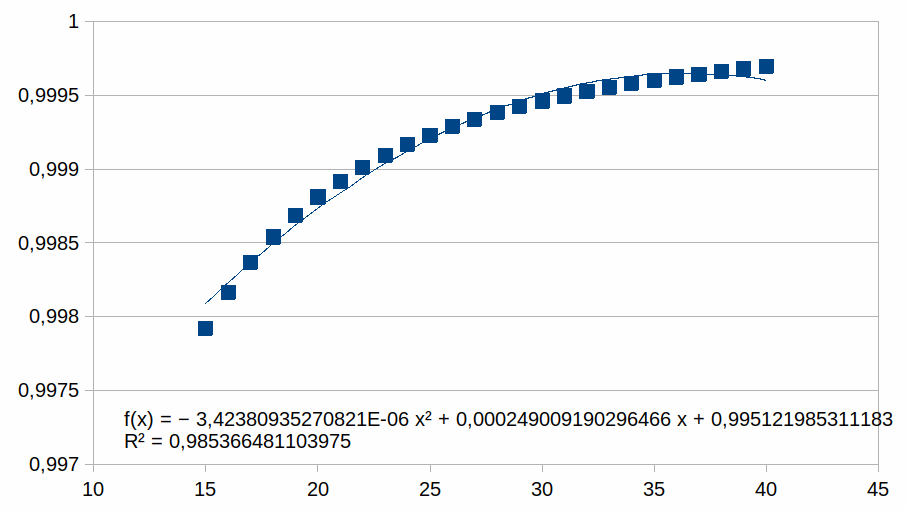
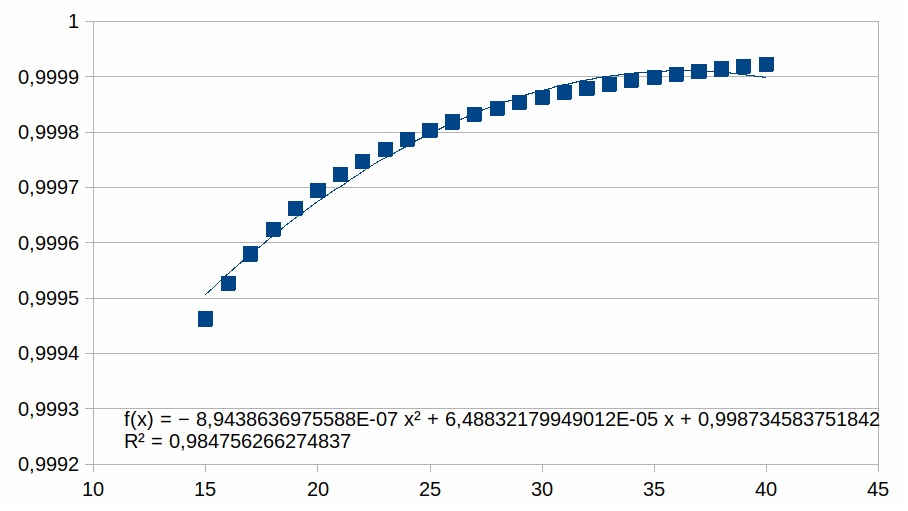
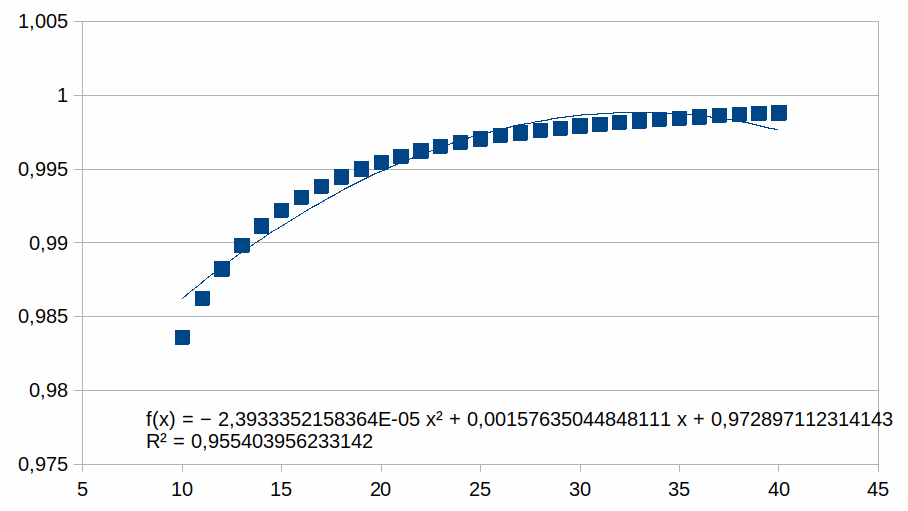
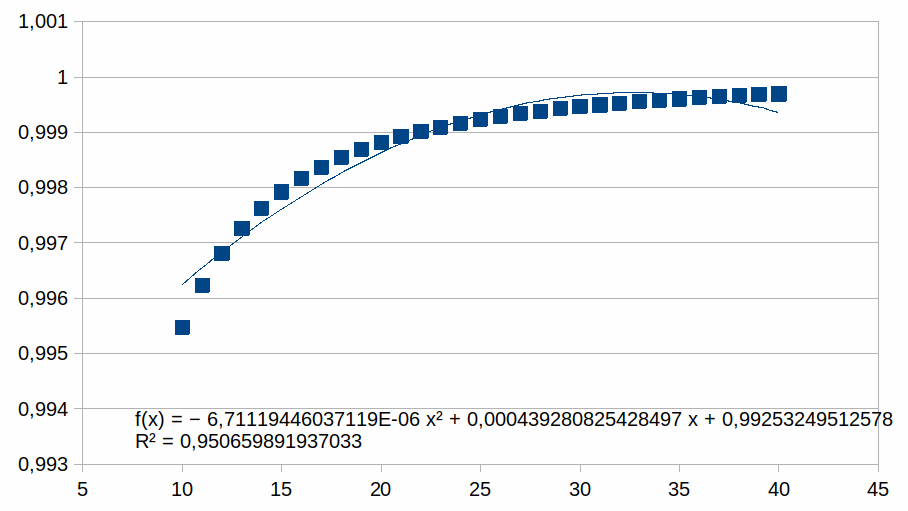
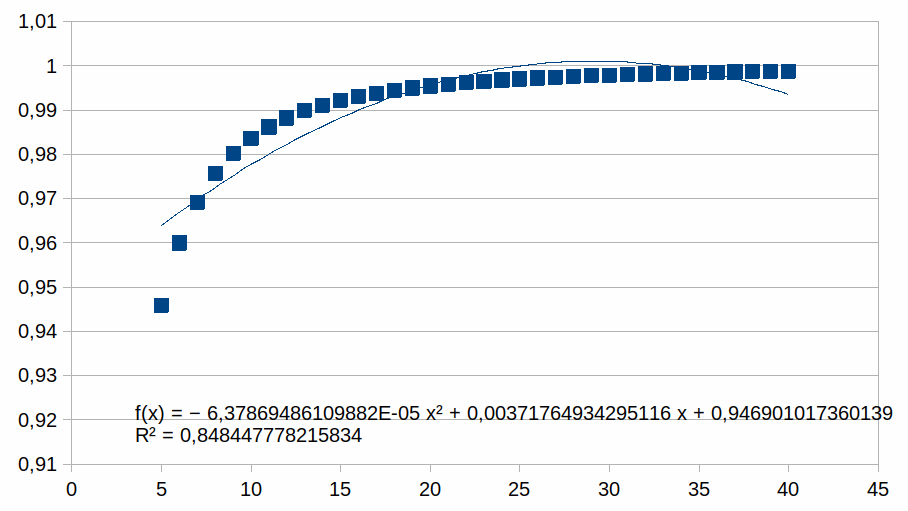
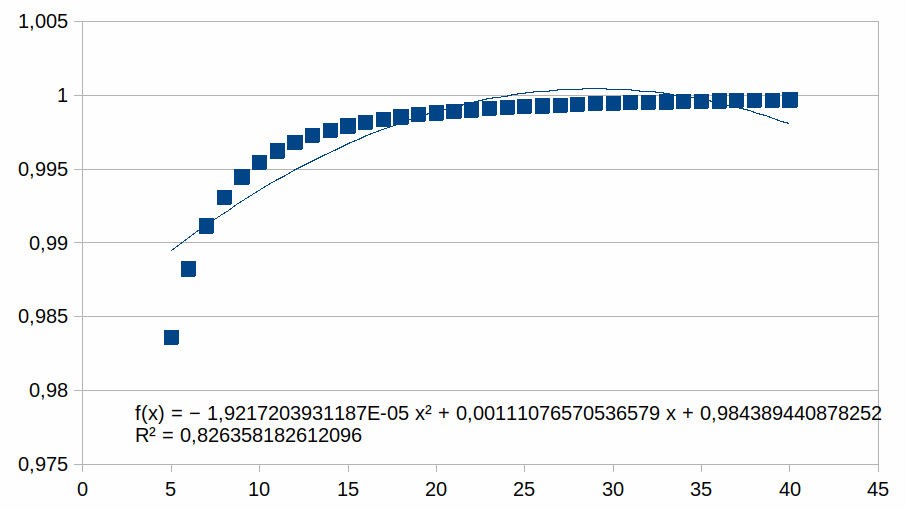
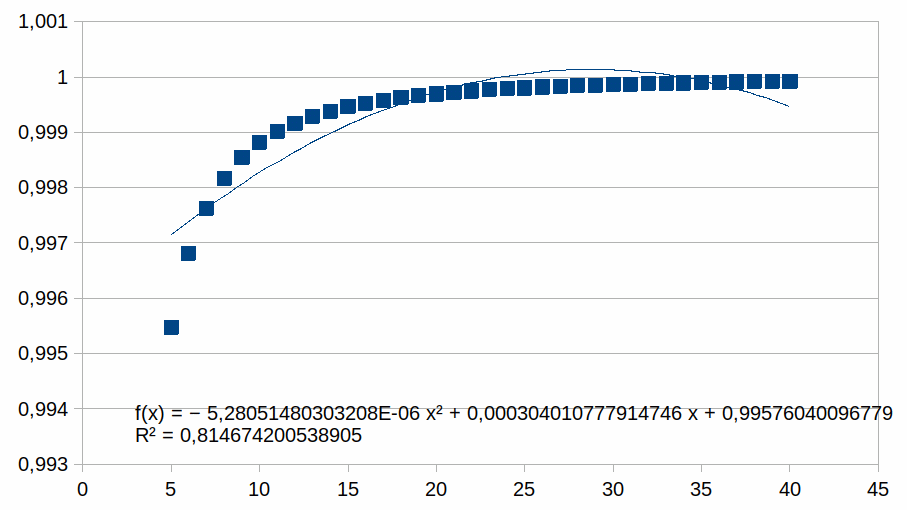
In de grafiek zijn er 40 z waarden voorgesteld. We zullen nu
grafieken tonen met enkel positieve z waarden en we benaderen deze
met een polynoom van de tweede graad (als voorbeeld, we zouden ook
een eerste graad of een andere graad kunnen gebruikt hebben). We
plotten enkel punten in een beperkt bereik bij hogere z waarden
waarmee we illustreren dat de polynoom een steeds betere benadering
is van de curve naarmate z hoger is (dat geldt dan voor gelijk welke
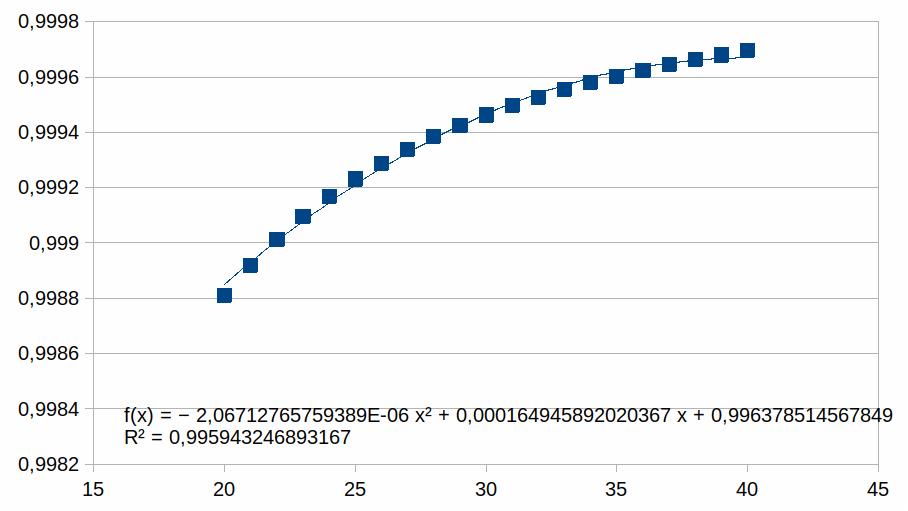
polynoom). Voor elk bereik verschalen we met een macht van 2. Dat
betekent dus dat de rij met kop 30-40 de grafiek toont voor het
bereik 30-40 in de kolom met kop 1, het bereik 60-80 in de kolom met
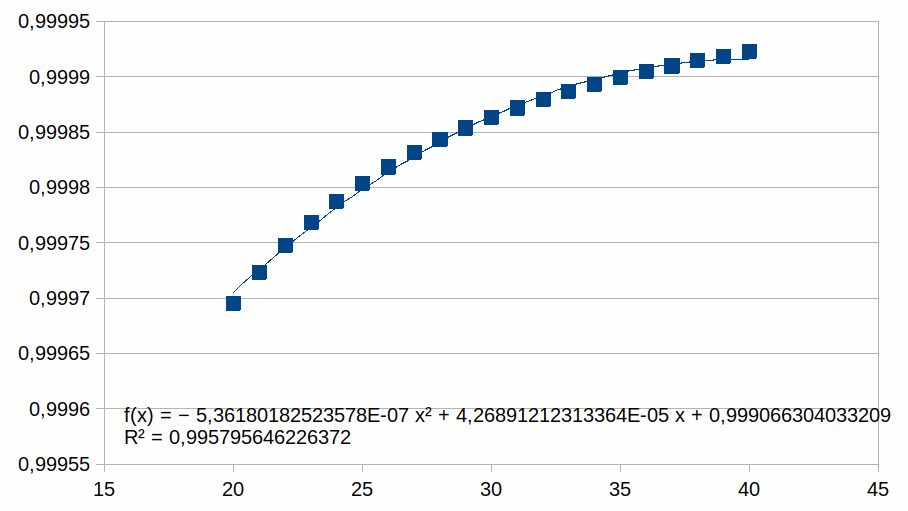
kop 2, het bereik 120-160 in de kolom met kop 4, het bereik 240-320
in de kolom met kop 8.
|
1
|
2
|
4
|
8
|
30-40
|
|
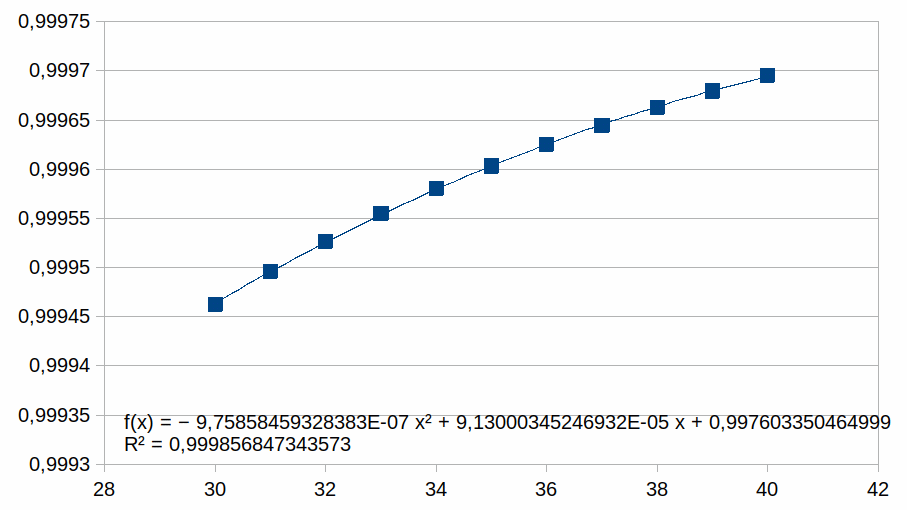
|
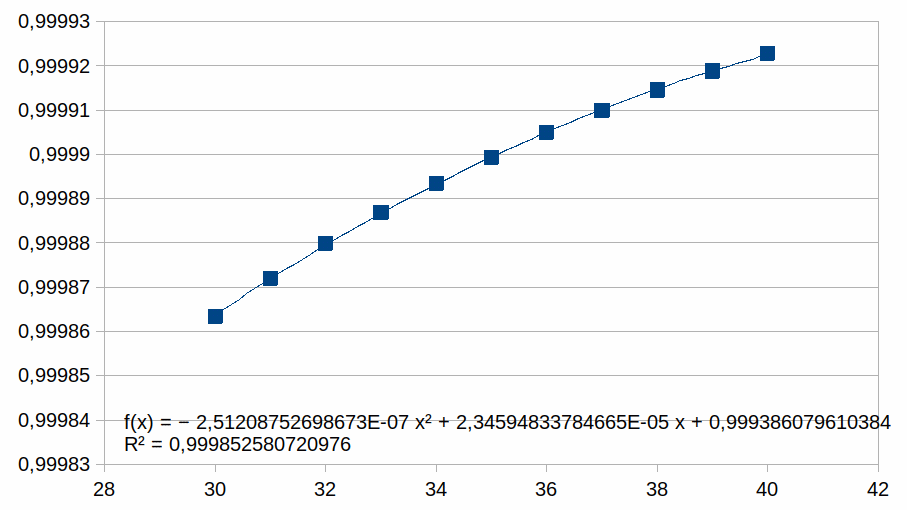
|

|
25-40
|
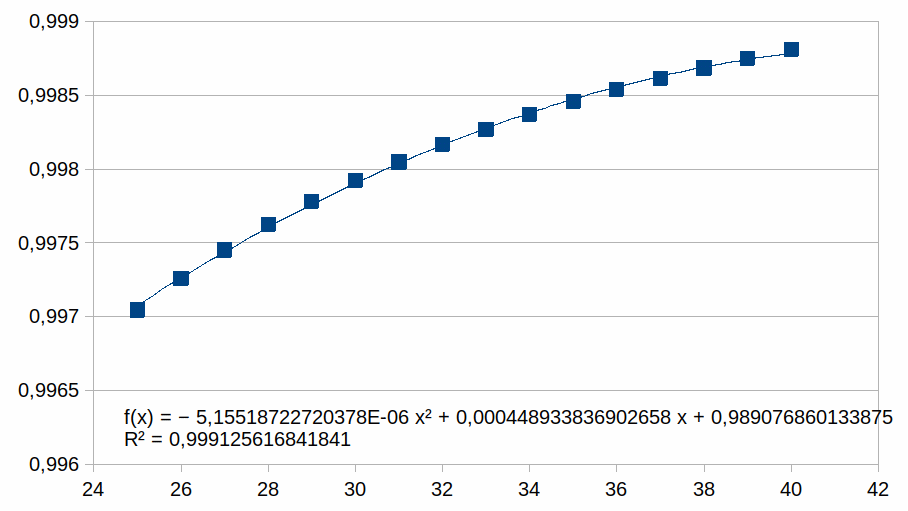
|
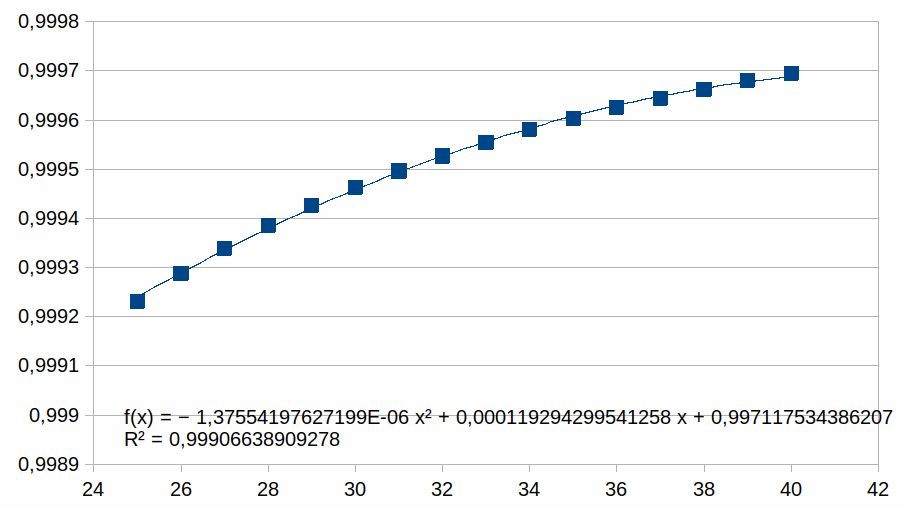
|
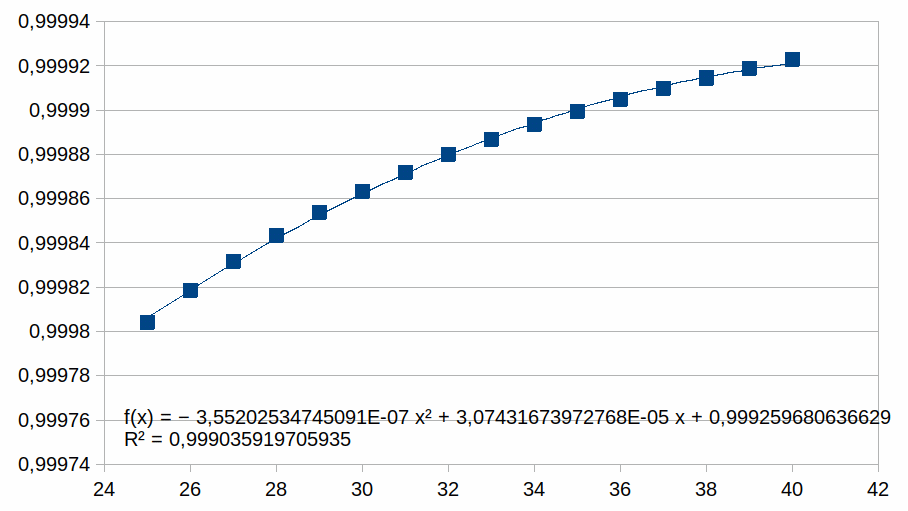
|

|
20-40
|
|
|
|

|
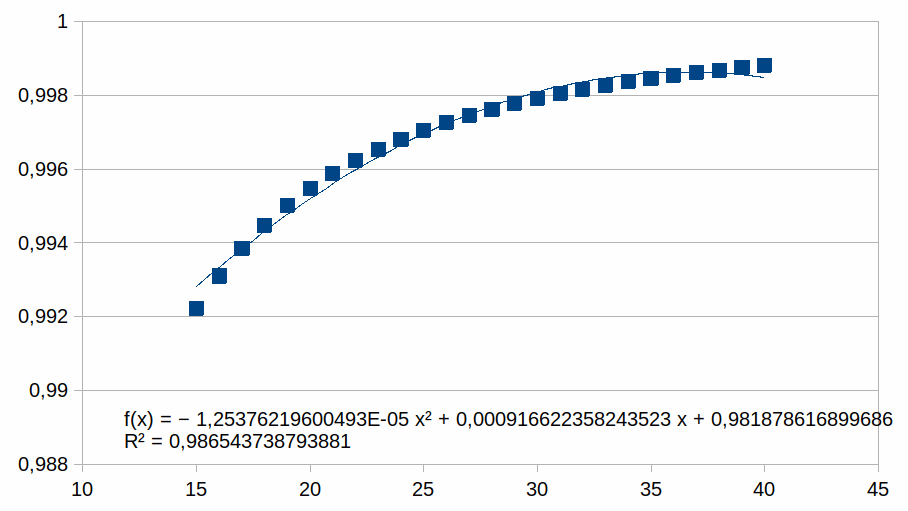
15-40
|
|
|
|

|
10-40
|
|
|

|

|
5-40
|
|
|
|

|
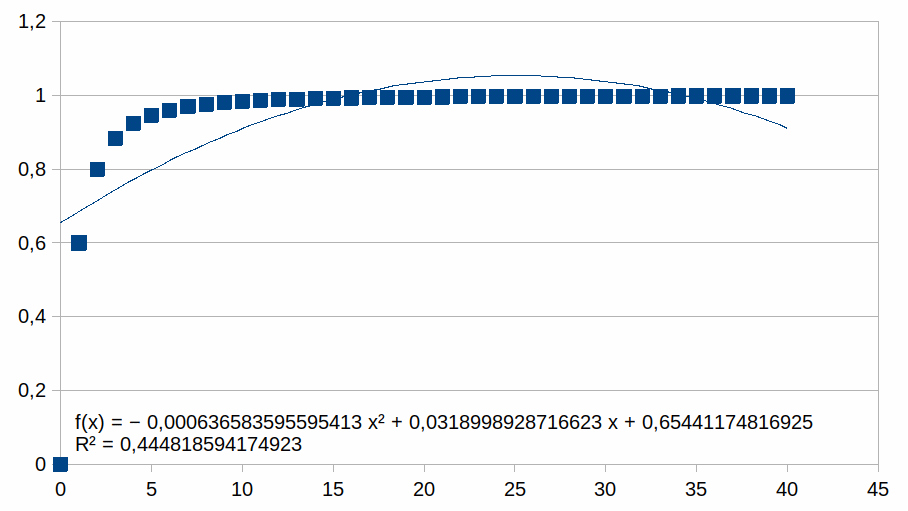
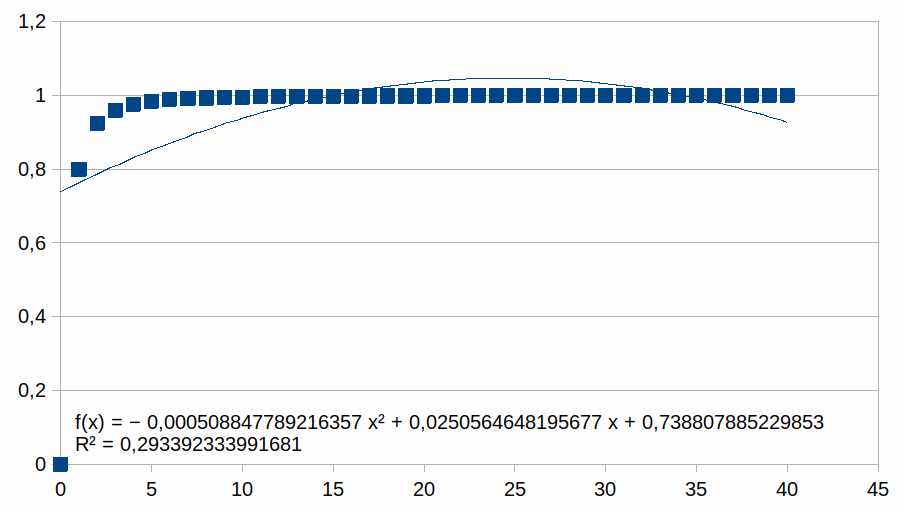
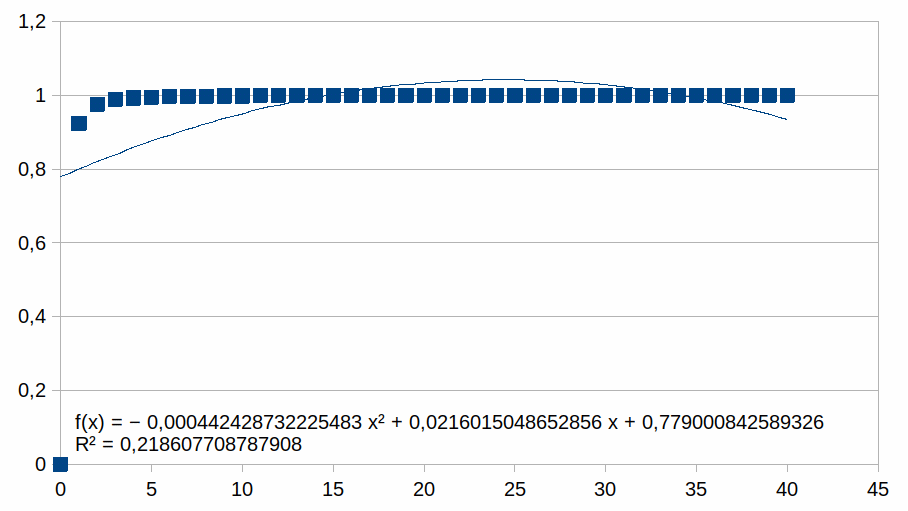
0-40
|
|
|
|

|
Hieruit volgt dat hoe korter het bereik is hoe groter de
overeenkomst met een polynoom.
Relativistisch doppler effect
Wanneer z>0 noemen we dat wat waargenomen wordt een
roodverschuiving, dan is (1+z)>1 en er is dus geen negatief
feedback proces gemodelleerd. Wanneer z<0 noemen we dat
blauwverschuiving, dan is (1+z)<1 en is er dus wel een negatief
feedback proces gemodelleerd. De asymmetrie tussen beide is
opmerkelijk en heeft gevolgen voor de interpretatie van het
relativistisch doppler effect.
Uit de veronderstelling dat een verschil van kwadraten gelijk is
aan een kwadraat zullen we nu bewijzen dat we karakteristieken uit de
relativiteitstheorie terugvinden voor de eenheid (1+z).
We hebben verondersteld dat:
(1-k)/(1+k)=(1+z)-2
(1+k)/(1-k)=(1+z)2
(1+k)1/2/(1-k)1/2=(1+z)
Het linkerlid van de gelijkheid schrijven we nu anders. We
gebruiken daartoe de bekende gelijkheid (1-k2)=(1+k)(1-k)
dus (1-k2)-1/2=(1+k)-1/2(1-k)-1/2
waarmee we gelijk
welke verhouding kunnen verschalen. Deze gelijkheid hebben we ook
toegepast om negatieve feedback en positieve feedback met
elkaar te normaliseren.
Beide leden van de vergelijking (1-k2)-1/2=(1+k)-1/2(1-k)-1/2
vermenigvuldigen we met (1+k):
(1+k)(1-k2)-1/2=(1+k)(1+k)-1/2(1-k)-1/2
(1+k)(1-k2)-1/2=(1+k)1/2(1-k)-1/2=(1+k)1/2/(1-k)1/2
en deze verhouding hebben we hierboven geïdentificeerd met (1+z).
Hieruit volgt dat
(1+k)(1-k2)-1/2=(1+z)
Wanneer we k=v/c stellen, herkennen we hierin de roodverschuiving
zoals ze moet uitgedrukt worden in de speciale
relativiteitstheorie met v=v12, een van de drie
verhoudingen uit de relatie v01+v12+v20=0
en c een constante verhouding. Er geldt dan:
z=(1+v/c)(1-v2/c2)-1/2-1. Hierin
wordt (1-v2/c2)-1/2 dan voorgesteld
als γ (die de tijdrek genoemd wordt).
Noteer dat we γ2 enkel
vanuit de veronderstelling van verhoudingen geconstrueerd
hebben als γ12γ21 rekening houdend met
alle consequenties voor commensurabiliteit.
Er geldt dus de meer expliciete vorm:
γ∼(γ12γ21)-1/2=(1/(1-v212))-1/2=(1/(1-v221))-1/2=(1-(n1-n2)2/(n1+n2)2)-1/2.
Dus: γ∼γ12γ211/2=((n1+n2)/2)/(n1n2)1/2,
dit is de verhouding van het rekenkundig gemiddelde van n1
en n2 (de teller) tot het geometrisch gemiddelde van n1
en n2 (de noemer).
Zoals gewoonlijk in de
relativiteitstheorie, kunnen we ook een benadering construeren voor
kleine k.
Uit (1-k)/(1+k)=(1+z)-2 volgt (1-2k/(1+k))=(1+z)-2
en dus (1-2k/(1+k))1/2=(1+z)-1. Nu kunnen we de
uitdrukking (1-2k/(1+k))1/2 in zijn binomiale expansie
schrijven. De binomiale expansie van (a+b)n wordt gegeven
door an+(n/1!)an-1b+(n(n-1)/2!)an-2b2+...
dus de binomiale expansie van (1-2k/(1+k))1/2 wordt
gegeven door 11/2+(1/2)11/2-1(-2k/(1+k))
+((1/2)(-1/2)/2!)11/2-2(-2k/(1+k))2+...
en als k zeer klein is dan kunnen de derde term en alle volgende als
verwaarloosbaar beschouwd worden en dus kunnen we de factor (1+z)-1
schrijven als 1-k/(1+k) of dus 1/(1+k). Dus 1/(1+z)=1/(1+k).
Hieruit volgt z=k in dit geval. Dus voor zeer kleine k is
((1+k)/(1-k))-2 een benadering voor 1+z, en dus k een
benadering voor z.
Hierdoor is duidelijk dat z=(1+v/c)(1-v2/c2)-1/2-1,
evenals k, beschouwd kan worden als de karakterisering van een
feedback proces met z als eigenwaarde zoals ook k een eigenwaarde is.
Hierbij blijkt dat er meer mogelijke processen leiden tot begrensde
toename dan er processen zijn die naar een evenwicht evolueren. Het
zijn de processen die leiden tot begrensde toename van sporen die “de
populaties” of “de
intensiteit van de buffers” zo groot kunnen maken dat er nieuwe
coördinaties ontstaan en daardoor dus nieuwe soorten entiteiten.
We hebben zowel positieve
als negatieve feedback onderzocht als het begrensd patroon
(1-l)/l (een verhouding (1-k)/(1+k) is altijd te schrijven als een
(1-l)/l voor een l=(1+k)/2). Nu komt daar nog een patroon bij dat ook
enkel maar een schaaleffect heeft en begrensd is.
Het klassieke doppler effect
Het is goed om zich eens de klassieke behandeling te herinneren
die ontstond bij de beschrijving van geluidsgolven, waardoor we
duidelijk kunnen zien hoe dat verschilt van onze eigen afleiding die
volledig relativistisch is (geen enkel referentieframe of verhouding
is speciaal in de relatie v01+v12+v20=0).
Het klassieke doppler effect is in inderdaad niet relativistisch: het
effect van een bewegende bron is anders dan het effect van een
bewegende waarnemer, aan beide moeten we een snelheid toekennen. Maar
om die bekende behandeling te kunnen opbouwen hebben we wel een
geometrische interpretatie nodig: het is een effect in de
driediemensionale ruimte.
We interpreteren z=k voor kleine waarden nu niet meer als
een eigenwaarde, maar als v/c met v de snelheid van een ver
verwijderde entiteit die een bekend licht uitstraalt met een goed
gedefinieerd spectrum en c de snelheid van licht. z=v/c wordt dan een
roodverschuiving (toename van golflengte) genoemd als z>0, en een
blauwverschuiving (afname van golflengte) als z<0. We zullen
aangeven wanneer deze afleiding in het geval van licht ons ertoe
dwingt om 1/c als eenheid te beschouwen van een verhouding die
een intensiteit v kan krijgen.
Een stilstaande lichtbron B produceert een lichtflits met
frequentie FB en met een constante golflengte GB.
Het licht heeft de constante snelheid c. Het laboratorium L
verwijdert zich van de lichtbron met snelheid u. Op tijd TB
heeft het golffront een afstand afgelegd van GB=cTL
en het laboratorium een afstand uTL. De totale afstand van
het golffront tot de bron is dan het verschil van beide (het laatste
beetje golf van de flits heeft het laboratorium nog niet bereikt):
cTL-uTL en die is gelijk aan de golflengte GB
geobserveerd in het laboratorium. Deze is per definitie niet anders
dan GB=cTB. Er geldt dus:
cTB=cTL-uTL=(c-u)TL
Tijden zijn de invers van frequentie dus
c/FB=(c-u)/FL
FL=FB((c-u)/c): dus de waargenomen
frequentie is kleiner dan de uitgezonden frequentie.
Met eenzelfde redenering komen we tot de conclusie dat als het
laboratorium L dichter bij de lichtbron komt met snelheid u, dat de
waargenomen frequentie groter zal zijn dan de uitgezonden frequentie,
met de formule FL=FB((c+u)/c). Het is
merkwaardig dat hier een term staat, namelijk (c+u), die voor licht
fysisch onmogelijk te realiseren is zoals dat door veel experimenten
bevestigd werd. Maar die term is deel van een verhouding (c+u)/c en
dat kunnen we ook schrijven als (1+u/c) wat aantoont dat c hier de
functie heeft van een eenheid en u een intensiteit.
Voor alle mogelijke combinaties, die nu niet expliciet uitgewerkt
worden, kunnen we dan de volgende relaties afleiden, waarbij v de
snelheid is van de bron en u de snelheid van het laboratorium, beide
snelheden kunnen verschillen.
|
Stilstaand
laboratorium
|
Laboratorium
beweegt naar de bron
|
Laboratorium
beweegt van de bron weg
|
Stilstaande
bron
|
FL=FB
|
FL=FB((c+u)/c)
|
FL=FB((c-u)/c)
|
Bron
beweegt naar het laboratorium
|
FL=FB(c/(c-v))
|
FL=FB((c+u)/(c-v))
|
FL=FB((c-u)/(c-v))
|
Bron
beweegt van het laboratorium weg
|
FL=FB(c/(c+v))
|
FL=FB((c+u)/(c+v))
|
FL=FB((c-u)/(c+v))
|
Dit zijn relaties in een Euclidische
ruimte (drie dimensies met absolute tijd) in tegenstelling met de
relaties die wij onderzochten die verwijzen naar een Minkowski
ruimte (vier dimensies).
Bespreking
De interpretatie die we hier uitgewerkt hebben maakt duidelijk dat
er minstens een procesevenwicht aan de basis ligt van een toename of
afname van de frequentie van een repetitief proces als dat aanwezig
zou zijn. We kunnen “tijd” dus vervangen door “periode” of
“stap” en hiermee laten we de veronderstelling “dat tijd
absoluut is” volledig varen. We proberen de waarnemingen dus te
verklaren door processen te veronderstellen waarvan de eigenwaarde
kan veranderen (en dus zonder dat we hiervoor geometrische of
ruimtelijke intuïties nodig hebben). De verandering van eigenwaarde
leidt tot een verandering van de halverings”tijd” of
verdubbelings”tijd” en dat kunnen we tellen omdat dit sporen
achterlaat. De interactie van die procestijden kunnen we
anticiperen door de interactie van processen op aarde als model te
gebruiken (bijvoorbeeld met de inzichten van de systeem
dynamica of de dynamica van populaties
van soorten die met elkaar interageren en die de eigenwaarde van
hun processen daarvoor “op elkaar afstemmen”). Het verklaren van
waarnemingen aan objecten in de kosmische ruimte zou daardoor
mogelijk worden in termen die we op aarde herkennen.
We hebben gezien dat, als de eenheid e van de verhouding (het
getal) v verschilt van 1, de Lorentz boost geen procesevenwicht met
drie factoren beschrijft maar een
grens aan de waarnemingsresolutie: een van de drie
verhoudingen is enkel als nul waarneembaar (ons voorbeeld gebruikte
hiervoor v12). Dat kunnen we interpreteren dat de inverse
verhouding zeer groot is en onwaarneembaar groter en invariant (zoals
we nu enkel veronderstellen voor de lichtsnelheid). Dat is echter een
universeel gegeven (en dus niet enkel toepasbaar voor
elektromagnetische straling) omdat dit het gevolg is van gelijk welke
waarneming van getallen ni, getallen die sporen zijn van
een meting of waarneming: we nemen altijd iets waar, er is altijd een
getal verschillend van nul. Het is dat getal dat we als eenheid
van de gemeten verhoudingen kunnen gebruiken en zo’n getal hoeven
we niet als de “lichtsnelheid in vacuum” te interpreteren, het is
een van de vele mogelijke interpretaties van verhoudingen vij en
de
meest universele constructie ervan
is e2=1/(1±z)2.
Met verschillende eenheden 1/(1±zi)2
kunnen
we dan een tralie opspannen, op voorwaarde dat we de 1±zi
relatief priem kiezen. Elke
(1±zi)-2
beelden we dan af op een AND-atoom
en interpreteren we als de eenheid van een toestand die alle andere
uitsluit en die een intensiteit kan hebben. Hoe meer zo’n eenheden
nodig geacht worden, hoe meer onderscheidingen moeten verondersteld
worden en elke onderscheiding is te
implementeren als een golf vanuit de veronderstelling dat we de
wortels van 1 gebruiken (die een vorm zijn van 1±zi
met zi
een complex getal). Universa die
hetzelfde kunnen uitdrukken vinden we dus wanneer we
een verschaling vinden tussen eenheden die
dezelfde tralie genereren. Dat betekent dus dat we andere
intensiteiten (van
die eenheden) zullen vinden. Zo we willen kunnen we die als
coördinaten
interpreteren en we hoeven dit
niet ruimtelijk te zien (we doen dit enkel wanneer we ons de diepe
kosmos proberen voor te stellen door gebruik te maken van het
spoor “ruimtelijke afstand” dat gecreëerd is door een
ongekend proces en dat ons
in staat stelt om van een “lichtsnelheid”
te spreken).
De relatie (1+k)(1-k2)-1/2=(1+z) is dus van
niet te onderschatten belang.
(1+k)(1-k2)-1/2=(1+z) is een relatie tussen
de dubbelgetallen (1+k) en (1+z) waarbij k en z zowel negatief als
positief kunnen zijn. De relatie is onafhankelijk van de
interpretatie ervan en we kunnen dus verschillende interpretaties
geven aan dat patroon. We moeten dan in staat zijn om die
interpretaties met hun opbouwende veronderstellingen onder ogen te
zien. In het algemeen geval beschrijft de vergelijking de relatie van
eigenwaarde k van een proces en een verhouding z die we interpreteren
als een aspect van abstracte golfverschijnselen (frequenties van
(on)zekerheid).
Er zijn al verschillende
“roodverschuivingen” beschreven: de “roodverschuiving” die
gerelateerd is aan een lichtbron die zich van ons verwijdert (of
blauwverschuiving als die naar ons toe komt), de “roodverschuiving”
die we interpreteren als een voortdurende expansie van het
ruimtelijk universum zonder centraal punt, en de “roodverschuiving”
in de buurt van een grote massa die duidelijk verband houdt met
tijdrek (tijddilatatie) in die omgeving. Zij drukken de
onvermijdelijkheid uit van een laatst toegevoegde onderscheiding op
de (onvermijdelijk altijd) laagste frequentie, de laagste
“veelvuldigheid van zekerheid” en daar verbinden
we een hypothetisch verleden gebeurtenis aan als we het heden
modelleren als de voldoende voorwaarde voor het verleden, maar daar
verbinden we een hypothetisch toekomstige gebeurtenis aan als we het
heden modelleren als de noodzakelijke voorwaarde voor de toekomst.
Bijvoorbeeld: een noodzakelijke veronderstelling voor het
relativistisch doppler effect voor straling in de ruimte is dat een
“ver” verwijderde entiteit een bekend licht uitstraalt met een
goed gedefinieerd spectrum. We interpreteren dan dat die informatie
in het verleden gegenereerd werd en ons nu pas bereikt omdat de
energetische drager daar zolang over gedaan heeft. We gaan ervan uit
dat we die informatie herkennen vanuit de processen die op aarde
mogelijks uit te voeren zijn. We veronderstellen dus dat die (“daar”
en “toen” actieve) entiteiten een elektromagnetische straling
genereren met bekende frequenties zoals ze dat ook op aarde doen. We
gaan er dan van uit (1) dat die processen onveranderd zijn in een
ruimte die ver van ons verwijderd is (bijvoorbeeld: een foton werd
“daar” (of “toen”) op dezelfde manier gegenereerd) en (2) dat
de straling onderweg niet door nog onbekende factoren beïnvloed
wordt. Dit zijn heel ingrijpende veronderstelling. Inderdaad kennen
we hier op aarde zoiets als (licht)reflectie en (licht)breking,
effecten die verklaard worden door te veronderstellen dat de
(licht)snelheid afhankelijk is van het materiaal (de
wet van Snellius). Die optische effecten (denk aan de
verschillende soorten lenzen die daardoor kunnen gemaakt worden)
kennen we vanuit onze onmiddellijke omgeving, maar kennen we die voor
“materialen in de kosmos” die hypothetisch aanwezig kunnen zijn
op een afstand die enkel door golfverschijnselen waarneembaar is (en
dus met een zekere frequentie van (on)zekerheid)? Moeten die golven
dan elektromagnetische golven zijn? We onderscheiden al gravitatie
lenzen, zijn er misschien nog andere processen? Wat met processen die
“in de diepe ruimte” (“in dat ver verleden”) andere golven
zouden genereren (frequenties van (on)zekerheid) terwijl ze dat
(“nu”) op aarde niet doen? Is het nuttig om die hypothesen te
genereren?
We kunnen in elk geval besluiten dat we “roodverschuiving”
en “blauwverschuiving” waarnemen wanneer hypothetische entiteiten
veranderen van processen waarvan ze deel uitmaken (bijvoorbeeld door
zelf te veranderen). We kunnen dat waarnemen als die processen sporen
achterlaten die repetitief zijn en dus herkend worden. De
densiteit van de gebeurtenissen die we herkennen verandert,
en dan is het alsof de tijd trager of sneller loopt vergeleken met
processen die we “dezelfde” noemen als <<nu>>
<<op aarde>>. Op
het eerste zicht moeten we dikwijls besluiten dat de tijd <<nu>>
<<op aarde>> “sneller
loopt”. Vanuit ons inzicht in processen hebben we begrepen
dat dit een verwarrende uitleg is. Het is veel correcter om te zeggen
dat sommige processen enkel kunnen beschreven worden in een
onderscheidingen universum dat groot genoeg is, een universum dat het
gepaste aantal toestanden heeft (“de geschikte densiteit”), dat
is een meer correcte uitleg die geen verwarring creëert over wat
bedoeld wordt met “snelheid”, snelheid is een densiteit van
toestanden. In de veronderstelling dat we
enkel onze interpretatie van processen in de diepe kosmos kunnen
laten afhangen van
waarnemingen van roodverschuivingen,
dan moeten we dus meerdere
hypothesen in overweging nemen dan
bijvoorbeeld enkel de expansie van het universum en dat zijn we volop
aan het doen door daar ook gravitatie bij te betrekken. De
hypothese van expansie kan zinvol zijn, maar het is ook mogelijk dat
een deel van de roodverschuiving verklaard moet worden doordat de
entiteiten die de bron zijn van het licht andere processen doorlopen
die we <<nu>> en <<op
aarde>> niet kunnen simuleren (bijvoorbeeld omdat we de
gravitatie in ons eigen zonnestelsel niet
kunnen vermijden). Hierdoor lijken
de hypothetische entiteiten <<andere
entiteiten>> te zijn die onderhevig zijn aan andere wetten,
minstens een andere klok. Het is immers mogelijk die verandering
te interpreteren als veroorzaakt
door een entiteit die deel
uitmaakt van een ander proces (met een andere processtap en andere
toestanden die elkaar uitsluiten) dan de processen die we enkel
herkennen op aarde en die onmogelijk op aarde zouden kunnen
verwezenlijkt worden. We hebben die hypothese aanvaardbaar gemaakt
omdat we “tijdrek”
kunnen waarnemen aan veel
processen op aarde die een surplus genereren (emissie die dus
niet functioneel is voor de klok van het proces), bovenop de emissie
van aspecten en entiteiten die de klok zelf karakteriseren. Processen
die zeer veel sporen achterlaten genereren de mogelijkheid dat er
nieuwe soorten ontstaan omdat er coördinatie kan waargenomen worden
bij die sporen. Wat kunnen die soorten dan zijn?
De processen die we waarnemen in
die verste entiteiten interpreteren we als sporen van een ver
verleden dat we als hypothese kunnen construeren, hypothese
die een noodzakelijke voorwaarde moet zijn voor onze werkelijkheid nu
(indien niet…, dan niet…) (dit is de definitie van verleden).
We zien dan
in straling hoe nieuwe soorten ontstaan zijn in het verleden en die
soorten kunnen we proberen te karakteriseren met hun eigen klok.
De werkelijkheid is hoe dan ook een
“indien …, dan …” constructie, dus het verleden evenzeer. Het
zou dus kunnen zijn dat de hypothese van “levende interagerende
structuren” zinvol is <<in een verleden universum>>,
structuren die het patroon van
structuren in een ecologie op aarde vertonen (interageren,
ontstaan
en verdwijnen) en die dus gelijkaardig zijn. We kunnen ze als
zodanig construeren enkel gebaseerd op het waarnemen van abstracte
golven (frequenties van (on)zekerheid) omdat ze sporen nalaten
die cyclisch voorkomen. Golven zijn ook een
fysisch te implementeren interpretatie van onderscheidingen en we
hebben bewezen dat, als we gelijk welke (dus willekeurige)
repetitieve processen gebruiken, we een voldoende onafhankelijkheid
genereren om tralies op te bouwen waarmee we hypothetische entiteiten
kunnen modelleren, ook entiteiten die kwantumgedrag vertonen. Elke
agens is daartoe op een of andere manier in staat.
Er liggen dus massa's fysische implementaties voor het grijpen om
het ontstaan van nieuwe soorten te onderzoeken en dat zal geen enkele
ontwerper verbazen.