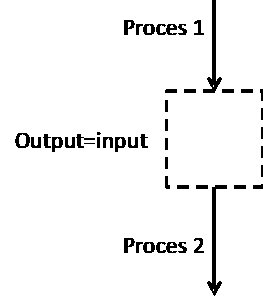
Dit is het duale van het “black box” schema:
Systeem dynamica is een praktische toepassing van cybernetische inzichten en is in parallel met de cybernetica in de tweede helft van de twintigste eeuw ontstaan (geïntroduceerd door Jay Forrester). De ontwikkeling werd slechts mogelijk doordat computers steeds performanter en toegankelijker werden en gebruikt werden om praktische problemen te simuleren in plaats van deterministisch te berekenen.
In de syteem dynamica maakt men (computer)simulaties met behulp van twee basis componenten: buffers (of “niveaus”, in het Engels “stocks” en ook “levels”) en snelheid (mate van verandering, in het Engels “rate” en ook “flow”). Buffers zijn input en output van processen. Die processen hebben een zekere processnelheid. De intensiteit van de buffers kan toenemen of afnemen: op een bepaald moment in de tijd hebben ze een bepaalde intensiteit, minimaal een ordinale waarde in de simulatie, die soms vertaald kan worden als een kwantitatieve waarde in de computersimulaties. De intensiteit verandert door enerzijds een proces dat de intensiteit doet toenemen, anderzijds door een proces dat de intensiteit doet afnemen. Het samenspel van beide processen resulteert in een bepaalde intensiteit van de buffer. Twee buffers worden met elkaar verbonden door processen die verder niet gekend zijn maar die kunnen gevolgd worden door de mate van verandering te registreren die beide buffers koppelt. Op die manier kan men gesloten lussen modelleren en interagerende processen met verschillende snelheden als één geheel samen bestuderen.
De snelheid van sommige processen is stuurbaar, de snelheid van andere processen moet als zodanig aanvaard worden. De stuurbare processen zijn regelbaar door de intensiteit van een buffer A te veranderen, intensiteit die men afhankelijk maakt van een regelbare buffer B, zoals men het debiet in een vloeistofleiding kan veranderen door de grootte (intensiteit) van de doorsnede van de leiding te veranderen waardoor de stroomsnelheid verandert. Dit kan men doen zowel op de instroom (input) van buffer A als op de uitstroom (output) van buffer A. Hier zijn dus voor één resultaat-buffer, namelijk A, de relatie met twee buffers te regelen, namelijk de buffers B en C. Dit is typisch voor materiaalprocessen of energieprocessen. In sommige modellen zal men de regelbare input en output dan ook met het symbool van een kraantje voorstellen. Regelen kan men echter niet alleen op die manier, maar voornamelijk door de relaties (en dus de processen) tussen de buffers te wijzigen (bijvoorbeeld processen wegnemen of processen toevoegen zelfs voor een niet veranderend aantal buffers). Dit is typisch voor informatieprocessen. Als men op een bepaald moment informatie krijgt over de toestand van het gemodelleerd systeem, dan kan men bepaalde regelingen anticiperen. Bijvoorbeeld: als men de verdubbelingstijd kent van een buffer in een positieve feedback proces dan moet men niet wachten tot men aan de buffer vaststelt dat hij een bepaalde waarde heeft om actie te ondernemen, maar kan men die regeling nu al anticiperen.
In het haakformalisme hebben we de processnelheden als de verschillende eigenwaarden k van spontane processen gemodelleerd. De globale tijdstap is dan de meest langdurige stap die één toestandsverandering geeft in het totale (“genormaliseerde”) systeem. De normalisatie genereert de eenheid (x-x0). De kwantitatieve relaties die door de modellering van positieve en negatieve feedback gecreëerd worden zijn de intensiteiten van één verschil dat een verschil maakt, namelijk (x-x0). De structuur (x-x0) is eigen aan een transformatie en is dus de eenheid van de buffer die de transformatie meemaakt (die de output is van de ene transformatie en de input van de andere transformatie). Een vectorbenadering zal voor elk verschil dat een verschil maakt een andere vectorcomponent (een andere eenheid) gebruiken en aan elke vectorcomponent zal een eigen relevante tijdstap kunnen toegewezen worden. De verschillen in waarnemingsresolutie leiden ertoe dat discontinue veranderingen kunnen optreden (“indien..., dan..., zoniet...”): als een bepaalde grens overschreden is zal een exponentieel toenemende of afnemende verandering de relaties tussen de componenten van de vectoren grondig kunnen wijzigen.
Een manier om systemen te modelleren is om te proberen om een “causal loop diagram” te maken. (Zoals dikwijls, is die naamgeving historisch ontstaan en dus beladen met connotaties die voor de pioniers van de systeem dynamica vanzelfsprekend waren. De symmetrie in de uitspraken in onderstaande tabel zal dit duidelijk maken.) Het is een diagram met enkel buffers en processen met een processnelheid. Ze wisselen elkaar af en zo kunnen feedback lussen gemaakt worden. Het meest primitieve diagram is dus:

Dit
is het duale van het “black box” schema:
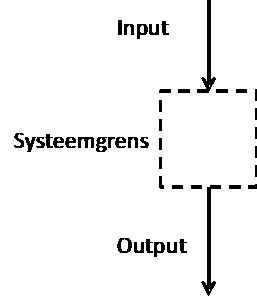
Dit
zorgt natuurlijk voor verwarring indien beide schema's gemengd
worden.
Niveaus zijn hoeveelheden, intensiteiten, afmetingen enz …, zijn dus accumulaties van iets, ze hebben een waarde, zelfs als er geen verandering verondersteld wordt. Snelheden verduidelijken hoe ordinale waarderingen gerelateerd zijn tussen twee niveaus. Een grotere snelheid overbrugt een groter niveauverschil. Een snelheid heeft geen waarde als er geen verandering verondersteld wordt, de accumulatie behoudt zijn waarde. Hier zien we een nieuwe bron van mogelijke verwarring opduiken, want een snelheid kan zelf veranderen afhankelijk van een accumulatie. Stop de verandering van snelheid, dan stopt de snelheid niet. Stop de snelheid, dan stopt ook de verandering van snelheid. Beide relaties kunnen voorkomen in één diagram en we moeten snelheid (verschil tussen twee stappen) en versnelling (verschil tussen het verschil tussen twee stappen) van elkaar kunnen onderscheiden. Dat kan door expliciet ook snelheid (eigenwaarde) als een buffer te modelleren.
Omdat er slechts twee soorten feedback mogelijk zijn, kunnen die relaties worden gelabeld met een binaire code (bijvoorbeeld + versus - of groen versus rood, of s versus o, of volle lijn versus gestippelde lijn etc ...).
Code |
Relatie |
Gelijkwaardige uitdrukking van dezelfde relatie |
Voorbeeld van regeling |
Equivalent voorbeeld van regeling |
+A +B |
Het verhogen van A komt overeen met het verhogen van B Het verhogen van B komt overeen met het verhogen van A |
Het verlagen van A komt overeen met het verlagen van B Het verlagen van B komt overeen met het verlagen van A |
Het verhogen (verlagen) van geboorten doet de bevolking stijgen (dalen) in vergelijking met ongewijzigde geboorten Het verhogen (verlagen) van de bevolking verhoogt (verlaagt) de geboorten in vergelijking met een ongewijzigde bevolking |
Bij toenemende (dalende) overleving stijgt (daalt) de bevolking in vergelijking met ongewijzigde overleving Bij toenemende (dalende) bevolking stijgt (daalt) het aantal overlevers in vergelijking met ongewijzigde bevolking |
+A -B |
Het verhogen van A komt overeen met het verlagen van B Het verhogen van B komt overeen met het verlagen van A |
Het verlagen van A komt overeen met het verhogen van B Het verlagen van B komt overeen met het verhogen van A |
Het verhogen (verlagen) van de sterfte doet de bevolking afnemen (toenemen) in vergelijking met ongewijzigde sterfte |
Bij toenemende (dalende) bevolking daalt (stijgt) de sterfte in vergelijking met ongewijzigde bevolking |
De code (eerste kolom) geeft dus de relatieve verhouding van verandering tussen de waargenomen intensiteiten van de twee gerelateerde niveaus. Het diagram is derhalve zinvol, zelfs als de niveaus alleen gedefinieerd zijn op een ordinaal niveau, en zelfs als het niet bekend hoe de intensiteiten van de twee niveaus aan elkaar gerelateerd zijn in termen van andere (bijvoorbeeld stuurbare) parameters. Toch zal men in de systeem dynamica zoveel mogelijk de parameters in functie van elkaar uitdrukken door gebruik te maken van constanten, functies, tabellen van een output (van een externe bron die niet door het systeem beïnvloed wordt) die als input in functie van de tijd gebruikt wordt, enz...
Dit toont duidelijk de kracht van deze benadering: de kwalitatieve waardering van de dynamiek kan gemodelleerd worden, zelfs als de niveaus niet als kwantiteiten kunnen uitgedrukt worden. Maar omdat mensen niet gewoon zijn om te denken in termen van verandering moeten de schema's zorgvuldig uitgelegd worden. Een veel voorkomende gewoonte die inzicht blokkeert is te denken aan feedback in termen van "goed" (of "positief") en "slecht" (of "negatief"). Systeem dynamica modelleert op de eerste plaats spontaan gedrag en slechts weinig aspecten van spontaan gedrag zijn stuurbaar. Trouwens: de meest betrouwbare (anticipeerbare) processen zijn de processen die niet stuurbaar zijn (die door de betrokken agentia niet beïnvloed kunnen worden). Feedback is onvermijdelijk (er zal ook altijd iets gebeuren, dat niet bedoeld was), dus feedback kan niet worden geclassificeerd als "goed" of "slecht". Men zou als een schema als “goed” kunnen classificeren wanneer men in staat is om meer lussen te sluiten, en "slecht" als dit niet lukt. Maar zelfs die laatste classificatie loopt mank, omdat zal blijken dat het onmogelijk is om te anticiperen op alle aspecten die in actie relevant zouden blijken te zijn.
In de meeste literatuur in de systeem dynamica heet een positieve feedback "versterkend" en een negatieve feedback heet "evenwicht zoekend".
De resulterende diagrammen zullen grotere lussen laten zien met deelprocessen die ofwel een “positief teken” hebben, ofwel een “negatief teken”. Soms worden ook pijlen getekend die een causale interpretatie ondersteunen. Eigenlijk zijn ze overbodig, zoals het ook overbodig is om met sommige relaties of buffers het diagram nog indrukwekkender te maken.
In een eerste, klassiek geworden diagram, gebruiken we een volle lijn voor een transformatie en processnelheid met een positieve feedback relatie en een onderbroken lijn voor een transformatie en processnelheid met een negatieve feedback relatie.
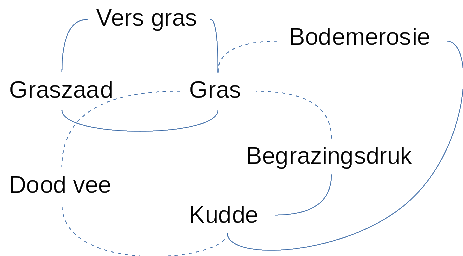
Een groter proces is dan globaal ofwel een positieve of negatieve feedback en dit geldt dan ook voor gesloten lussen. We kunnen dat als volgt vaststellen: een even aantal negatieve relaties (of geen negatieve relaties) resulteert in een positieve feedback een oneven aantal negatieve relaties resulteert in een negatieve feedback. Soms is het weinig intuïtief om in het algemene beeld een positieve feedback te herkennen in twee negatieve relaties, maar gedetailleerd onderzoek zal dit altijd duidelijk maken, wat we met het voorbeeld kunnen illustreren.
In dit systeem kunnen we onder andere de volgende lussen onderscheiden:
Meer "Gras" leidt tot meer "Graszaad", wat leidt tot meer "Vers gras", en steeds meer "Gras" ... OF ... Minder "Gras" leidt tot minder "Graszaad", wat leidt tot minder "Vers gras", dat leidt tot minder "Gras". Omdat meer "Gras" leidt tot meer "Gras" en minder "Gras" leidt tot minder "Gras", is dit een positieve terugkoppeling (versterkende lus). Dit is een lus zonder negatieve relaties. Meer "Gras" leidt tot meer "Gras", minder "Gras" leidt tot minder "Gras".
Meer "Gras" leidt tot minder "Bodemerosie" wat leidt tot meer "Vers gras" wat leidt tot meer "Gras" ... of ... Minder "Gras" leidt tot meer "Bodemerosie" wat leidt tot minder "Vers gras" wat weer leidt tot minder "Gras". Dit is een positieve terugkoppeling (versterkende lus). Dit is een lus met een even aantal negatieve relaties. Meer "Gras" leidt tot meer "Gras", minder "Gras" leidt tot minder "Gras".
Meer "Gras" leidt tot minder "Dood vee", wat leidt tot een grotere "Kudde", wat leidt tot een hogere "Begrazingsdruk" wat leidt tot minder "Gras" ... OF ... Minder "Gras" leidt tot meer "Dood vee" wat leidt tot een kleinere "Kudde" wat leidt tot een lagere "Begrazingsdruk" wat leidt tot meer "Gras". Dit is een negatieve feedback lus (evenwicht zoekende lus). Dit is een lus met een oneven aantal negatieve relaties. Meer "Gras" leidt tot minder "Gras", minder "Gras" leidt tot meer "Gras".
Een grotere "Kudde" leidt tot meer "Bodemerosie", wat leidt tot minder "Gras", wat leidt tot meer "Dood vee", wat leidt tot een kleinere "Kudde", ... of ... een kleinere "Kudde" leidt tot minder "Bodemerosie", wat leidt tot meer "Gras", wat leidt tot minder "Dood vee", wat leidt tot een grotere "Kudde". Dit is een lus met een oneven aantal negatieve relaties, dus een negatieve feedback lus. Een grotere "Kudde" leidt tot een kleinere "Kudde", een kleinere "Kudde" leidt tot een grotere "Kudde".
Verhogen van iets kan leiden tot een verdubbeling van dat iets en dat neemt een tijd in beslag: de verdubbelingstijd. Verlagen van iets kan leiden tot een halvering van dat iets en dat neemt een tijd in beslag: de halveringstijd. Verdubbelen of halveren is zeer relevant maar niet evident omdat we zeer complexe eenheden tellen (we zullen bijvoorbeeld niet onmiddellijk “dood vee” tellen en een half-dode koe bestaat niet).
Het is duidelijk dat veel beïnvloedende parameters niet vernoemd werden. Bijvoorbeeld "Bodemerosie" en "Kudde" zijn positief gerelateerd, maar andere relaties die van invloed zijn voor beide zijn niet onderscheiden, zoals bijvoorbeeld de klimatologische omstandigheden, de tijd die het duurt om van graszaad gras te maken, een migratie van de kudde over een gegeven oppervlakte creëert meer impact op de bodem, enz …. Sommige van die nieuwe parameters zouden als regelbare aspecten kunnen gebruikt worden. Zoals gewoonlijk wordt het model beperkt door onze beperkte creativiteit. Een model maakt altijd een selectie van relevante aspecten. Een systemisch model probeert altijd zoveel mogelijk lussen te sluiten omdat we geïnteresseerd zijn in het modelleren van spontaan gedrag. Aspecten die geen deel uitmaken van een lus worden beschouwd als exogeen aan het systeem (bijvoorbeeld in- en output die elkaar niet beïnvloeden). Nieuwe beïnvloedende aspecten dienen minimaal op nominaal niveau gedefinieerd te worden en zo spoedig mogelijk moet een methode worden ontworpen om ze te definiëren op een ordinaal niveau. Als de meetmethode niet kan worden verduidelijkt, kan het schema niet worden uitgelegd.
Om een coherent model te maken moet er voor gezorgd worden dat alle dimensies van de metingen compatibel zijn. Bijvoorbeeld, een knooppunt in het schema dat de hoeveelheid gras relateert met de kudde is "Begrazingsdruk" genoemd. Dit betekent de hoeveelheid gras gegeten per oppervlakte, het directe gevolg is dat de relevantie van het gehele diagram betrekking heeft op een ongewijzigde oppervlak beschikbaar voor gras en het vee. Het zou dus minder verwarrend zijn als we de buffer “Kudde” "Oppervlak dichtheid van de kudde" zouden noemen.
Ook al is het zinvol om een knooppunt "Begrazingsdruk" in te voeren, is het een processnelheid en niet een niveau. Grazen is een werkwoord en dus een veranderende actie. Dit wordt gemakkelijk gezien door het stopzetten van de dynamiek: als er niets verandert, is er geen "Begrazingsdruk", maar er is nog steeds een "Oppervlaktedichtheid van de kudde". De "Begrazingsdruk" kan ook veranderen, niet enkel door de grootte van de kudde maar door de honger van individuele dieren (de druk die elk dier voelt om te grazen). Maar is dat een relevant onderscheid, met andere woorden: is de begrazing stuurbaar? Elk diagram is maar nuttig als we er mee een dynamisch verhaal kunnen modelleren.
Soms worden processnelheden aangegeven met een pijl om een onderscheid te maken tussen de in- en uitstroom van een gekozen niveau (waarmee men vaag iets van causaliteit wil modelleren). Dit is zeker zinvol voor buffers die zich gedragen als een bad: het bad kan slechts geledigd worden als het voordien al water bevatte en een leeg bad kan altijd gevuld worden. Maar laten we nu de gesloten lus A↔B↔C↔A veronderstellen. Wanneer men deze gesloten lus een causaal diagram noemt, dan komt de verwijzing naar causaliteit van het gegeven dat de dubbele pijl in deze lus ofwel kan geïnterpreteerd worden als “een noodzakelijke oorzaak voor” ofwel als “een noodzakelijk gevolg van”, maar dat een mengeling van beide interpretaties niet kan (het is bijvoorbeeld zo dat als A een noodzakelijke voorwaarde is voor B, het niet hoeft te zijn dat B een noodzakelijk gevolg zou zijn van A). Indien men de lus dus woordelijk wil interpreteren, dan kan dat ofwel met enkel een rechter pijl, ofwel met enkel een linker pijl. De lus als zodanig overstijgt deze twee interpretaties (anders gezegd: de lus is abstracter). Dit is niet anders dan “de kip of het ei” problematiek: het is niet omdat een kip noodzakelijkerwijze uit een ei komt dat daarom de kip noodzakelijkerwijze een ei moet leggen. Maar als we zowel kippen als kippeneieren waarnemen dan zijn ze in een gesloten lus met elkaar gerelateerd. Een kippenei is een noodzakelijke oorzaak voor een kip en een kip is een noodzakelijke oorzaak voor een kippenei. Ofwel: een kippenei is een noodzakelijk gevolg van een kip en een kip is een noodzakelijk gevolg van een kippenei. En natuurlijk maken we dan abstractie van een hele omgeving die een noodzakelijke oorzaak en een noodzakelijk gevolg zijn voor de aanwezigheid van kippen en (bevruchte) kippeneieren, en maken we abstractie van individuele kippen en individuele kippeneieren (dit ei is misschien niet van deze kip).
Bij het gebruik van de pijlen kan men echter altijd twee vragen stellen: "is dit niveau een noodzakelijke voorwaarde voor het volgende niveau" en, volledig duaal: "is dit niveau een voldoende voorwaarde voor het volgende niveau". Als het antwoord “neen” is (op de eerste vraag of de tweede vraag) dan heeft men in het model zeker factoren over het hoofd gezien en dan kan een argumentatie starten of we deze factoren als relevant willen erkennen. De relevantie in de systeem dynamica is de stuurbaarheid van een proces.
Causale diagrammen blijken zeer effectief te zijn om de aspecten van de dynamiek van systemen aan alle betrokkenen duidelijk te maken. Ze gelden ook voor de interacties die niet kwantitatief meetbaar zijn. Maar het gedrag in de tijd kan alleen worden gesimuleerd met (gekwantificeerde) stock-flow simulaties omdat enkel een interactie van gekwantificeerde processnelheden dit toelaat. De stock-flow diagrammen zijn kwantitatieve modellen en hebben het enorme voordeel dat ze de dynamiek van toenemende en afnemende aspecten in de tijd kunnen laten zien. Ze maken het ook mogelijk om vertragingen te modelleren doordat buffers kunnen gekwantificeerd worden die daardoor discontinu van invloed zullen zijn (bijvoorbeeld: slechts als de buffer volledig gevuld is wordt de volgende actie ingezet). Ze dwingen degene die modelleert na te denken over de meeteenheden van buffers en tijd (wat is een processtap?) en de coherentie van de gebruikte eenheden en functies. Maar ze hebben zeker ook het nadeel dat de meest interessante aspecten gewoonlijk op maximaal ordinaal niveau gekend zijn, of dat in een eerste benadering van een model enkel nominale begrippen kunnen gebruikt worden die niet op een ordinale schaal kunnen gerangschikt worden. Bovendien wordt teveel verwacht van een simulatie. Een simulatie geeft een anticipatie, maar niet een voorspelling van de toekomst. Hoe dan ook zijn deze modellen de beste die we hebben om inzicht te krijgen in dynamische systemen en om de verschillende acties en (beleids)maatregelen te simuleren die de dynamiek zouden kunnen beïnvloeden.
Wat we moeten modelleren is de intensiteit van een eenheid die “gevuld” wordt (positieve of negatieve feedback in de positieve zin) of die “geledigd” wordt (positieve of negatieve feedback in de negatieve zin) en dus de meest algemene patronen van interactie van exponentieel gedrag, inclusief de mogelijkheid dat ook eigenwaarden afhankelijk zijn van de intensiteit van eenheden. De verandering van een eigenwaarde wordt gemakkelijker geïnterpreteerd als de verandering van een verdubbelingstijd of halfwaardetijd. Dit is het inzicht dat het mogelijk maakt de stock-flow diagrammen te begrijpen. In deze diagrammen veronderstelt men altijd een bron (source) en een put (drain) die het causaal diagram voeden of ontlasten. Deze worden verder niet gespecificeerd en in het diagram worden ze soms door een wolkje voorgesteld. Zij kunnen nooit deel uitmaken van een gesloten lus aangezien noch bron noch put kan veranderen van intensiteit, ze leggen enkel een causale relatie vast: de zin van de veranderingen is van een van de bronnen naar een van de putten. Ze zijn de motors van de simulatie en om dat te benadrukken wordt een pijl gebruikt en een symbool dat verwijst naar een kraan op een leiding. De interpretatie aan de bron-zijde is dat dit de instroom regelt, de interpretatie aan de put-zijde is dat dit de uitstroom regelt. Die instroom node en uitstroom node worden dan deel van een gesloten lus en die lus is ofwel een positieve feedback lus ofwel een negatieve feedback lus en dat hangt natuurlijk af van wat men wil modelleren.
Een gevolg van de kwantitatieve ambitie van het model is ook dat alle doelen en anti-doelen expliciet moeten gemodelleerd worden. Een doel wil men bereiken en dus het verschil met het doel moet verkleind worden. Een anti-doel wil men vermijden en dus het verschil met het anti-doel moet vergroot worden. Men wil dat soms ook zo snel mogelijk doen, dus het verschil op twee verschillende stappen van het verschil met het doel moet ook gemodelleerd worden en dit is dus de halveringstijd (hoe groter de eigenwaarde, hoe kleiner de halveringstijd) voor een negatieve feedback of de verdubbelingstijd voor een positieve feedback.
Een doel is natuurlijk ook aan verandering onderhevig en daarom spreken we liever van een uitdaging voor het voortbestaan van de entiteit onder focus. De uitdaging kan invariantie zijn, maar de uitdaging kan ook verandering zijn. Het model dat van het systeem moet gebouwd worden komt dus neer op een spanning tussen invariantie en verandering. Een buffer moet invariant gehouden worden (en wordt dan gestuurd met behulp van negatieve feedback) en een andere buffer mag niet invariant gehouden worden (en wordt dan gestuurd met behulp van positieve feedback).
In het volgende “causal loop” diagram dat een zeer algemeen voorkomende uitdaging modelleert voor gelijk welke menselijke onderneming (Sterman MIT) wordt de overgang duidelijk naar “stock-flow” diagrammen. In “stock-flow” diagrammen kan men expliciet hoeveelheden linken aan snelheden en zal men een paar intensiteiten kiezen waarvan men toename en afname afzonderlijk zal verbinden met andere intensiteiten. Die intensiteiten zijn stuurbaar door het input proces en het output proces met een andere intensiteit te verbinden. In het onderstaand voorbeeld zijn dit “Uitdaging” en “Vaardigheden”. De input van “Uitdaging” bijvoorbeeld wordt deels stuurbaar door in te spelen op “Machine veroudering, verwaarlozing, nieuw personeel, nieuwe producten, technieken” maar ook op “nieuwe toepassingen, doelen, gedrag”. Men modelleert in dit diagram dus dat “Uitdaging” en “Vaardigheden” stuurbaar zijn, en de andere buffers worden als niet regelbaar verondersteld. Een aantal relaties wordt ook niet gemodelleerd, bijvoorbeeld de positieve relatie tussen “Technische, organisatorische complexiteit” en “Vaardigheden”, en daarenboven suggereert de naamgeving dat “Uitdaging” als een probleem beschouwd wordt en de performantie negatief beïnvloedt. Dit kan ook afgeleid worden door het gebruik van het begrip “halfwaarde tijd”: men wil de uitdaging verminderen en dus speelt men in op de output snelheid van “Uitdaging” die men probeert te vergroten. Maar daardoor beïnvloedt men ongewild ook de input snelheid van “Uitdaging”.
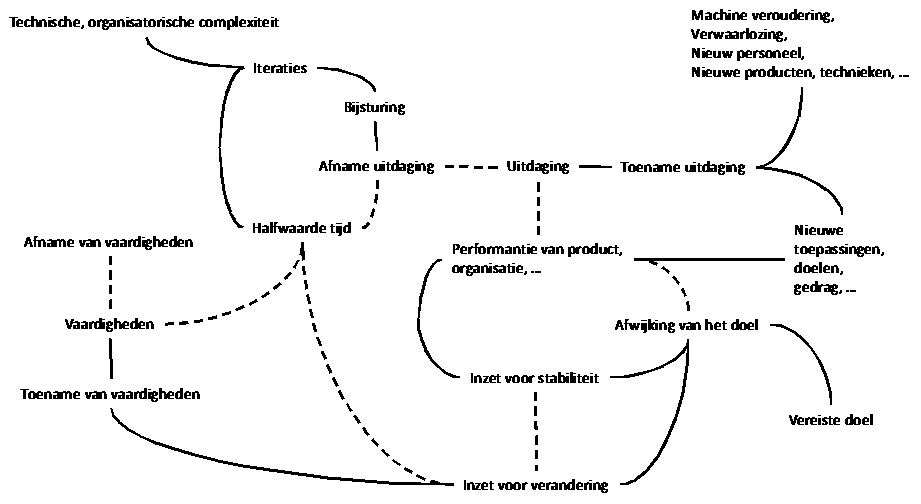
Merk
op dat “Uitdaging” op elk moment een bepaalde intensiteit heeft.
Stop de tijd en “Uitdaging” heeft een intensiteit (zoals ook alle
andere nodes). Stop de tijd en “Afname uitdaging” en “Toename
uitdaging” hebben geen intensiteit. De intensiteit van
“Uitdaging” is de “balans” van toename en afname en dus is de
volle lijn die “Uitdaging” met “Toename uitdaging” verbindt
niet absoluut, evenmin als de gestippelde lijn die “Uitdaging”
met “Afname uitdaging” verbindt. Hetzelfde kunnen we doen voor de
node “Vaardigheden”. Dat zijn de enige twee nodes in het schema
die een gemodelleerde processnelheid hebben. Elk model dat een beeld
wil geven dat geen rekening houdt met tijd heeft zijn beperkingen en
een inzicht in de tijd moet gesimuleerd worden.
De fundamentele reden voor de zorgvuldige behandeling van zowel “causale diagrammen” als van “stock-flow diagrammen” is dat degene die modelleert gewoonlijk geen duidelijk onderscheid modelleert tussen informatie en energie/materie. Alleen energie/materie zijn rivaliserende kwantiteiten die in spontane processen gedissipeerd worden in ruimte en tijd. Dit is niet het geval voor informatie. Men kan informatie op andere plaatsen en andere tijden accumuleren zonder verandering (vermeerdering of vermindering) van het informatieniveau aan de bron. Informatie wordt gemeten als het verschil van (informatie)entropie voor en na de informatie overdracht. Dit is dus een verandering in de relevante toestandsruimte. Dit is heel verschillend van de energetische entropie die in een vaste toestandsruimte gedefinieerd is. Een toestandsruimte zijn alle conjuncties van onderscheidingen en elke interactie kan steeds in verschillende onderscheidingen universa gemodelleerd worden.
Sommige fenomenen kunnen niet deterministisch gemodelleerd worden. Analytische modellen zijn zelfs niet relevant voor de modellen in de cybernetica omdat de analytische modellen impliciet deterministisch zijn: verleden, heden en toekomstig gedrag worden perfect voorspeld door die modellen en hun waarnemingsresolutie. De cybernetica “moet zijn toevlucht nemen” tot numerieke methoden, zogezegd om analytische modellen te simuleren met “gewogen” stappen (bijvoorbeeld de Euler methode, Runge-Kutta en andere lineaire multi-stap methodes). De meest toepasselijke schaal (en dus eenheid) is dan gevonden wanneer er geen verschil meer is met de resolutie van de waarneming en de keuze van de eenheden die als belangrijk erkend worden. Die bepaalde schaal definieert dan impliciet de onderzoekseenheid die gemodelleerd wordt (dus zonder dat die eenheid expliciet vermeld wordt). Dat geldt dan voor spontaan gedrag, maar niet alle gedrag is spontaan en een beslissing om een bepaalde richting in te slaan op een bepaald moment genereert discontinuïteiten.
Wanneer men dus op een fundamenteel niveau de veronderstellingen van de systeem dynamica blootlegt, dan kan men ook begrijpen waarom er zoveel aandacht gaat naar “gevoeligheidsanalyse” waarbij men zich noodgedwongen afvraagt wat “de juiste tijdstap” moet zijn en "de juiste integratie-methode". Het is a priori immers niet mogelijk de juiste tijdstap te kiezen aangezien de systeem dynamica de processnelheid van de overgang van toestand naar toestand modelleert. Aangezien de toestanden niet a priori gekend zijn, is ook de tijdstap niet a priori gekend waarbij de ene naar de andere toestand overgaat. Het is a priori evenmin bekend welke “numerieke benadering” moet gebruikt worden (Euler, Rung-Kutta en andere) om de “correcte” simulatie te geven, opnieuw aangezien de aard van de functie die wordt benaderd niet a priori bekend is en zelfs niet bekend kan zijn. Er worden dan ook een aantal heuristieken toegepast die afgeleid zijn van de modellering van continu veranderende modellen, modellen van processen in de werkelijkheid die met deterministische precisie met behulp van continue functies kunnen gemodelleerd worden.
We hebben daarom een nieuwe “speciale som” moeten introduceren (de cumulatie) om het verschil te kunnen maken tussen eenheid en intensiteit die relevant zijn in de cybernetica en de systeemdynamica.
Een twijfelachtige procedure die zelden in vraag gesteld wordt is om exogene gegevens te importeren in het model (bijvoorbeeld historisch verantwoorde trends, parameters enz …). Dikwijls wordt impliciet aangenomen dat ze geen onderlinge relatie met elkaar of met de buffers en de processnelheden hebben die expliciet opgenomen zijn in het model. Dus men gaat ervan uit dat deze gegevens elkaar niet beïnvloeden en niet beïnvloed worden door de gebeurtenissen die worden gesimuleerd in het model. Bijvoorbeeld is er bij een S-patroon of U-patroon een quasi lineair verband in een bepaald gebied vast te stellen. Stel nu dat dit in het verleden zou waargenomen zijn, dan is het helemaal niet duidelijk met welke vier parameters dat patroon moet gemodelleerd worden en men zou voor de eenvoud de gegevens als lineair kunnen beschouwen en volledig de omslag punten (“tipping points”) kunnen missen.
Zelfs wanneer het model verfijnd is en meer buffers en snelheden onderscheiden en gewaardeerd worden en dus een groter onderscheidingen universum gebruikt wordt, is het nog steeds een model, een vereenvoudigde anticipatie van wat in werkelijkheid zou kunnen gebeuren. Dit is de reden waarom men in het systeem dynamiek benadrukt dat men “zo spoedig mogelijk” een “reality check” moet doen met het model. Men kan zich afvragen wat dit betekent voor uitgebreide modellen zoals het World3 model.
De meest succesvolle modellen uit de systeem dynamica modelleren de toename en afname van de intensiteit van fysiek gescheiden subsystemen (onderdelen van een constructie) die materie en energie pakketjes uitwisselen. Van zodra daarvan afgeweken wordt en aspecten een rol spelen die veranderende informatiecontexten modelleren sputteren de modellen. De fundamentele reden hiervoor is dat men dan onderscheidingen zou moeten modelleren en de toename en afname (divergentie en convergentie) in onderscheidingen universa. Overvloed (geen schaarste) is een bepalende eigenschap van informatie en creativiteit. Informatie kan "kennis" of "know-how" genoemd worden en verhoogt zo de “toegang” tot nieuwe middelen, wat betekent dat dank zij creativiteit andere niet concurrerende middelen kunnen gevonden worden waarmee schaarste voorkomen kan worden. Bovendien kan creativiteit worden gericht op de organisatie van een synergie van acties om middelen beschikbaar te stellen (een coördinatie van acties). Een poging om daaraan tegemoet te komen wordt geschetst in F. Heylighen: Mediator Evolution: een algemeen scenario voor de herkomst van dynamische hiërarchieën. Hij besluit dat er een onvermijdelijke hiërarchie ontstaat voor informatie en betekenis: een collectief van agentia beginnen te interageren, waardoor een medium ontstaat, medium dat zichzelf organiseert om de interacties beter te coördineren, wat hij een mediator noemt; de mediator gaat actieve controle uitoefenen over de interactie van agentia, wordt een manager die actief een bepaalde betekenis in de interacties gaat promoten. Hier wordt het begrip “manager” gebruikt zoals in een holarchie. Als deze hiërarchieën gematerialiseerd worden in een hiërarchie van betekenisvolle sporen, dan zal de toenemende synergie niet verloren gaan en nog hogere coördinatieniveaus mogelijk maken.
Uit de systeem dynamica zijn inzichten gegroeid die nuttig zijn wanneer men aangrijpingspunten zoekt om de werkelijkheid te veranderen en men de mogelijkheid om te veranderen wil open houden. Sommige veranderingen zullen simultaan doorgaan en dus is er een hiërarchie in de veranderingen die men introduceert (wat ook weer het bestaan van een hiërarchie verklaart). Het voorbeeld hiervan dat volgt is geïnspireerd door “Places to intervene in a system (in increasing order of effectiveness)” (Donella Meadows 1999). Zij onderscheidde als eerste een hiërarchie in de interventies die men kan uitvoeren in een systeem en gaf een lijst van interventies in volgorde van toenemende effectiviteit (wat betekent dat op het meest gespecificeerde niveau de minste veranderingen mogelijk zijn, dus de meeste veranderingen onmogelijk zijn). Een verandering in het hiërarchisch niveau h (met h van 1 tot 12) zal simultaan het hiërarchisch niveau h+i veranderen (met i van 1 tot 11), anderzijds zal een verandering in het niveau h+i onvermijdelijk een verandering in het niveau h nodig maken, wat de hiërarchie demonstreert.
De tabel toont in de eerste kolom 12 niveaus. Het niveau nummer 12 is het minst effectieve en meest gespecificeerde, het niveau nummer 1 is het meest effectieve en het minst gespecificeerde. In de tweede kolom wordt de focus vermeld van wat men verandert. De derde kolom geeft wat achtergrond en de logica van de hiërarchie. Voorbeelden zijn te vinden in de tekst van Meadows.
12 |
Hoeveelheden (aantallen) veranderen |
Er wordt geïmpliceerd dat de in- en uit-stroom van buffers rivaliserende entiteiten veronderstellen. Dit betekent dat een entiteit die zich in buffer A bevindt zich niet in buffer B kan bevinden, dus
De impliciete veronderstelling is dus dat XOR (exclusieve disjunctie) niet verschillend is van OR (inclusieve disjunctie) voor de pakketjes, en dit komt overeen met het klassieke wereldbeeld (in tegenstelling met bijvoorbeeld het wereldbeeld van de kwantummechanica). Eens alle relevante entiteiten en hun onderlinge relaties vastliggen en dus een volledig dynamisch model beschikbaar is, kan men nog enkel variëren op de veranderende aantallen van de relevante entiteiten. Men kan dan de relaties tussen entiteiten vergeten (aangezien ze toch niet te veranderen zijn) en enkel sturen op intensiteiten. Dit is wat men doet met de modellen die beschikbaar zijn in de “system dynamics”. Dit toont de kracht maar ook de beperking van “system dynamics”. Men ontwikkelt een performant model dat men dan bevraagt door parameters aan te passen die de input en output regelen. Dit kan de ogen openen omdat hiermee tweede orde effecten duidelijk kunnen gemaakt worden (“rebounds” enz...) die helemaal niet intuïtief konden vermoed worden. Dit is al complex genoeg, maar als hefboom voor verandering is dit de minst effectieve! Hier vind je alle methodieken van kwaliteitszorg, supply chain management, LCA, LCE, materiaalstromen, emissiestromen, C2C, duurzaamheid, circulariteit, enz... |
11 |
Grootte van buffers vergeleken met de in- en uit-stroom veranderen |
Een buffer heeft minstens één pakketje, een minimum. De toename of afname van de intensiteit van de buffer modelleert de relatie tussen instroom en uitstroom. Minimum en maximum van de buffers moeten niet a priori vastliggend verondersteld te worden. We kennen een bron buffer waarvan we merken dat we die niet kunnen uitputten, we kennen een put buffer waarvan we merken dat we die niet kunnen opvullen. We kunnen de grootte van een buffer dus proberen te veranderen om ze meer het karakter van een bron of een put te geven. Organisaties zullen bijvoorbeeld groter worden wanneer het nodig is om te overleven ondanks lokale tegenslagen (wanneer lokale processen niet meer kunnen doorgaan, toch blijft dan de globale stroom bestaan). Wanneer dieren groter worden in de evolutie zullen ze meer warmte kunnen bufferen in hun volume dan wanneer ze kleiner zouden worden, ze kunnen grotere temperatuurschokken aan. |
10 |
De relatie tussen buffers met behulp van de in- en uit-stroom veranderen |
Meerdere entiteiten zijn met elkaar gerelateerd en elk doorloopt een baan in de eigen toestandsruimte. Maar zij bevinden zich ook in een gemeenschappelijke toestandsruimte. De impliciete veronderstelling hier is dat de gemeenschappelijke toestandsruimte gemodelleerd wordt door het cartesiaans product van de individuele toestandsruimten (enkel mogelijk als XOR (exclusieve disjunctie) niet verschillend is van OR (inclusieve disjunctie) voor de pakketjes). Indien de totale som van de pakketjes niet verandert, is er op dit moment een verdeling van toestanden over de entiteiten die sterk bepaald wordt door de aanwezigheid en de soort verbindingen waarover pakketjes uitgewisseld worden. Het veranderen van de relaties waarlangs pakketjes verdeeld worden is dus een krachtig aangrijpingspunt voor verandering. We zouden tussen bestaande buffers met bestaande relaties nieuwe relaties kunnen ontwerpen zonder meer of minder buffers te ontwerpen. Hier op zich is al een enorme uitdaging aan verbonden voor duurzaamheid, denk aan een meer rechtvaardige verdeling van rijkdom, kansen, enz... en we zijn nog maar op niveau 10! |
9 |
De duur van reactie (de grootte van de vertraging bijvoorbeeld) vergeleken met de snelheid van verandering veranderen |
Waar bevindt zich elke entiteit op dit moment in de ruimte van verdeling van pakketjes? Is dat waarneembaar en kunnen we daarmee sturen? Dit is een nieuw soort vraag. Voor sommige entiteiten zijn sommige veranderingen gedurende lange tijd niet waarneembaar (fase-overgangen, step-functies, buffering, resolutie, relevantie, ...) of kunnen niet gekozen worden, kunnen enkel maar gebeuren (sommige processen verlopen spontaan en kunnen niet anders verlopen). Hier doet het begrip informatie zijn intrede, concept met niet rivaliserende aspecten. Het is immers niet zo dat als er informatieoverdracht bestaat tussen buffer A en buffer B dat dan de informatie uit buffer A zou verdwijnen. Hiermee wordt de overgang gemaakt van entiteiten naar onderscheidingen. Dit is een moeilijke conceptuele stap. Bij stap 9 veronderstelt men dat sommige relaties door terugkoppeling gemodelleerd kunnen worden die gebaseerd is op meting, waarneming, informatie. Feedback zal een β-proces inschakelen nadat een grens overschreden is in het α-proces die niet voorspeld had kunnen worden, die enkel maar kan gebeuren. De vertraging is een gevolg van buffers... in de transmissie bijvoorbeeld, maar ook als een spontaan proces zijn intrede doet. Er is gevaar voor oscillaties wanneer men met terugkoppeling wil sturen. Zowel te kleine vertraging (overreactie), als te grote vertraging (late reactie) kan leiden tot oscillatie en in de limiet tot chaos. Hier bereikt men de grens van de benadering met pakketjes. Dit is een moeilijke conceptuele stap. De relatie tussen het veronderstellen van pakketjes en de waarneembaarheid ervan veronderstelt een waarnemend agens. Een waarnemend agens wordt altijd beperkt (sensoren, gevoeligheid enz...). Hier wordt de grens bereikt van een mechanistische benadering van duurzaamheid en zullen biologen wijzen op het specifieke van levende agentia. |
8 |
De sterkte van negatieve terugkoppeling vergeleken met het effect dat ze wil teniet doen veranderen |
Een negatieve feedback zal, uitgaande van de toename van de intensiteit van onderscheidingen in het α-proces een afname van de intensiteit van onderscheidingen genereren in het β-proces, of van de afname van de intensiteit van onderscheidingen in het α-proces een toename van de intensiteit van onderscheidingen genereren in het β-proces. Negatieve terugkoppeling is een proces dat noodzakelijk is wanneer dat wat niet gekozen wordt om een doel te bereiken (en dus enkel kan gebeuren) het bereiken van iets anders dan dat doel versnelt. Er zijn gewoonlijk meer mogelijkheden tot “het bereiken van iets anders dan het doel”. We zullen sneller iets kapotmaken dan iets nieuw opbouwen en dat is natuurlijk zeer nuttig als we een bedreiging willen wegnemen en er zijn gewoonlijk meer mogelijkheden om de noodzakelijke voorwaarden voor een ongewild proces weg te nemen. Vraag is natuurlijk wat we als een bedreiging herkennen ten opzichte van een kans tot iets nieuws. Dus de sterkte van de negatieve feedback moet overeenkomen met de sterkte van de bedreiging. |
7 |
De winst uit positieve terugkoppeling aanpassen aan de mogelijkheid om negatieve terugkoppeling te maken |
Een positieve feedback zal, uitgaande van de toename van de intensiteit van onderscheidingen in het α-proces een toename van de intensiteit van onderscheidingen genereren in het β-proces, of van de afname van de intensiteit van onderscheidingen in het α-proces een afname van de intensiteit van onderscheidingen genereren in het β-proces. Positieve terugkoppeling is het proces waarbij dat wat niet gekozen wordt om een doel te bereiken (en dus enkel kan gebeuren) het bereiken van dat doel versnelt. Dit exponentieel proces stopt niet zonder een negatief feedback proces en kan uiteindelijk zichzelf vernietigen wanneer het samenspel van processen ofwel chaotisch ofwel onmogelijk wordt. Er zijn gewoonlijk minder mogelijkheden tot “het bereiken van het doel”, vandaar dat ingrijpen op positieve terugkoppeling effectiever is dan het ingrijpen met meer negatieve terugkoppelingslussen die elk hun eigen ongewenste bijeffecten kunnen hebben. Omdat sommige predatoren zelf geen prooi zijn moeten ze zichzelf reguleren en in die regulering moeten ze natuurlijk toch zelf blijven overleven. |
6 |
De structuur van de informatie”stromen” veranderen |
Welke entiteiten genereren relevante informatie voor wie? Wie bepaalt welke de relevante onderscheidingen zijn? Dit maakt het mogelijk om nieuwe terugkoppelingslussen aanvaard te krijgen bij de sturende agentia zodanig dat ze op een goed geïnformeerde manier zichzelf en hun samenwerking kunnen sturen. Creativiteit doet zijn intrede. Er kan gestuurd worden op nieuwe aspecten op voorwaarde dat ze door de betrokken agentia waarneembaar zijn, waardevol zijn en gerelateerd aan de veranderingen. |
5 |
De regels (structuur) van het systeem veranderen |
Nieuwe entiteiten doen hun intrede (zoals bijvoorbeeld de emissierechten) en veranderen de interacties en dus het systeem. De regels leggen de onderscheidingen vast, de keuzevrijheid die tussen deze verondersteld of toegelaten wordt. Hier worden nieuwe waarden gecreëerd. Regels worden hier voornamelijk bedoeld voor de niet rivaliserende aspecten (immers: de wetten voor materie en energie kunnen niet zomaar gekozen worden) en worden maar effectief als er "maatschappelijke consensus" is of als ze door “een macht” opgelegd worden. Een entiteit wordt gerealiseerd in een toestandsruimte en heeft een toestand als een intensiteit die in de loop van de tijd verandert van minder waarschijnlijk (meer specifiek) naar waarschijnlijker (minder specifiek). De waarschijnlijkheid neemt toe in de loop van de tijd en dus neemt de specificiteit af. De plaats van de entiteit in de toestandsruimte meten we door zijn entropie. Er is een groot verschil tussen de informatie entropie (niet rivaliserend) en de energetische entropie (rivaliserend). Waar bevindt zich de entiteit op dit moment in de toestandsruimte? Een entiteit die zich op een minder specifieke plaats bevindt is niet zo specifiek dat hij veranderd wordt door de verandering in het spontaan proces. Dit gelijkt op een buffer, maar dan een buffer van mogelijkheden (informatie) in plaats van rivaliserende aspecten en geeft aanleiding tot veel contra-intuïtieve effecten (zoals bij de kwantummechanica). |
4 |
Alle aspecten van het systeem veranderen |
Creativiteit kan de regels veranderen. Creativiteit kan het systeem veranderen, verandering wordt gestuurd door zelf te veranderen, door zelf creatief te zijn maar is niet voldoende voor het veranderen van een totaal-systeem. Creativiteit is mogelijk voor alle mogelijke aspecten, techniek, cultuur, gedrag… Creativiteit geeft de mogelijkheid tot zelforganisatie en het ontwerpen van nieuwe systemen van zelforganiserende deelsystemen. Agentia moeten zichzelf kunnen organiseren omdat ze allemaal een verschillend onderscheidingen universum opspannen. |
3 |
De doelen van het systeem veranderen |
De doelen leggen de onderscheidingen vast, de keuzevrijheid die tussen deze verondersteld of toegelaten worden zonder dat men een van de mogelijkheden moet kiezen (een doel is op verschillende manieren te bereiken). Doelen zijn dus heel abstracte constructies, zeer uitgebreide disjuncties. De meest uitgebreide disjuncties zijn te vinden in de meest uitgebreide onderscheidingen universa. Deeldoelen van systemen zijn soms enkel controle, voorspelbaarheid, het vermijden van verandering, ... zodat meer van hetzelfde bereikt wordt. Soms kunnen enkel deeldoelen veranderd worden. We kunnen proberen om een globaal doel van het leven op de hele aardbol te formuleren als de zo snel mogelijke dissipatie van energie tussen bron en put. Het leven is steeds meer in staat om de uitbundig invallende energie van de zon zo te organiseren dat die energie nog sneller kan dissiperen. Globale systeemdoelen zijn dan overleving, weerbaarheid, diversificatie om een openheid mogelijk te maken voor de mogelijke relaties van simultaneïteit en synergie. Hierin kadert het debat van (bio)diversiteit. |
2 |
Het wereldbeeld dat al de voorgaande genereert veranderen |
Sommige doelen zullen elkaar uitsluiten en dus een waarde krijgen als ze gerealiseerd worden, die waarde kan in vraag gesteld worden zodanig dat men andere doelen kan nastreven. Het onderscheidingen universum kan veranderd worden. |
1 |
De uitsluitende keuze voor één wereldbeeld transcenderen |
Sommige doelen zullen elkaar uitsluiten en dus een waarde krijgen als ze gerealiseerd worden, maar er is een standpunt mogelijk waarbij die doelen als mogelijk en wenselijk gewaardeerd worden zonder ze te waarderen in een realisatie en ze als “indien…, dan…” te blijven beschouwen. De onvermijdelijke realisatie van iets wordt dan als contingent (niet noodzakelijk) beschouwd. Ervaren en ook simultaan iets anders laten gebeuren is onvermijdelijk. |