(ni+nj)/ni=k: positieve feedback
We veronderstellen positieve gehele getallen van één rij: n0, n1, n2, … die sporen zijn van metingen met toestanden T0, T1, .… Hiermee hebben nieuwe getallen als intervallen gemaakt met het patroon vij=(ni-nj)/(ni+nj).
We veronderstellen nu dat er maar één schaalfactor, één verhouding is die een waarde vij=(ni-nj)/(ni+nj) vastlegt voor elke i en j die elkaar opvolgen, noem deze k, verschillend van 1. Uit (ni-nj)/(ni+nj)=k volgt dat (ni-nj)=k(ni+nj) en dus ni(1-k)=nj(1+k) of (1-k)/(1+k)=nj/ni en we herkennen dat deze verhouding de verhouding is van negatieve feedback en positieve feedback bij elke stap van overgang van een toestand naar een andere met k de eigenwaarde van het proces.
Als ni gelijk is aan nj voor elke keuze (bij het bereiken van evenwicht dus) dan moet gelden dat (1-k)/(1+k)=1. Hieruit volgt dat k enkel gelijk kan zijn aan nul en dus geen eenheid kan modelleren. We moeten dus k verschillend van nul veronderstellen en uit (ni-nj)/(ni+nj)=k volgt dat 0<k<1 als we enkel positieve getallen gebruiken (zoals de getallen die we vinden bij elke meting van waaruit een verschil kan berekend worden). De getallen die gegenereerd worden zijn geordend door het cumulatie proces dat op stap s een intensiteit (1-k)s genereert als negatieve feedback en een intensiteit (1+k)s genereert als positieve feedback en dus een verhouding ((1-k)/(1+k))s die simultaneïteit uitdrukt. Verhoudingen zijn onvermijdelijk begrensd. De stap s is niet meer en niet minder dan de schaal waarmee we de exponent van een cumulatie gn kunnen kiezen.
We geven nu een paar voorbeelden met verschillende k. Gemeenschappelijk aan deze voorbeelden is dat er voor elk proces een andere eenheid geldt die de uitdrukking is van een mogelijke transformatie van dezelfde reeks getallen. We laten de processen starten bij n0=1 en we volgen het proces tot n30.
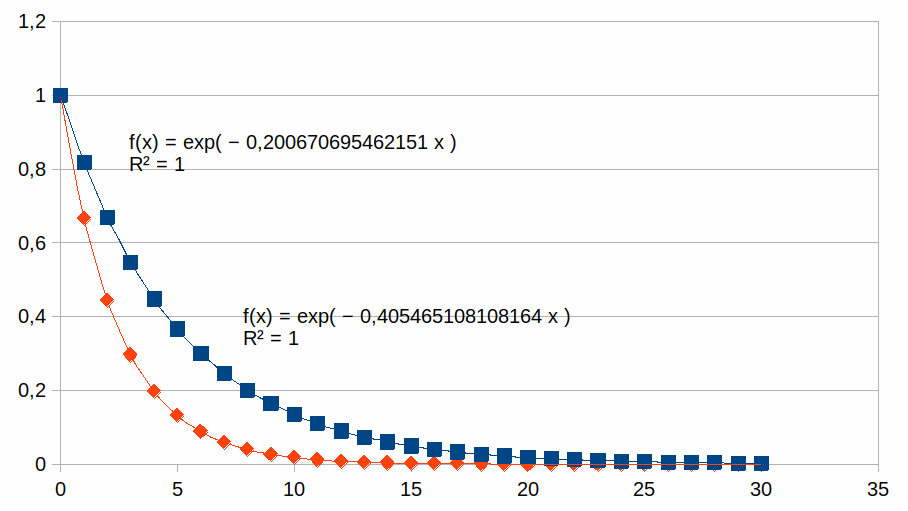
We drukken de volgende stap uit in functie van de vorige stap. Dus (ni-nj)/ni=k schrijven we als (ni-nj)=kni of ni(1-k)=nj. Dus nj=ni-nik. Het rechter lid interpreteren we als ni(1)-nik(1) met eenheid 1.We zien het patroon (x-x0)-k(x-x0)=(x-x0)(1-k) met eenheid (x-x0) dat we herkennen als de eerste stap in een negatieve feedback. We tonen de waarde van ni in de loop van die 30 stappen. De datapunten met vierkant zijn voor een k=0,1. De datapunten met een ruit zijn voor een k=0,2. Het is duidelijk dat evenwicht in het laatste geval in minder stappen benaderd wordt: evenwicht is een situatie waarin het verschil tussen ni en nj zeer klein geworden is en onwaarneembaar kleiner: de waarnemingsresolutie is overschreden.

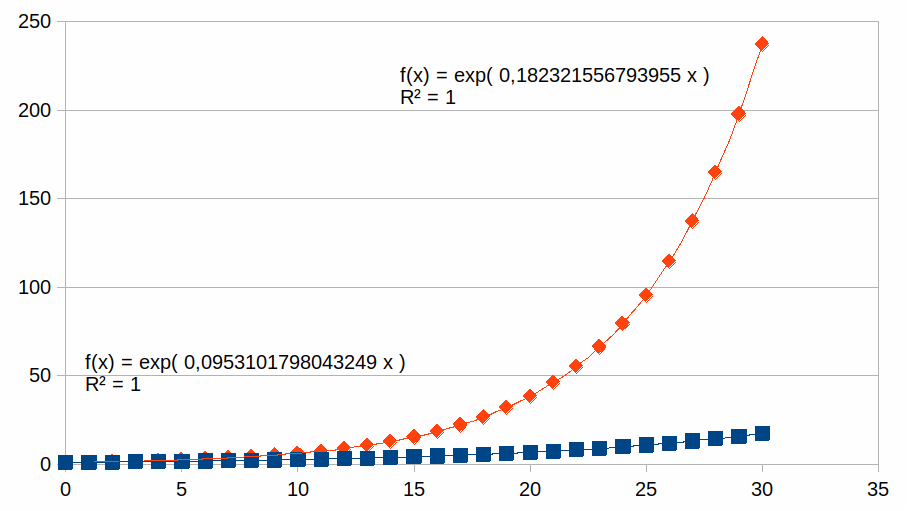
We drukken de volgende stap uit in functie van de vorige stap. Dus (ni+nj)/ni=k schrijven we als (ni+nj)=kni of ni(1+k)=nj. Dus nj=ni+nik. Zoals verwacht modelleert dit positieve feedback. Ook hier kunnen we een waarnemingsresolutie overschrijden, een situatie waarin het verschil tussen ni en nj zeer groot geworden is en onwaarneembaar groter.
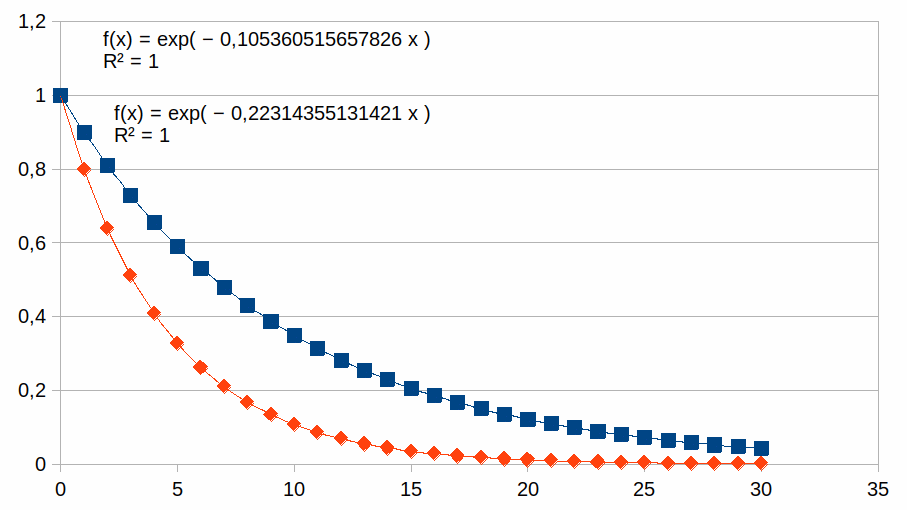
We drukken de volgende stap uit in functie van de vorige stap. Dus (ni-nj)/(ni+nj)=k schrijven we als (ni-nj)=k(ni+nj) of ni(1-k)=nj(1+k). Dus nj=ni(1-k)/(1+k)=ni/(1+k)-nik/(1+k).
Dit is een transformatie van de getallen ni in de eerste veronderstelling, nu is de eenheid in plaats van (1) het getal 1/(1+k). Dit is een voorbeeld waarbij de eenheid een invers priemgetal kan zijn en zo’n eenheid kan op een atoom van een tralie afgebeeld worden. Het patroon van het exponentieel verval in het proces is volledig gelijkaardig als in het eerste voorbeeld: