De fundamentele operatie in het getallendomein is het tellen: de gehele getallen kunnen gebruikt worden om de intensiteit van een eenheid voor te stellen. Tellen is een operatie die discontinu is, er wordt bij het tellen telkens dezelfde eenheid gesommeerd (afgetrokken). De eenheid stellen we voor als het getal 1. De eenheid wordt niet gewijzigd of getransformeerd, enkel de intensiteit wijzigt. Intensiteiten kunnen we verschalen en we kiezen een bepaalde schaal als we ratio meten. Met een verschaling kunnen we uitdrukken dat sommige eenheden invariant zijn voor wat betreft de operatie van het tellen. Alle schalen hebben dan dezelfde kwalitatieve waarde in de zin van “ja”: ze kunnen gebruikt worden zonder de eenheid in vraag te stellen. Als voorbeeld daarvan hebben we de afstand op een landkaart gebruikt: de afstand op de landkaart komt overeen met de afstand die in het landschap zelf kan gemeten worden en verschilt er enkel in waarde van (dat is de kwantitatieve waarde van de schaalfactor die de schaal zelf, de “ja”, kwantificeert). De kwalitatieve waarde is: “ja”, het is een afstand. De veronderstelling die getallen zinvol maakt is de keuze voor één eenheid en één schaal. Dit definieert de intensiteit van één simultaneïteitsinterval. Schaalfactoren zijn dus intensiteiten van een eenheid die staat voor het kleinste interval waarmee een simultaneïteitsinterval kan verdeeld worden in gelijke stukken. Maar we hebben vanuit het onderzoek naar tralies moeten besluiten dat we dan niet alle afstanden in een tralie kunnen voorstellen, we hebben onvermijdelijk een tweede dimensie nodig om een som of verschil van afstanden tussen twee toestanden (dit zijn twee verschillende eenheden) te kunnen uitdrukken. Enkel met een verschil kunnen we dynamiek modelleren. Daarenboven zijn we tot het besluit moeten komen dat daardoor alle afstanden gekromd zijn.

Schalen kunnen we vrij kiezen maar dan moeten we ook rekening houden met de operatie die we willen uitvoeren. Exponentiatie is niet commutatief, het getalproduct wel. Bij het getalproduct kunnen beide getallen de functie innemen van eenheid of van intensiteit. Bij exponentiatie is dat niet zo. In het getallendomein kunnen we enkel getallen hanteren, maar: om met getallen als eenheden tralies op te bouwen hebben we exponentiatie nodig. We tonen nu aan onder welke voorwaarden voor een n in een exponent (n is positief of negatief) we twee (!) schalen kunnen vinden zodanig dat het getal in de exponent zich voordoet als de intensiteit van de eenheid 1 als gewoon getalproduct, dat betekent dus dat gⁿ=ng of dus g^n-1=n, wat duidelijk maakt dat dit voor één (geheel) getal enkel geldt voor n=1. Maar als we g verschillend van 1 nemen, dus van het dubbelgetal type g=(1±k), dan kunnen we n ook als intensiteit beschouwen van g en niet enkel als eenheid. Dat betekent dus dat we kunnen veronderstellen dat we n in (gelijke) stappen kunnen onderverdelen. Op die manier drukken we ook uit dat de priemgetallen de eenheden zijn van deze intensiteiten want enkel voor een priemgetal geldt dat het kan gedeeld worden door één getal verschillend van 1: het priemgetal zelf. Het resultaat van die deling functioneert dus als de eenheid van het priemgetal. Een product van verschillende priemgetallen modelleert dan simultaneïteit: dezelfde intensiteit voor meerdere eenheden is mogelijk. We kunnen dan veronderstellen dat er een zinvolle kleinste eenheid is van die intensiteit, stel 0<1/k<1 met k een positief getal. Dus dat n(1/k)=1 de intensiteit is van die kleinste eenheid (die a priori onbekend is maar verschillend van nul), en daarvan hebben we een onbeperkt aantal ter beschikking, inclusief alle mogelijke producten van priemgetallen die ook als eenheid kunnen gebruikt worden. We berekenen dan het verschil van gⁿ en ng, en we tonen de grafiek f(n)=gⁿ-ng en onderzoeken zijn nulpunten, dat zijn de punten waarbij gⁿ=ng.

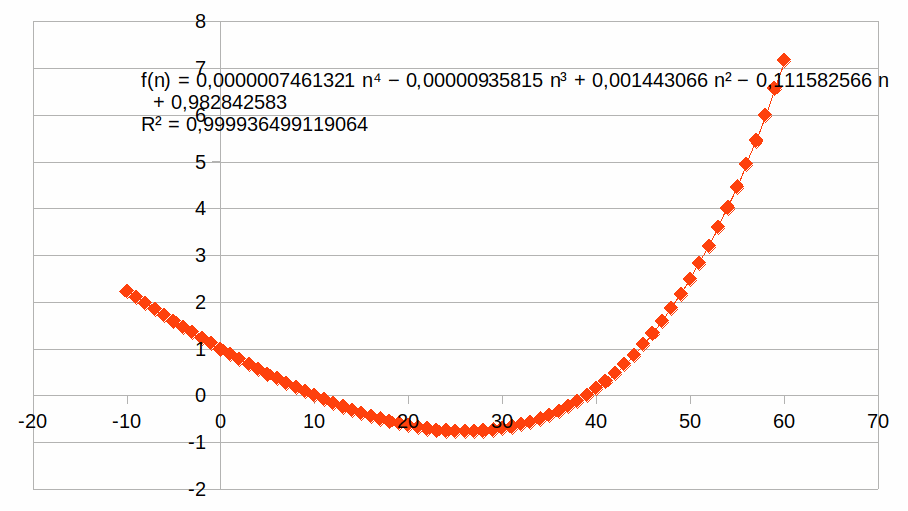
Hieronder de grafiek voor g=(1+0,6) in stappen van 0,1n (de intensiteit n van de zinvolle kleinere eenheid 1/2×1/5, een eenheid waar twee priemgetallen bij betrokken zijn) tussen n=-10 en n=60. Voor n=0 is f(n) natuurlijk 1. De twee stappen waarbij de schaal gelijk is aan 1,6 zijn te vinden voor f(n)=0, namelijk n=10 (dus g^0,1×10-0,1×10g, wat de kleinste stap reflecteert) en een getal n met 38<n<39. In dit tweede geval geldt dan ook (in hybride notatie): g^38<n<39 =(38<n<39)g, en met een resolutie van 15 cijfers is dit n=38,9046357052191. We geven ook de best passende veelterm van graad vier, hoe groter de graad, hoe beter de passing. De passing is te zien aan de determinatiecoëfficiënt R².

De grafiek is afhankelijk van het getal g. We tonen nu ook de grafiek voor g=(1+0,5) in stappen van 0,1n tussen n=-10 en n=60. Voor n=0 is f(n) natuurlijk 1, en de twee stappen waarbij de schaal gelijk is aan 1,5 zijn te vinden voor f(n)=0, namelijk n=10 en 49<n<50.

Dit illustreert een normalisatie die we kunnen doorvoeren door de schaal g aan te passen tussen stap 38<n<39 of 49<n<50 afhankelijk van de eigenwaarde.

Dus elke processtap (dus elke n) vereist een eigen normalisatie om de schaal te kunnen modelleren die de niet commutatieve cumulatie gⁿ (het product van n maal g) gelijkstelt aan de “klassieke cumulatie ng” (de som van n maal g) die wel commutatief is. De twee keuzen voor n waarbij f(n)=0 geven dan, naast het getal 1, ook een tweede mogelijkheid tot normalisatie bij elke stap in een proces waarin we de intensiteit van de eenheid kunnen modelleren als (1±k)ⁿ. Er zijn ontelbaar veel toepassingen van deze inzichten want begrenzing is niet te vermijden.

Typisch zien we nu dat f(n) voor een positieve k twee mogelijke waarden heeft: ofwel positief, ofwel negatief. Kiezen we eigenwaarde k negatief, dan is f(n) monotoon dalend. Bij een eigenwaarde k=1,5937435 is er geen negatieve waarde meer voor de functie en is er maar één nulpunt meer. A fortiori is dit dus ook voor g gelijk aan de constante e van Euler (e=g=2,71828182845904). Dan is de waarde van f(n) altijd positief. Als n groter is dan 1 en bij elke stap groter gekozen wordt, dan is de waarde (1+1/n)ⁿ een steeds betere benadering van het getal e. Door de constante e te gebruiken als grondtal voor exponenten benaderen we dus de werkelijkheid zonder rekening te kunnen (of moeten) houden met schaaleffecten als gevolg van duale (positief versus negatief) relaties. Dit heeft echter andere gevolgen: wanneer we eⁿ schrijven als (1+k)ⁿ, dan is duidelijk dat k=1,71828182845904 en dus is k groter dan 1, en dus zal na één processtap al meer dan een verdubbeling van de gekozen eenheid optreden. Hiermee wordt een fluctuatie rond 1 gemodelleerd die we ook kunnen begrijpen als een trilling die spontaan ontstaat en in fase is met de toenemende stappen, die op een andere schaal (met een andere keuze van k) niet waarneembaar is. Trillingen leiden tot resonantie en dus waarneembaarheid als gevolg van een keuze voor trillingen die in fase zijn en daardoor de amplitude van de trilling in een waarneembaar venster brengen.