Een eigenwaarde k
moet positief zijn om de eigenwaarde als entiteit te kunnen
interpreteren (een entiteit is een eenheid die niet kan
gehalveerd worden). Als k positief is en kleiner dan 1 is ook (1-k)
positief en dus kunnen we deze eigenwaarde ook als entiteit
interpreteren. We zullen dus 0<k<1 veronderstellen. Dat geldt
dus ook voor een veranderende eigenwaarde kn die de rol
kan spelen van een entiteit onder voorwaarde dat 0<kn<1:
kn mag niet negatief zijn, niet gelijk aan nul en evenmin
gelijk aan 1 en zo ook: 0<(1-kn)<1: (1-kn)
mag niet negatief zijn, niet gelijk aan nul en evenmin gelijk aan 1.
De eigenwaarden kn en 1-kn kunnen als
verhouding een begrenzing uitdrukken tussen twee extreme
getallen die nooit bereikt worden. Ze ontstaan wanneer we interactie
van processen niet als som maar als een product modelleren en het
product is niet
gebonden aan een mogelijke ordening van elkaar uitsluitende
stappen in het globale proces. De n van kn verwijst naar
de niveaus die simultaan aanwezig zijn. Een product van getallen
modelleert simultaneïteit in het getallendomein, wat we met de
opbouw van een
tralie met priemgetallen gedemonstreerd hebben. Dit heeft een
belangrijk gevolg voor de interpretatie van de getallen: het getal ki
dat verschilt van het getal ki+1 verwijst naar een
ander niveau in een tralie, dus naar de ordening in een tralie,
een ingebouwde orde. De parameter n verwijst niet naar een
ordening die we verbinden met “tijd”, heeft dus niet als
karakteristiek dat dit een ordening is die niet in een tralie
ingebouwd wordt. Neem dus de entiteit ki, dan is dat een
karakterisering van een niveau in een tralie en dan kan met die
constante ki een cumulatie
gemodelleerd worden (en dat is een tweede soort kwantificering) met
een ordening in de tijd die sporen achterlaat en beschreven wordt met
onderscheidingen die in de tralie niet ingebouwd worden. Dit is iets
anders dan de simultane interactie (het product) van een proces met
eigenwaarde kn en een proces met een “duale”
eigenwaarde (1-kn) die met elkaar gerelateerd zijn door
een eigenwaarde r: we veronderstelden dat dit proces de verandering
tussen 0 en 1 van de eenheid zelf modelleert, eenheid die bij elke
stap verandert en daarom kan geïnterpreteerd worden als een
onderscheiding die telkens ingebouwd wordt, bij elke stap, in
de relevante tralie en daardoor ook de suprema van een deeltralie
verandert. Met deze veronderstellingen hebben we als eerste stap
de
vergelijking ((1-kn)/kn)(1±r)n=1
afgeleid. Karakteristiek is hierbij dat we een buigpunt vinden in de
grafiek halverwege de twee limietwaarden 0 en 1. De eigenwaarde r
kunnen we natuurlijk ook tot een strikte positieve feedback beperken
en die eigenwaarde kan dan natuurlijk terug een eenheid modelleren
met een nieuwe eigenwaarde enz.… Maar dit is niet erg relevant
meer: het patroon van een negatieve r of positieve r is hetzelfde: de
sigmoïde. Het verschil tussen positieve of negatieve feedback is er
een van de zin van de sigmoïde ten opzichte van de ordening van n.
De eigenwaarde kn en de “duale” eigenwaarde (1-kn)
kunnen we ook het getallendomein herkennen en genereert daar de
quaternaliteit
van kettingbreuken.
We zullen nu aantonen dat er door een andere keuze van eenheid in
de vergelijking ((1-kn)/kn)(1±r)n=1,
een nieuw patroon beschikbaar wordt. We hebben dat al aangegeven door
de
schaalfactor K die positief of negatief kon zijn en we zullen dit
nu gedetailleerd modelleren en interpreteren.
Elke eenheid kan een intensiteit krijgen door cumulatie, de
verhouding van die intensiteiten zullen we ook hier zien in de
intensiteit van 1, zoals duidelijk wordt met de vergelijking
((1-kn)/kn)(1±r)n=1. Immers met
intensiteiten K1 en K2 wordt dit
(K1(1-kn)/K2kn)(1±r)n=K1/K2(1).
Dus ook (1±r)n=Rn kunnen we interpreteren als
een schaalfactor die een functie is van n. Er geldt dan voor elke n:
kn=(1-kn)Rn. Dat zijn drie getallen,
kn, (1-kn) en Rn, die met elkaar
gerelateerd zijn zoals bij elke schaal. Hieruit volgt dan
((1-kn)/kn)(1±r)n=1
(1-kn)/kn=(1±r)-n
(1-kn)=kn(1±r)-n
1=kn+kn(1±r)-n
kn(1+(1±r)-n)=1
kn=1/(1+(1±r)-n)
Dit is niet anders dan
((-1+kn)/kn)(1±r)n=-1
(-1+kn)/kn=-(1±r)-n
(-1+kn)=-kn(1±r)-n
-1=-kn-kn(1±r)-n
kn(1+(1±r)-n)=1
kn=1/(1+(1±r)-n)
Interpretatie
De schaalfactor komt van de intensiteiten (cumulaties) van de
eenheden kn en (1-kn). Een willekeurig proces
zal ofwel een intensiteit (van een eenheid) exponentieel doen
toenemen of exponentieel doen afnemen. Wanneer we een begrensd proces
willen modelleren hebben we daarom twee simultane processen nodig en
die interactie moet gemodelleerd worden door een product en genereert
dus onvermijdelijk een schaal. Wanneer de interactie als een
beperking moet gemodelleerd worden (omdat een beperking effectief
vastgesteld wordt), moet ook de schaal beperkt worden, dus als de
intensiteit van de eenheid in het ene proces toeneemt, dan moet de
intensiteit in het tweede proces ook toenemen, en omgekeerd. Dat is
de betekenis dat de twee eenheden door een constante schaalfactor met
elkaar verbonden zijn. Maar de twee eenheden zijn ook door een som
met elkaar verbonden. De som kn+(1-kn)
modelleert 1 en 1 wordt ook door de verhouding ((1-kn)/kn)(1±r)n=1
gemodelleerd. We kennen dat model als de relatie die bestaat tussen
een punt uit een
eerste generatie verschil (verschil tussen twee toestanden) en een
tweede generatie verschil (verschil tussen twee verschillen van
toestanden). De som van beide verschillen is een welgevormde
haakuitdrukking die een intensiteit kan hebben (eenheid die enkel als
een 3&1 som te modelleren is), het product van beide verschillen
is een ervaren toestand die een intensiteit kan hebben (en de rol
speelt van een effectief waargenomen spoor) en die we gemodelleerd
hebben als de intensiteit van één bit.
De som van een eerste generatie verschil en een tweede
generatieverschil is dus de eenheid van een onderscheiding H in het
getallendomein (de som kn+(1-kn) modelleert 1).
Het product van een eerste generatie verschil en een tweede
generatieverschil is dus de eenheid van een projector (<>⊕T),
een dubbelgetal in het getallendomein (het product ((1-kn)/kn)(1±r)n
modelleert ook 1).
Dat
zijn twee verschillende eenheden omdat ze invariant zijn onder
verschillende operaties
Het eerste generatie verschil en het tweede generatieverschil zijn
hiermee de twee verschillende maar fundamentele en abstracte
“onderliggende” eenheden van het patroon (<>⊕T), een
ervaren toestand. Dat is het patroon van de eenheid van een
processnelheid. Op basis van die “onderliggende” eenheden kan
gelijk welke werkelijkheid opgespannen worden die dat soort sporen
achterlaat. We hebben daarenboven aangetoond
dat ze als “snelheid” en “versnelling” kunnen geïnterpreteerd
worden, maar ook als “stroom” en “spanning”, maar nog
fundamenteler als “energiedensiteit”
en “vermogendensiteit”.
De schaal die we verbinden aan die twee eenheden die met elkaar
verbonden zijn in die interpretatie noemen we in de standaard taal
een weerstand. De schaalfactor Rn zullen we dus een
weerstand kunnen noemen. De weerstand is de verhouding tussen de twee
eenheden en is dus de onvermijdelijk derde eenheid. Voorbeelden zijn
een elektrische weerstand (kwantificeert de schaal tussen stroom en
spanning), een schokdemper (kwantificeert de schaal tussen kracht en
snelheid), wrijving tussen twee oppervlakken (we onderscheiden een
statische wrijving en een kleinere dynamische wrijving, kwantificeert
de schaal tussen kracht en snelheid), visceuze wrijving (afschuiving
in vloeistoffen, kwantificeert de schaal tussen kracht en snelheid),
bulkviscositeit (bij vervormbare gassen en vloeistoffen onderscheiden
we een statische viscositeit en een kleinere dynamische viscositeit,
kwantificeert de schaal tussen druk en debiet).
Positieve versus negatieve weerstand
Het hele onderzoek is het gevolg van de hypothese dat een
eigenwaarde k een entiteit kan zijn en dus positief moet zijn en
kleiner dan 1. Deze entiteit kan wel een intensiteit hebben en deze
kan gelijk zijn aan 1 of groter dan 1 en die intensiteit kan toenemen
of afnemen in een cumulatie. Exact hetzelfde geldt voor de
eigenwaarde (1-k). Dit leidt tot de onvermijdelijke conclusie dat die
intensiteit enkel een schaalfactor kan zijn, een schaalfactor die
zichtbaar wordt in de verhouding (1-kn)/kn,
verhouding die de schaalfactor Rn bepaalt die, evenals kn,
een proces kan karakteriseren. Maar we moeten het verschil tussen kn
en Rn goed begrijpen: beide zijn ze variabel, maar
verschillen in wat ze modelleren: kn karakteriseert een
niveau in een tralie, en elke mogelijke kn kunnen we
gebruiken als eigenwaarde van een proces met een verdubbelingstijd of
halveringstijd van een cumulatie die de intensiteit karakteriseert
van de eenheid die de cumulatie, namelijk het gedrag van dezelfde
eenheid, meemaakt. Exact hetzelfde geldt voor de eigenwaarde (1-kn).
Rn karakteriseert de onvermijdelijke relatie tussen de
twee deel-eenheden van de eenheid ((1-kn)/kn).
Deze relatie is Rn=kn/(1-kn). Zowel
kn als (1-kn) modelleren de interactie van twee
processen van positieve feedback omdat we daarmee eenheden kunnen
modelleren (die niet kunnen gehalveerd worden). Maar positieve
feedback processen hebben ook een richting: naar meer positief ofwel
naar meer negatief. Enkel wanneer beide processen in dezelfde zin
toenemen (beide in de positieve zin of beide in de negatieve zin)
ontstaat een positieve Rn als verhouding. Een negatieve Rn
ontstaat als de zinnen van de positieve feedback tegengesteld zijn.
Aangezien het positieve feedback processen moeten zijn, zijn we met
zowel kn als (1-kn) entiteiten aan het
modelleren. Dat betekent dat, voor één bepaalde kn, het
aantal soorten die elkaar uitsluiten (en dan als toestanden kunnen
gemodelleerd worden) niet verandert, de intensiteit van die
toestanden wel (er zijn meerdere “individuen” of “realisaties”
van dezelfde toestand mogelijk, toestand die de entiteit is). Daarom
kunnen we ook een negatieve Rn veronderstellen om te
modelleren dat zowel kn als (1-kn) positieve
feedback processen karakteriseren, maar in tegengestelde zin.
De relatie ((1-kn)/kn)Rn=1 is
niet anders dan ((1-kn)/kn)(1±r)n=1
en hieruit hebben we kn=1/(1+(1±r)-n)
afgeleid. Hieruit volgt dat
1-kn=1-1/(1+(1±r)-n)=((1+(1±r)-n)-1)/(1+(1±r)-n)=((1±r)-n)/(1+(1±r)-n)=1/(1+(1±r)n).
Wanneer Rn=(1±r)n positief is, is ook
Rn-1=(1±r)-n positief. Dus (1-kn)
en kn zijn beide positief of beide negatief. Het eerste
geval begrenst kn want vereist dat 0<kn<1.
Het tweede geval (beide negatief) is onmogelijk want als kn<0
dan kan het niet dat (1-kn)<0, (1-kn) is dan
altijd een positief getal.
Een negatieve Rn kunnen we wel construeren uit
((1-kn)/kn)(1±r)n=-1, of dus
((-1+kn)/kn)(1±r)n=+1. Dit
modelleert dat, wanneer (1-kn) en kn beide
positief zijn, dan -(1-kn) en kn tegengesteld
teken hebben. Beide zijn positieve feedback processen maar dan in
tegengestelde richting.
We leiden dan af:
((-1+kn)/kn)(1±r)n=1
(-1+kn)/kn=(1±r)-n
(-1+kn)=kn(1±r)-n
-1=-kn+kn(1±r)-n
1=kn-kn(1±r)-n
kn(1-(1±r)-n)=1
kn=1/(1-(1±r)-n). De noemer zal nu negatief
kunnen zijn, nul of positief.
Uit kn=1/(1-(1±r)-n) leiden we dan af:
1-kn=1-1/(1-(1±r)-n)=((1-(1±r)-n)-1)/(1-(1±r)-n)=(-(1±r)-n)/(1-(1±r)-n)=-1/(1-(1±r)n)
Dus -1+kn=1/(1-(1±r)n). Ook deze noemer zal
negatief kunnen zijn, nul of positief.
Dus een 1-Rn of 1-Rn-1 die
negatief, nul of positief kan zijn, zal een discontinuïteit
veroorzaken wanneer de waarde van de noemer van kn=±1/(1-(1±r)-n)
en -1+kn=1/(1-(1±r)n) zich rond de nul bevindt
en dat is voor de waarde van n=0. Dat is dezelfde waarde voor kn
als voor 1-kn. De discontinuïteit kan de
waarnemingsresolutie modelleren van de eenheid kn en
onrechtstreeks dan ook van de eenheid (1-kn). De nul is te
interpreteren als de overgang van een negatieve naar een positieve
1-Rn en modelleert dan een situatie waarin de weerstand
minimaal is (zeer klein en onwaarneembaar kleiner), de grens van de
waarnemingsresolutie.
Hetzelfde patroon, maar met tegengesteld teken kunnen we afleiden
als volgt uit een vorm met (1+kn) in plaats van (1-kn):
(1+kn)/kn=(1±r)-n
(1+kn)=kn(1±r)-n
1=-kn+kn(1±r)-n
-1=kn-kn(1±r)-n
kn(1-(1±r)-n)=-1
kn=-1/(1-(1±r)-n). Voor een positieve Rn
is deze kn altijd negatief.
Hieruit volgt dan:
1+kn=1+(-1/(1-(1±r)-n))=(1-(1±r)-n)-1)/(1-(1±r)-n)=1/(1-(1±r)n)
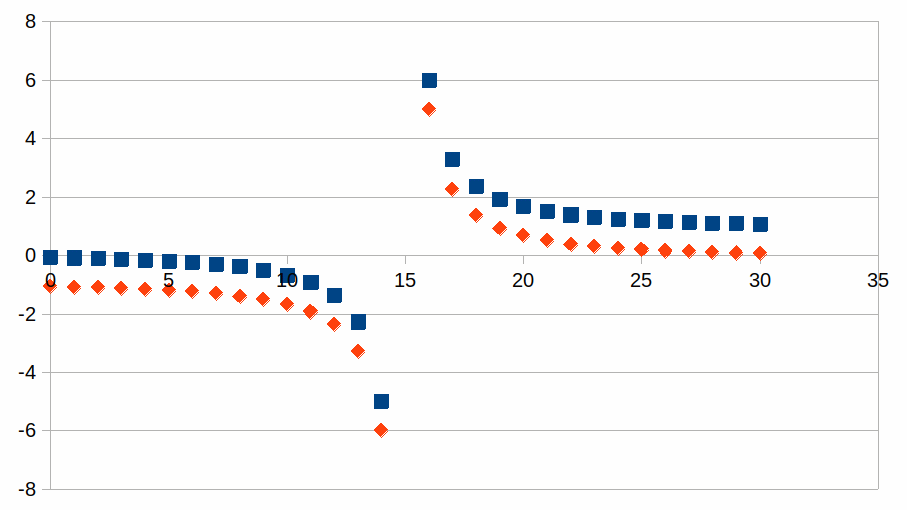
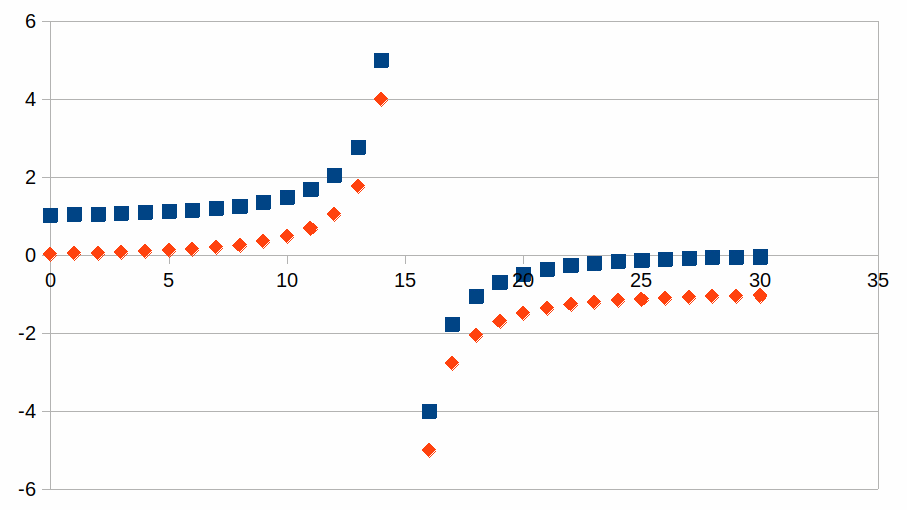
Een globaal overzicht met Rn=(1±0,2)n is te
geven in de tabel waarbij we ook de curven ofwel exponentieel of als
veelterm benaderen met de overeenkomstige determinatiecoëfficiënt.
Een veelterm van graad 4 blijkt reeds een goede benadering te zijn en
betere benaderingen zijn te bekomen voor een veelterm van een nog
hogere graad.
kn
|
Vierkant:
kn voor n van 0 tot 30
Ruit:
-1+kn voor n van 0 tot 30
|
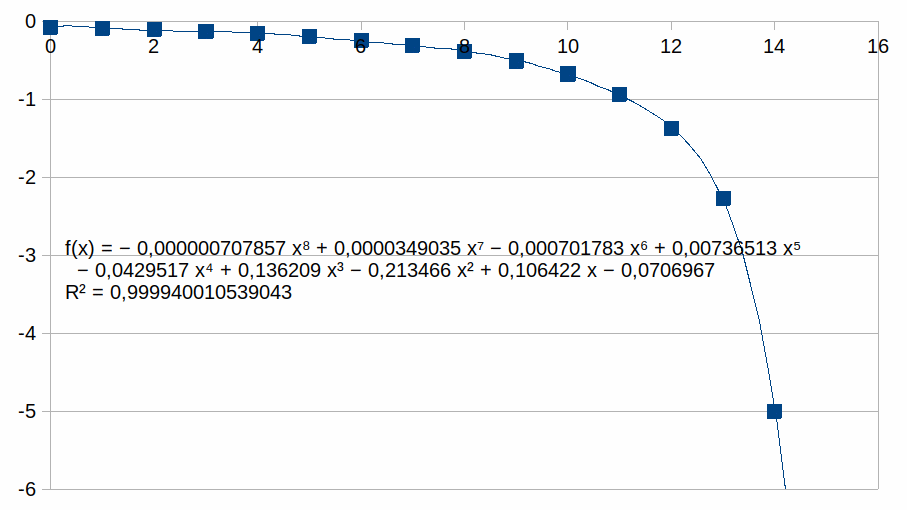
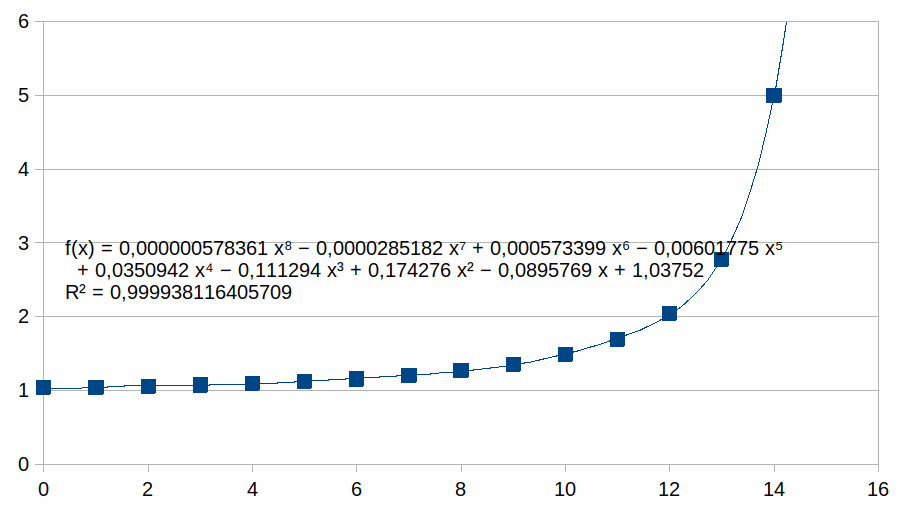
kn
voor n van 0 tot 15
|
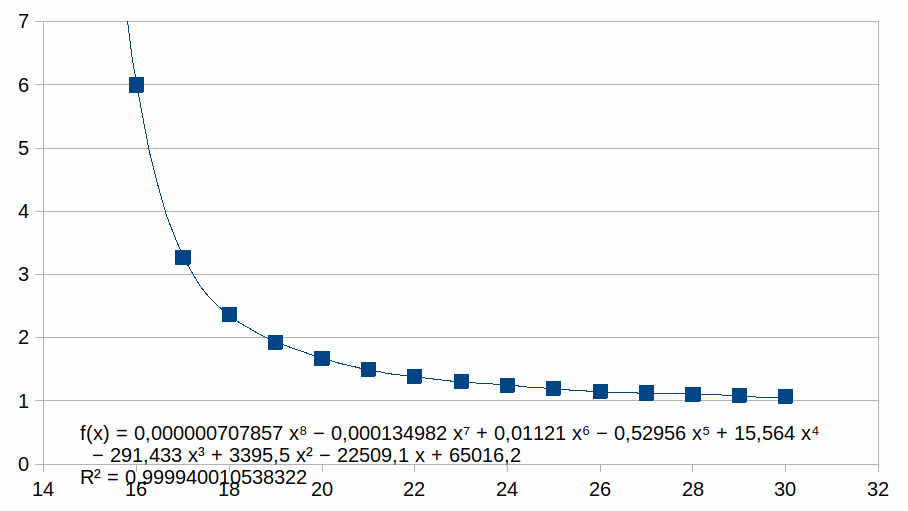
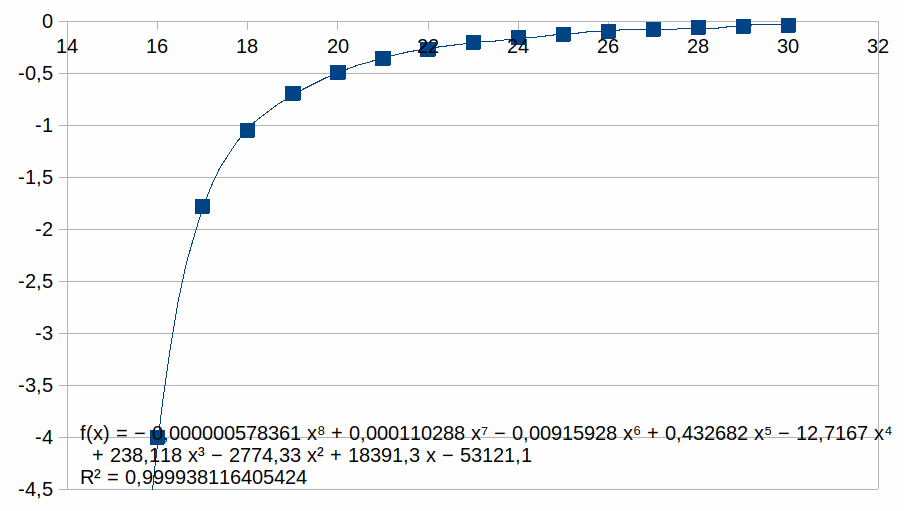
kn
voor n van 15 tot 30
|
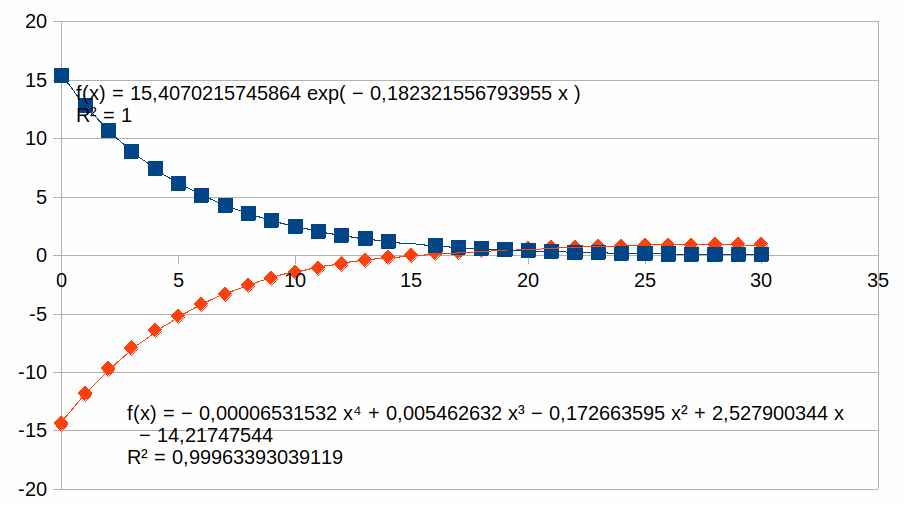
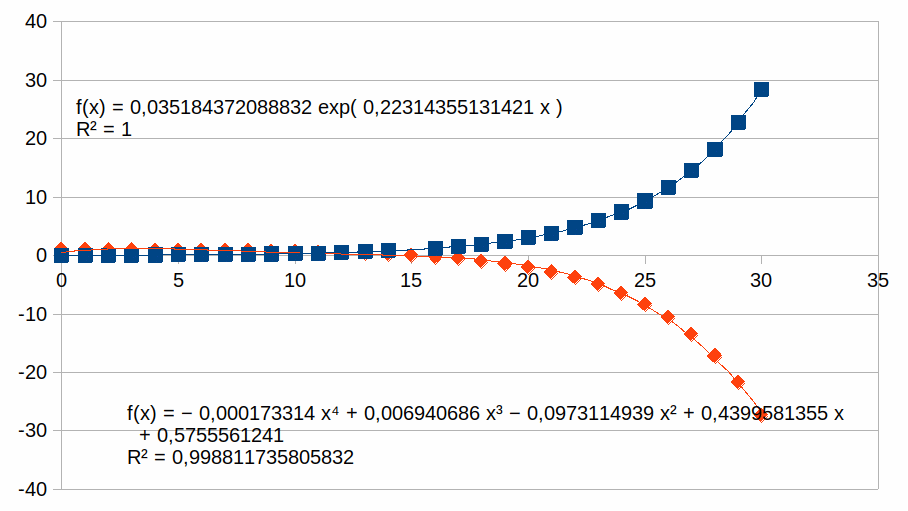
Vierkant:
-(1-kn)/kn
voor
n van 0 tot 30
Ruit:
1-Rn
voor n van 0 tot 30
|
1/(1-(1+0,2)-(n-15))
|
|
|
|
|
1/(1-(1-0,2)-(n-15))
|
|
|
|
|
Dit geeft de mogelijkheid om een andere interpretatie te geven aan
het Bose-Einstein model. Zoals
bekend is de Bose-Einstein verdeling niet begrensd. De
Bose-Einstein verdeling vinden we terug als we enkel sommen zouden
nemen in de verhouding, niet de verhouding van een verschil ten
opzichte van een som, dus als vergelijking bijvoorbeeld:
((1+kn)/kn)(1±r)n=1, in
tegenstelling met ((1-kn)/kn)(1±r)n=1.
We hebben dan het volgende afgeleid: kn=-1/(1-(1±r)-n).
Deze vergelijking is gekend als de beschrijving van de Bose-Einstein
verdeling.
Weerstand, resonantie en grondtoon
De discontinuïteit die we konden modelleren maakt de volgende
interpretatie mogelijk: <<de reductie en beperking (0<Rn<...)
van de weerstand van processen>> en <<het
ontstaan van nieuwe entiteiten>> zijn onlosmakelijk
verbonden met elkaar. Dit betekent niet dat er geen extra voorwaarden
nodig zijn om entiteiten te laten ontstaan. Maar als we erin slagen
om nieuwe entiteiten te herkennen dan zullen we er ook in slagen om
de weerstand van processen te verminderen, en als we de weerstand van
processen verminderen, dan zullen we ook kunnen zien dat nieuwe
entiteiten ontstaan. We merken dat processen die gecoördineerd
verlopen (al dan niet bewust gestuurd daartoe) altijd meer performant
zijn dan willekeurige interagerende processen. Coördinatie reduceert
weerstand, wat we duidelijk kunnen waarnemen bij diffusie
en convectie: wanneer deeltjes gecoördineerd bewegen is er ook
minder weerstand tegen beweging. De toename van entiteiten zien we in
de toename van het aantal onderscheidingen die we nodig hebben om
coördinatie te beschrijven.
In de context van het begrip “weerstand” spreekt men eerder
van resonantie in plaats van coördinatie. We illustreren dat met een
voorbeeld.
De wrijving tussen tektonische platen die, als de energie vrij
komt, een onheilspellend geruis produceert vinden we ook als de
wrijving tussen spanten, wrijving die ook geluid produceert. Dit
geluid is betekenisvol zoals men vroeger wist: “zolang je het
(houten) schip ritmisch hoort kraken, is er geen probleem”. De
analogie met wrijving kan nog verder doorgetrokken worden want
bijvoorbeeld de wrijving tussen snaar en strijkstok geneert muziek.
Weerstand en wrijving is onvermijdelijk en kwantificeert de relatie
tussen twee eenheden. Resonantie
is onvermijdelijk omdat een verhouding (en dus een schaal) ook altijd
een hoek (en dus een fase) genereert. Om de energie die vrijkomt te
kunnen waarnemen moet men op zoek gaan naar de meest gepaste schaal
en dan zouden we kunnen spreken van een grondtoon en boventonen.
Misschien moeten we op zoek gaan naar de grondtonen in de meest
langdurende processen (dus in een ecologie), grondtonen die
gegenereerd worden door wrijving maar die als harmonisch kunnen
ervaren worden door sommige agentia-in-context. “Zolang je een
ecologisch geheel ritmisch hoort kraken, is er geen probleem”.
Weerstand en chaos
In de praktijk merken we dat weerstand en warmte(straling)
onlosmakelijk verbonden zijn met elkaar, dus: zolang er geen nieuwe
entiteiten ontstaan zullen processen warmte genereren. Wanneer we de
productie van warmte willen beperken zullen nieuwe entiteiten moeten
kunnen ontstaan. In de praktijk merken we dat de productie van warmte
en de irreversibiliteit van processen onlosmakelijk verbonden zijn
met elkaar, dus: processen kunnen reversibel gemaakt worden door
entiteiten te laten ontstaan en te laten verdwijnen (hun intensiteit
buiten de waarnemingsgrens te krijgen) in telkens weer andere
configuraties (coördinaties) van deelprocessen met telkens een
andere eigenwaarde kleiner dan 1.
Processen met een eigenwaarde k groter dan 1 (en dus wanneer vanaf
de eerste stap al iets meer dan één eenheid of meerdere eenheden
kunnen ontstaan), modelleren “meer dan spontane (k=1) processen”.
We tonen aan dat dit onvermijdelijk verbonden is met het
ontstaan van chaos. Warmte begrijpen we als een chaotische
dynamiek. De tweede wet van de thermodynamica die zegt dat entropie
alleen maar kan toenemen is dus alleen maar geldig als er geen nieuwe
persistente entiteiten ontstaan die bestendigd worden door negatieve
feedback. Een warmtebad is noodzakelijk en maakt sommige entiteiten
mogelijk. Een warmtebad is niet voldoende om die entiteiten te laten
ontstaan en ze een rol te geven in een spontaan proces dat met andere
processen kan interageren. Het creëren van nieuwe entiteiten is een
voldoende voorwaarde om de aspecten die dit in het verleden mogelijk
gemaakt hebben te
(re)construeren. We kunnen dit enkel maar proberen en achteraf
vaststellen dat het gelukt is, als we er ook zouden in slagen om die
entiteiten voldoende persistent te maken.







