We hebben gezien dat een matrix impliciet een laatst toegevoegde onderscheiding modelleert. Een matrixproduct is associatief maar in het algemeen niet commutatief. Dat herkennen we ook bij het creatief product met een laatst toegevoegde onderscheiding die altijd dezelfde waarde heeft. Een algemeen creatief product is niet commutatief en niet associatief.

Een matrix is een structuur, is een eenheid die een intensiteit kan krijgen. De commutativiteit van eenheid en intensiteit die bij een getalproduct nog beschikbaar is, is bij een matrix niet meer beschikbaar. We onderzoeken nu wat dit betekent bij de machtsverheffing. De machtsverheffing is in het algemeen niet commutatief en evenmin associatief. Een laatst toegevoegde onderscheiding herkennen we ook als de intensiteit van het grondtal dat gekozen wordt om gelijk welk getal als exponent te kunnen voorstellen zodanig dat we twee soorten exponentiële inversen van een getal kunnen modelleren. Al deze inzichten gebruiken we nu om intensiteiten van eenheden die matrices zijn beter te begrijpen.

Elk getal kan geschreven worden als het exponentieel getal e tot een zekere exponent.

Er geldt:

eⁿ=1+(1/1)(n)¹+(1/2!)(n)²+(1/3!)(n)³+(1/4!)(n)⁴+…

Dus er geldt ook voor het dubbelgetal (eⁿ -1)

(eⁿ -1)=(1/1)(n)¹+(1/2!)(n)²+(1/3!)(n)³+(1/4!)(n)⁴+…

Dit is een som van eenheden n¹, n², n³, … telkens met een intensiteit (een inverse faculteit), hoe meer termen gekozen worden, hoe beter het getal benaderd wordt.

Er geldt dus ook met n=1:

e=e¹=1+(1/1)(1)¹+(1/2!)(1)²+(1/3!)(1)³+(1/4!)(1)⁴+…

Dus (e-1)=(1/1)(1)¹+(1/2!)(1)²+(1/3!)(1)³+(1/4!)(1)⁴+…

We zien hier het dubbelgetal (e-1). We hebben dit getal (e-1)=1,718281828459... in het haakformalisme geconstrueerd door een m te kiezen tussen 0 en 1 en dan moet <m> een niet te kiezen getal zijn, dit is het unieke getal (e-1)=1,718281828459.…

Dus (e-1) interpreteren we als een som van eenheden 1¹, 1², 1³, … telkens met een intensiteit, hoe meer termen, hoe meer gewogen eenheden gekozen worden, hoe beter het getal (e-1) benaderd wordt.

Met n=-1 wordt de reeks 1/e=e^-1=1-(1/1)(1)¹+(1/2!)(1)²-(1/3!)(1)³+(1/4!)(1)⁴+… dus (1/e -1)=-(1/1)(1)¹+(1/2!)(1)²-(1/3!)(1)³+(1/4!)(1)⁴+…

Er geldt nu eveneens dat elke matrix kan geschreven worden als het exponentieel getal e tot een zekere exponent A die een vierkante matrix is:

e^nA =1+(1/1)(nA)+(1/2!)(nA)²+(1/3!)(nA)³+(1/4!)(nA)⁴+… dus e^nA -1=(1/1)(nA)+(1/2!)(nA)²+(1/3!)(nA)³+(1/4!)(nA)⁴+… en in (e^nA -1) is 1 natuurlijk de eenheidsmatrix.

We kunnen nu een aantal veronderstellingen maken over de vierkante matrix A.

Matrix A is een projector

Een projector is idempotent voor de operatie die erop uitgevoerd wordt. Voor een matrix nemen we het product van matrices als operatie. We veronderstellen dus matrices als projectoren A²=A, dus A³=A²A=AA=A²=A enz… Projectoren vervullen de functie van eenheid.

Een voor de hand liggende projector is de eenheidsmatrix, minder voor de hand liggende projectors zijn de genormaliseerde operatoren die we vormen in het 1-splitsing universum door het uitwendig product van een vector met zichzelf. Met het matrix product van deze projectors kunnen we dan de metriek in een tralie berekenen als de afstand (of inwendig product) tussen de projectors en dat geheel getal kan geïnterpreteerd worden als de intensiteit van elke projector.

In e^nA =1+(1/1)(nA)+(1/2!)(nA)²+(1/3!)(nA)³+(1/4!)(nA)⁴+… veronderstellen we nu dat A een projector is

e^nA =1+(1/1)n(A)+(1/2!)n²(A)+(1/3!)n³(A)+(1/4!)n⁴(A)+…

e^nA =1+((1/1)n+(1/2!)n²+(1/3!)n³+(1/4!)n⁴+…)(A)

e^nA =1+(1+(1/1)n+(1/2!)n²+(1/3!)n³+(1/4!)n⁴+…)(A)-(A)

e^nA =1+(eⁿ)(A)-(A)

e^nA =1-(A)+eⁿ(A)

(A)(1-eⁿ)=1-e^nA of ook e^nA -1=(eⁿ-1)(A)

Matrix A heeft een waarde

A²=+1=A

Het is duidelijk dat e^nA -1=(eⁿ-1)(A) ook geldt voor A als de 1x1 matrix: het getal 1. Dus eⁿ kunnen we nu interpreteren als de variabele en 1 als de “beginvoorwaarde” zodat (eⁿ-1)=(x-x₀) en als we n interpreteren als een stap, monotoon toenemend zoals een laatst toegevoegde onderscheiding, dan is de variabele een som van eenheden n, n², n³, … telkens met een intensiteit, hoe meer stappen gekozen worden, hoe beter het getal e benaderd wordt. Noteer dat e⁺¹ bij steeds grotere n benaderd wordt door (1+1/n)ⁿ en e^-1 wordt benaderd door (1-1/n)ⁿ. Dus voor een n die steeds kleiner gekozen wordt geldt e=(1+n)^1/n en dus: eⁿ=1+n dus in de limiet voor steeds kleinere n: eⁿ-1=n. En gelijkaardig geldt dus ook (1-n)^1/n=1/e of dus 1-n=e^-n. Deze laatste zijn dus benaderingen van het getal 1.

Het is deze veronderstelling die aan de basis ligt van de technieken uit de analytische integratie.

A²=-1

Het kwadraat van een matrix kan ook waarde -1 hebben zonder dat A een waarde heeft (waarde +1 of waarde -1). Dit levert een volledig nieuwe interpretatie op voor de exponent.

In e^nA =1+(1/1)(nA)+(1/2!)(nA)²+(1/3!)(nA)³+(1/4!)(nA)⁴+… drukken we nu uit dat A niet bekend is maar A²=-1.

Er geldt:

A=+A

A²=-1

A³=A*A²=-A

A⁴=A*A³=-A²

A⁵=A²*A³=+A

enz… elke term kunnen we dus uitdrukken ofwel in de eenheid A, ofwel in de eenheid A².

Hiermee kunnen we e^nA=Σ_k=0 ^k=∞(1/k!)(nA)^k herschrijven als volgt:

e^nA =1+(1/1)(nA)+(1/2!)(nA)²+(1/3!)(-n²(nA))+(1/4!)(-n²(nA)²)+(1/5!)(n⁴(nA))+(1/6!)(n⁴(nA)²)-(1/7!)(n⁶(nA))-...

=1+(1)(nA)+(1/3!)(-n²(nA))+(1/5!)(n⁴(nA))+...+(1/2!)(nA)²+(1/4!)(-n²(nA)²)+(1/6!)(n⁴(nA)²)-(1/7!)(n⁶(nA))-...

=1+((1)+(1/3!)(-n²)+(1/5!)(n⁴)-(1/7!)(n⁶(nA))-...)(nA)+((1/2!)+(1/4!)(-n²)+(1/6!)(n⁴)-…)(nA)²

=1+((n)+(1/3!)(-n³)+(1/5!)(n⁵)-(1/7!)(n⁶(nA))-...)(A)+((1/2!)n²+(1/4!)(-n⁴)+(1/6!)(n⁶)-…)(A)²

=1+(sin(n))(A)+(1-cos(n))(A)²

Dit maakt onmiddellijk duidelijk dat de mogelijkheid om rotaties te modelleren, en dus variatie die beschreven wordt door slechts één parameter n, de rotatiehoek, rechtstreeks afhangt van de waarde van het kwadraat van matrix A.

De meest eenvoudige matrix waarvan het kwadraat de negatieve eenheid is, is een van de 2x2 matrices. We nemen nu het volgende isomorfisme van het één onderscheiding universum en beschouwen de termen nu als gewone getallen.

υν=-νυ, νυ^T=νυ^-1=υν, (νυ)(υν)=ε, (-ε+νυ)²=ε²-2νυ+νυ²=ε-2νυ-ε=2νυ, (-ε+νυ)(-ε+υν)=2ε. Hierbij moeten we ook 2 als een getal beschouwen dat opgebouwd wordt vanuit de intensiteiten die zouden kunnen toegewezen worden aan ε en νυ afzonderlijk. Normalisatie zorgt er voor dat (-ε+νυ) en (-ε+υν) elkaar invers zijn. De determinant zal op dezelfde manier berekend worden als dat getal. De determinant van -ε+νυ blijkt inderdaad 2 te zijn, en dus normalisatie is te bekomen als we alle termen delen door de wortel van 2, de determinant wordt dan gelijk aan 1.

We nemen nu νυ als de matrix A en berekenen νυ=νυ, νυ²=-ε, νυ³=-νυ, νυ⁴=ε, νυ⁵=νυ, νυ⁶=-ε, νυ⁷=-νυ, enz… De algemene formule 1+(sin(n))(A)+(1-cos(n))(A)² wordt dan: 1+(sin(n))(νυ)+(1-cos(n))(-ε)=cos(n)+(sin(n))(νυ) en dit is niet anders dan de formule van Euler eⁱⁿ=cos(n)+i(sin(n)) en de basis eenheid kan als het complex getal 1+i beschouwd worden.

We zullen de laatst toegevoegde onderscheiding en de extrema in een 1-splitsing een intensiteit geven, dan kunnen we ook voor de twee eenheden (de laatst toegevoegde onderscheiding en de extrema) verschillende intensiteiten veronderstellen.

Een algemene rotatie kan dus voorgesteld worden als

We merken op dat we n (de rotatiehoek) vrij kunnen kiezen. Voor elke keuze van n tussen 0 en 2π is het resultaat van de algemene formule een som van intensiteiten van de twee basisvectoren van dit universum, namelijk de intensiteit van <<>> en de intensiteit van a. Dus de intensiteit van de laatst toegevoegde onderscheiding kan niet los gezien worden van de intensiteit van de extrema en dat is dan weer geen vrije keuze meer. Dat is exact de beperking die we ook op een andere manier kunnen modelleren als een hoek.

(nA)³=n²(-nA) als een 3x3 matrix

We merken op dat νυ een spoorloze matrix is. We construeren nu een anti-symmetrische spoorloze 3x3 matrix als 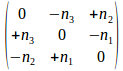en deze zal een heel specifieke kolom matrix transformeren in de nulvector als kolom matrix 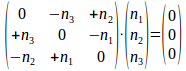. En dus, met 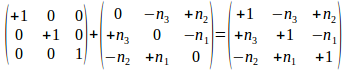, geldt 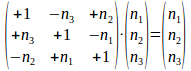. Die specifieke 3x3 operator laat de kolom vector invariant.

We berekenen nu het kwadraat en de derde macht van deze spoorloze 3x3 matrix A.

Het kwadraat is .

De derde macht is: .

De derde macht is dus niet anders dan .

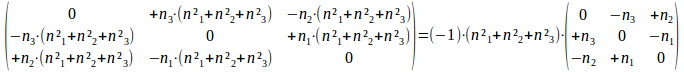Dat betekent dat de derde macht gelijk is aan (-1)n²(A) onder de voorwaarde dat we alle getallen vermenigvuldigen met (n²₁+n²₂+n²₃)^-1/2 en dat we kiezen dat n²=((n²₁+n²₂+n²₃)^-1/2)²=(n²₁+n²₂+n²₃). Hierbij kunnen we de hoek n dus niet meer vrij kiezen omdat het kwadraat een som van drie kwadraten moet zijn (voor de gehele positieve getallen wordt de beperking gegeven door een stelling van Legendre die zegt dat het getal n dan verschillend moet zijn van 4^a(8b+7) voor positieve gehele getallen a en b).

De algemene formule e^nA=1+(sin(n))(A)+(1-cos(n))(A)² wordt dus:

Of dus:

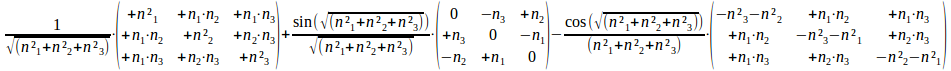
We hebben begrepen dat een rotatiehoek de intensiteit is van een laatst toegevoegde onderscheiding. Nu blijkt dat de keuze voor drie telbare parameters ook een bepaalde intensiteit van laatst toegevoegde onderscheiding vastlegt, en omgekeerd een keuze van hoek verschillende mogelijke drie telbare parameters vastlegt. Het is die surjectieve relatie en dus beperking die zorgt voor de onvermijdelijkheid van onze driedimensionale werkelijkheid.

Commutatieve matrices

Voor x en y getallen geldt de volgende relatie: e^x×e^y=e^(x+y). De relatie die geldt voor getallen x en y blijkt voor n*n matrices X en Y enkel op te gaan als ze commutatief zijn. Commutativiteit hebben we begrepen als eenheid en intensiteit die elkaars rol kunnen innemen.

Projectoren zijn commutatief.

Orthogonale matrices zijn commutatief.

Met commutatieve matrices kunnen we een product door een som te vervangen.