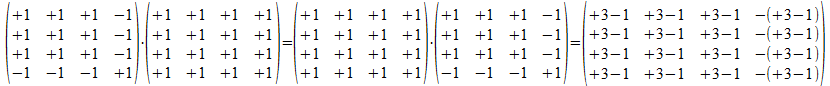
We hebben aangetoond dat een genormaliseerde projector die met het matrix product vermenigvuldigd wordt met zichzelf idempotent is, er geldt dan dat P2=P. Een onmiddellijk gevolg hiervan is dat dit ook zal gelden voor Pn=P want bijvoorbeeld P3=P2*P=P*P=P2=P.
Verschillende projectoren kunnen uiteraard ook met elkaar vermenigvuldigd worden. Hierbij ontstaan getallen die gerelateerd zijn aan de structuur waarin de beide projectoren gedefinieerd zijn.
Als voorbeeld geven we in twee onderscheidingen de vermenigvuldiging van P(++++) met P(-+++), beide punten hebben drie gelijke bits en één verschillende bit. De getallen 3 en 1 zullen we in de uitwerking van het product expliciet niet verbergen. We zullen de vermenigvuldiging voorstellen als P(++++) * P(-+++) en we bewijzen in één trek dat P(-+++) * P(++++)=P(++++) * P(-+++).
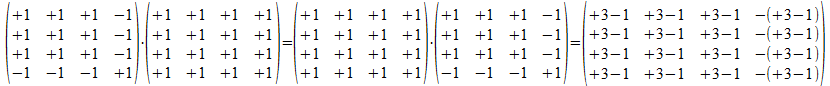
We zien (+3-1) ontstaan als gemeenschappelijke factor. We kunnen dit resultaat terug vermenigvuldigen met een van beide projectoren.
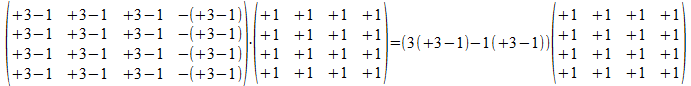
en
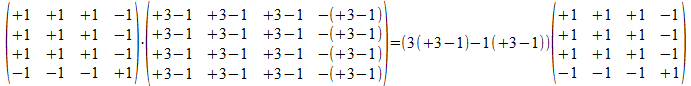
Dit betekent dus dat P(-+++)*P(++++) * P(-+++)=α*P(++++) en P(++++)*P(-+++) * P(++++)=α*P(-+++) waarbij α enkel afhangt van de onderlinge relatie van beide operatoren. Dit is een reëel getal dat kan geformuleerd worden in het aantal bits die overeenkomen en het aantal bits die verschillen, exact ook die aantallen die het inwendig product opbouwen. We zien ook dat het niet anders kan dat α gelijk is aan het spoor van de matrix die het product van beide projectoren geeft.
Om dat te illustreren geven we nog een aantal voorbeelden:
P(-+++)*P(+-+-)=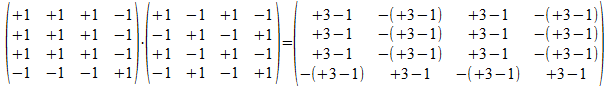
P(+-+-)*P(-+++)=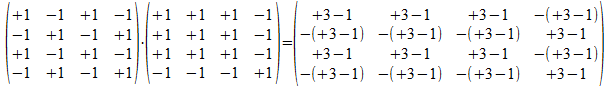
We merken op dat commutativiteit voor deze projectoren niet geldt.
P(-+++)*P(++--)=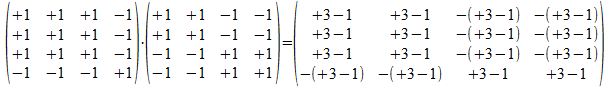
P(++--)*P(-+++)=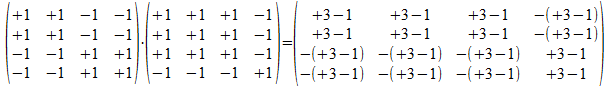
We merken op dat commutativiteit voor deze projectoren niet geldt.
P(+-+-)*P(++--)=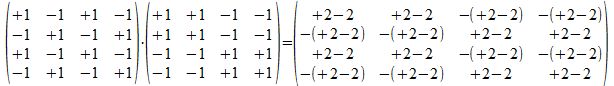
P(++--)*P(+-+-)=
De laatste voorbeelden maken duidelijk dat P(+-+-)*P(++--)=P(++--)*P(+-+-)=0. Het matrix product van de projectoren op centraal niveau is dus commutatief en gelijk aan de nulvector.
We kunnen ook controleren dat geldt dat P(+++-)*P(++-+)=P(++-+)*P(+++-)=0. Het matrix product van de projectoren op atoomniveau in twee onderscheidingen is dus commutatief en gelijk aan de nulvector. Hieruit kunnen we besluiten dat dit zal gelden voor alle projectoren waarvan het inwendig product gelijk is aan nul. Dit zijn dan orthogonale projectoren.
Het eerste voorbeeld maakt daarentegen duidelijk dat P(-+++)*P(++++)=P(++++)*P(-+++). Blijkbaar is P(++++) commutatief met alle projectoren.