Thermische energie is een belangrijke factor op onze aardbol. Sinds we het vuur beheersen en thermische energie in andere energievormen kunnen omzetten (denk maar aan stoomturbines en ontploffingsmotoren) is de maatschappij rond thermische energie georganiseerd, en dat ondanks het feit dat dit een zeer chaotische vorm van energie is. Sinds we zelf macromolecules kunnen synthetiseren en onderzoeken zijn we beter gaan begrijpen hoe trillingen van molecules temperatuur afhankelijkheid zijn. Zo zijn we ook meer en meer het ontstaan van het leven gaan begrijpen vanuit zeer geleidelijke afkoeling van een moleculaire soep waarin verbindingen tussen molecules op een bepaald moment “bevroren werden”. We zijn gaan beseffen dat we zelfs in staat zijn om een kracht te genereren wanneer we die nieuwe vrijheidsgraden als hypothese aannemen. Die kracht wordt de entropische kracht genoemd omdat ze rechtstreeks met temperatuur gerelateerd is. We stellen ons die kracht als volgt voor: veronderstel een molecule als een lange keten van componenten in een medium van kleinere molecules (water, gas enz…) en veronderstel dat een evenwicht bereikt is op een bepaalde temperatuur. De entropie is dan maximaal, er is nog steeds verandering waarneembaar maar we slagen er niet meer in om die te ordenen, wat gebeurt is onvoorspelbaar geworden. We kunnen echter de mogelijke configuraties toch nog in categorieën onderbrengen en dan waarnemingen verrichten. Die categorieën zijn dus niet individuele molecules als entiteiten maar soorten configuraties van molecules die we als entiteiten aannemen en die meer of minder waarschijnlijk zijn. Dat is enkel afhankelijk van onze creativiteit om ons die configuraties in te beelden om ze dan te kunnen realiseren in een meetopstelling. We kunnen bijvoorbeeld veronderstellen dat een lange molecule gemiddeld zich meer in bepaalde ruimtelijke configuraties bevindt en dat het heel onwaarschijnlijk is dat de molecule volledig uitgestrekt kan waargenomen worden. We kunnen die hypothese dan proberen te realiseren: we kunnen proberen om de molecules in die onwaarschijnlijke configuratie te brengen. Daartoe zullen we een vermogen nodig hebben. Wanneer we daarin slagen zouden we de nieuwe configuratie kunnen bevriezen door de temperatuur van het medium te verlagen zodanig dat spontane bewegingen niet meer mogelijk zijn en een nieuw evenwicht op een bepaalde temperatuur bereikt wordt. We kunnen dat als volgt demonstreren met een kunststof: we warmen deze op zodanig dat de viscositeit afneemt. Dan kunnen we met weinig moeite de vorm in een andere configuratie brengen (we warmen bijvoorbeeld korrels op tot een vloeistof die we in een matrijs injecteren en we kunnen de vorm van de molecules door stroming beïnvloeden). Door snelle afkoeling kunnen we die nieuwe configuratie (de vorm in de matrijs) dan vastleggen in de kunststof. Een ander voorbeeld vinden we bij textielvezels (die we in gestrekte toestand willen gebruiken); als de vezel zou gekreukt worden en dus in een andere configuratie gedwongen wordt, dan kunnen we hem terug strekken door opwarmen (bijvoorbeeld door het textiel te strijken met een strijkijzer). De voorbeelden tonen dat, als we de temperatuur weer verhogen, de configuratie van de molecule terug verandert en deze beweging kan een kracht opwekken. Maar ook zonder met de temperatuur te variëren zouden we die onwaarschijnlijke configuratie kunnen bevriezen door reactie met andere lange molecules, waarbij we dan een grotere macromolecule maken waarin dat oorspronkelijk stuk molecule niet meer de vroegere evenwichtstoestand kan innemen en dus zodanig dat “een gedrag rond evenwicht” zelfs niet meer mogelijk wordt. Een voorbeeld hiervan zijn thermoharders en kunststoffen die door menging met een andere kunststof uitharden. Het is dit laatste proces dat we herkennen als molecules zich in dynamische (levende) structuren organiseren: er ontstaat een coördinatie tussen delen van molecules zodanig dat ze een nieuwe moleculecomplex maken en die coördinatie kunnen we beschrijven in nieuwe categorieën die zelfs dynamisch kunnen zijn. De configuraties kunnen veranderen onder invloed van beperkte temperatuur schommelingen of andere energievormen. Als deze coördinatie cyclisch gebeurt (te meten in Hertz), zoals bijvoorbeeld bij de seizoenen, dan is het mogelijk dat een resonantie met andere processen mogelijk wordt, processen die vrije energie kunnen leveren.
Vermogen is fundamenteler dan energie. Vermogen kunnen we niet enkel beschouwen als de energie per stap in de tijd, maar kunnen we ook beschouwen als de energie of exergie per vrijheidsgraad. Het nuttig vermogen is exergie per “te ordenen eenheid van densiteit”, exergie per “te ordenen potentiaal”, exergie “per stap”. Vermogen is dus een energiedensiteit die we kunnen meten “onafhankelijk van tijd” maar afhankelijk van een andere monotone parameter. Vermogen kan een intensiteit hebben die stabiel blijft in de tijd maar die verandert in functie van die andere parameter, stel P. Vermogen kan geaccumuleerd worden tot energie “los van hoe dat met een klok gemeten wordt”. We kunnen ons dat voorstellen door de analogie met snelheid als densiteit van afstand in de tijd: een snelheid “onafhankelijk van tijd”, dus zonder dat we van een “voor” en een “na” kunnen spreken, noemen we de lichtsnelheid. Elektromagnetische straling is vermogen met parameter (de eenheid van de densiteit) verschillend van tijd, bijvoorbeeld energie per frequentie F (dus reciproque tijd). Zo is de energie van een foton gelijk aan hF (h is de constante van Planck) en het hele elektromagnetisch spectrum kunnen we klasseren zowel volgens oplopende energie van het foton, volgens de temperatuur van een zwarte straler, volgens golflengte en volgens frequentie.
Vermogen kunnen we dus ook accumuleren door het aantal onderscheidingen van een universum als maat te nemen (parameter P), aantal dat onvermijdelijk een kleinste aantal impliceert dat we kunnen kiezen (namelijk 1) en ook een grootste aantal impliceert dat we niet kunnen kiezen, dat enkel maar kan gebeuren (“de laatst toegevoegde onderscheiding” als grootste priemgetal, dus verschillend van 1, dus van het type 1+k).
Hieruit blijkt dat we ook temperatuur als willekeurig te kiezen parameter kunnen gebruiken. Temperatuur beschouwen we in de toegepaste wetenschappen als een monotone functie van de gemiddelde kinetische energie van de molecules in een bepaald materiaal (massa, volume enz...). We stellen ons voor dat de amplitude van elke trilling van een kleine molecule toeneemt, de wederzijdse afstand daardoor toeneemt zodanig dat het totale volume van alle molecules samen ook toeneemt. Dit leidt tot een relatieve toename van een volume per temperatuurstap en blijkt in eerste benadering lineair te zijn in één dimensie en materiaalafhankelijk. Temperatuur kunnen we dus ordenen en gebruiken als maat. Temperatuurverschillen zijn te ordenen en alle experimenten lijken te bevestigen dat het absolute nulpunt van temperatuur een zinvol begrip is, zelfs als het nooit zou kunnen bereikt worden. Door temperatuur als parameter voor de stap in een proces te nemen kunnen we een monotoon proces van afkoeling en simultaan opwarming modelleren: wanneer iets warmer is dan de context dan koelt het spontaan af en dan warmt de context spontaan op tot een evenwicht bereikt is waarbij alles dezelfde temperatuur heeft (het temperatuurverschil is zeer klein en onwaarneembaar kleiner). Alles staat dan op hetzelfde potentiaal (“het warmtebad”) en er is geen enkele gradiënt meer waar te nemen. Beide processen zijn van elkaar te onderscheiden maar niet te scheiden. De entiteiten die het proces meemaken zijn wel te onderscheiden: we maken een onderscheid tussen “wat de entiteit is die opwarmt” versus “wat de entiteit is die afkoelt”. Ze zijn met elkaar onvermijdelijk verbonden door de relatie “iets” versus “iets anders”. “Evenwicht” is niet anders dan “beschikken over alle relevante onderscheidingen om een universum te beschrijven”, dus beschikken over de onderscheidingen van “iets” en “iets anders” zodanig dat we die bepaalde invariantie kunnen modelleren.
De thermische energie is het commutatief product van temperatuur (een eerste eenheid) en entropie (een tweede eenheid). Wanneer we de temperatuur als stap nemen dan heeft de entropie het karakter van een vermogen, een snelheid, … een verhouding, een ratio, een processnelheid. Entropie is een getal dat we kunnen berekenen bij een transformatie van energie “bij een gekozen stap”. Entropie wordt hierin geaccumuleerd in een som, maar dat kan niet los van temperatuur gezien worden, zoals ook temperatuur niet los kan gezien worden van entropie. De ordening van temperatuur is zoals de ordening van tijd: we kunnen ervoor zorgen dat de temperatuur ofwel enkel toeneemt ofwel enkel afneemt, maar de ordening verdwijnt rond een lokaal evenwicht. Immers: het product van temperatuur en entropie is de energie in de evenwicht situatie en aangezien deze energie geen twee eenheden heeft omdat er geen te ordenen verandering meer is, kunnen we geen onderscheid maken tussen processnelheid en procesversnelling. Temperatuur (eerste eenheid) en entropie (tweede eenheid) zijn dus niet (eenheid1) en (eenheid2) met de parameter tijd (zoals de translatie verplaatsing x=ℂjvj (elastisch), en de translatie impuls p=ℂjFj (kinetisch)). Dus “iets” als “potentiële energie die omgezet wordt in kinetische energie of omgekeerd” is niet waarneembaar in evenwicht omdat er dan niets meer te ordenen valt in twee categorieën. Dit is een specifieke eigenschap van dit proces naar evenwicht en dit geven we dan ook een specifieke naam: de thermische energie. De thermische energie maakt het noodzakelijk om van een temperatuur te spreken en een entropie(stroom): de onvermijdelijke afname van de vrije thermische energie, die zich uit in een afname van temperatuur van iets en toename van de temperatuur van iets anders rond een lokaal evenwicht en waarvan de afname en toename “rond evenwicht” dan zo ongeordend gebeurt dat er niets anders meer mee aan te vangen is (de exergie is nul). Temperatuur kwantificeert blijkbaar een willekeurig verschil tussen iets en iets anders (wanneer iets opwarmt koelt iets anders af), een willekeur waaraan we niet kunnen ontsnappen.
Laten we de inzichten uit de ontwikkeling van het haakformalisme nu toepassen om het vermogen te interpreteren als de energie per “stap in temperatuur”, dus per Kelvin. We doen dat in twee stappen.
De meest universele manier om een toestand als getal in een tralie voor te stellen is 1/(1±n)m of dus (1±n)-m met (0<n<1). Hierin is m de intensiteit van de eenheid (1±n)-1 en een willekeurig rationaal getal is een voorbeeld van zo’n eenheid. Als exponent moet m een getal zijn en als intensiteit is het mogelijk daar een kleinste fractie van te nemen en dit te gebruiken als een schaal, zodanig dat 1/(1±n)m=(1±n)-m. Noem nu deze eenheid 1/T° en interpreteer dat als het operationeel kleinst mogelijk te meten temperatuurinterval (in Kelvin, het kleinste verschil met nul Kelvin). Dus m is niet anders dan een intensiteit van die praktische 1/T°. Maar dat betekent ook dat m een temperatuur moet zijn want een exponent moet dimensieloos zijn. Dus de exponent is nu een dimensieloze schaalfactor m/T°, de enige schaal naast de evidente 1, schaal die enkel afhankelijk is van het kleinst mogelijk te meten temperatuurinterval dat g bepaalt zodanig dat gm=mg of dus 1/(1±n)m=m(1±n)-1.
Eens we dit goed begrijpen, kunnen we ook inzien dat we m ook als een energie kunnen interpreteren. We moeten dan een “schaalcorrectie” aanbrengen die de fameuze Boltzmann constante genoemd wordt met dimensie Joule per Kelvin. Dus m is dan niet anders dan een intensiteit met de dimensie Joule met factor 1/kBT°, factor die dus ook de dimensie Joule heeft, zodanig dat de exponent dimensieloos is. Aangezien we het grondtal van een exponent vrij kunnen kiezen, zolang deze verschillend is van 1, en we dus het getal van Euler kunnen kiezen, kan de intensiteit van één toestand in de tralie ook voorgesteld worden als e-E/kBT°, wat we ook kunnen noteren als exp(-E/kBT°). Aangezien alle toestanden elkaar uitsluiten kunnen we optellen. Elke toestand wordt door een intensiteit gekarakteriseerd die we nu als een energie gemodelleerd hebben en alle toestanden hebben dezelfde schaal g (die hier het getal e is). Disjuncties (die als toestanden exclusieve disjuncties zijn) van toestanden met dezelfde waarde kunnen we noteren als Ei. Dan kunnen we dus bij één bepaalde evenwichtstemperatuur T° een zinvolle som veronderstellen als de som over i van al de termen e-Ei/kBT°. De i toestanden zijn de mogelijke toestanden bij een bepaalde temperatuur, de temperatuur meet dus onrechtstreeks een aantal onderscheidingen die relevant zijn voor een bepaald niveau in de tralie en het aantal toestanden is dan gegeven door een exponentieel verband, bijvoorbeeld i=2T°.
We interpreteren dat nu ook als Z=Σie-βEi met β de “coldness” gedefinieerd als β = 1/kBT°. De coldness is een energie. Is Ei >>> β dan is exp(-Ei/kBT°) weinig verschillend van 0 (zeer klein en onwaarneembaar kleiner). Is Ei <<< β dan is exp(-Ei/kBT°) weinig verschillend van 1. Dit maakt onmiddellijk duidelijk dat aan de voorwaarden voldaan wordt om een waarschijnlijkheid te berekenen.
De som Z is niet meer en niet minder dan de bekende Zustandssumme uit de statistische fysica (of zoals in het Engels gezegd wordt: de partition function). Als we de som Z gebruiken als de definitie van 1 uit de waarschijnlijkheidsleer (waarbij we dus de “indien…, dan…” constructie normaliseren), dan kunnen we de waarschijnlijkheid berekenen dat een gekozen energie(niveau) als toestand kan waargenomen worden, een waarschijnlijkheid die zich altijd tussen 0 en 1 bevindt.
Een manier om zich verschillende partities voor te stellen is door een tralie als een constructie van meerdere categorieën voor te stellen die elkaar uitsluiten ten opzichte van dezelfde disjunctie. Die categorieën zijn de energieniveaus en als deze zich op een even niveau bevinden dan kunnen ze met minder onderscheidingen opgespannen worden dan de tralie die door de toestanden opgespannen wordt. Zowel de toestanden sluiten elkaar uit als ook de energieniveaus die we voorstellen als disjuncties van toestanden, in dit geval moeten het exclusieve disjuncties zijn om te kunnen sommeren: verschillende sommen (dus verschillende partitie functies) kunnen gemaakt worden en de energieniveaus zullen in een andere distributie een andere waarschijnlijkheid van realisatie krijgen.
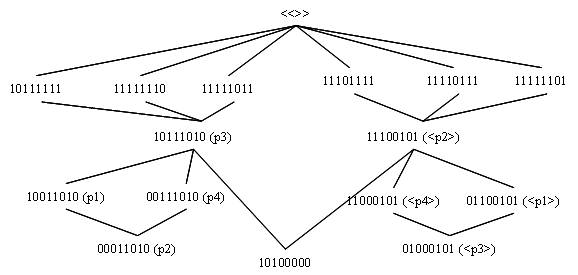
In een eerste voorbeeld hebben we voor de zes relevante toestanden twee energieniveaus verondersteld: p3 en <p2>, als voorbeeld van een M en M<> die elkaar uitsluiten. De relevante disjunctie is 10100000.

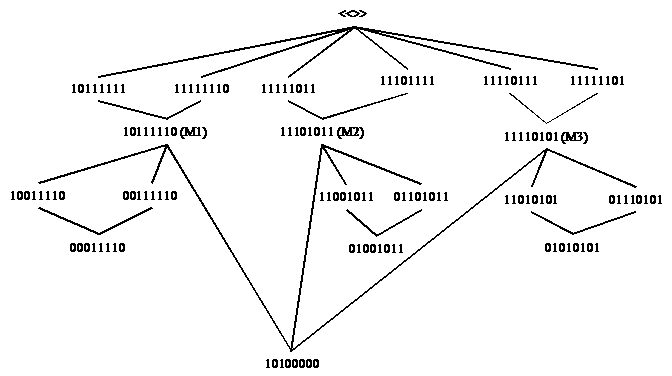
In een tweede voorbeeld hebben we voor de zes relevante toestanden drie energieniveaus verondersteld: M1, M2, M3, met dezelfde relevante disjunctie 10100000.
Dit
zijn ook de voorbeelden die we gebruikt hebben om de
relevante entropie te illustreren en de
kwantummechanische waarschijnlijkheid in het haakformalisme te
modelleren.
De energie van straling wordt gegeven door σT°4Ot met stralingsconstante σ (Watt/meter2.Kelvin4), temperatuur T° (Kelvin), oppervlak O (meter2), tijd t (seconde). We onderscheiden dus een vermogen1 (per tijd), een vermogen2 (per oppervlak), een vermogen3 (per T°4). Dit laatste is niet lineair maar hoe dan ook begrensd als verhouding. Van (de lineaire) Lorentz transformatie is dus geen sprake.
Thermische expansie en contractie (onder invloed van energie, te meten als afstand per graad) is een eigenschap van het proces van opwarming ten opzichte van een referentie, gelijkaardig aan de verschuiving van frequentie onder invloed van snelheid (afstand per tijd). Beide zijn een relatieve expansie/contractie en dus een nieuwe verhouding.