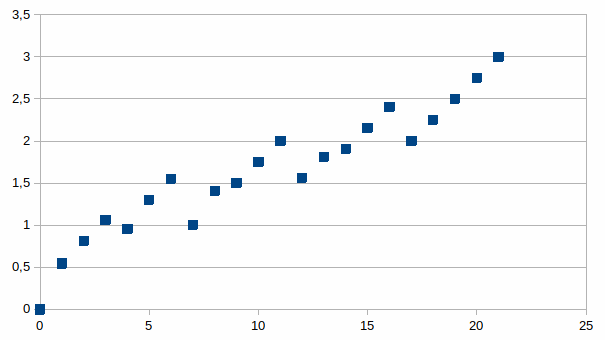De
entropie H(EDynamiek) is het getal -Σi(pi(log2pi))
waarbij pi de waarschijnlijkheid is dat een gebeurtenis
waargenomen wordt uit een dynamiek van gebeurtenissen die doorlopen
wordt door de entiteit E. De definitie van entropie wordt
gereconstrueerd en betekenis gegeven in het haakformalisme onder de
bijkomende voorwaarde van het doorlopen van (met andere woorden
ervaren van, of laten gebeuren van) elkaar uitsluitende
gebeurtenissen (zodanig dat een som van getallen verantwoord wordt)
in één en dezelfde potentiële tralie waarin atomen enkel kunnen
gebeuren, gebeurtenissen die elk staan voor een punt op een niveau in
een tralie waarbij elke gebeurtenis mogelijkerwijze door een aantal
AND-atomen gerealiseerd wordt. De constructie van het getal zorgt
ervoor dat de entropie maximaal is als alle gebeurtenissen even
waarschijnlijk zijn.
Het is belangrijk om nu in te zien dat die AND-atomen enkel kunnen
gebeuren en niet moeten kunnen gekozen worden, vandaar dat het zinvol
is om van een globale waarschijnlijkheid te spreken en niet alleen
van een voorwaardelijke waarschijnlijkheid (want
er gebeurt ook altijd iets anders dan wat we kunnen kiezen,
onafhankelijk van wat we kiezen blijft dit gelden). Een AND-atoom dat
gebeurt veronderstelt onvermijdelijk (globaal, dus niet enkel
voorwaardelijk) een corresponderend OR-atoom dat gekozen wordt, dus
met zekerheid “ja” geeft. We willen nu precies bepalen wat de
maat “entropie” als zekerheid kan meten.
We geven hiervan een eenvoudig voorbeeld met vier elkaar
uitsluitende punten. In het speciale geval dat er maar vier
toestanden zijn is de waarschijnlijkheid van het onvermijdelijk
ervaren van één AND-atoom ¼. Dit is in de potentiële tralie. Neem
nu het punt van het ander atoom niveau (het OR-atoom) dat
onvermijdelijk ervaren is. Op dat niveau wordt elk punt gerealiseerd
door drie atomen. Wanneer we nu één van de vier OR-atomen kiezen om
te ervaren, stel ab, dan is de waarschijnlijkheid van realisatie drie
maal “ja” en een maal “neen”. Zowel “ja” als “neen”
zijn relevant voor een waarneming. We gaan dus over naar de
tralie van relevantie, de tralie waarin “relevant zijn” de
relatie is die overeenkomt met “ervaren zijn” in de potentiële
tralie. Dus “ja” betekent in deze tralie “is relevant” maar
ook “neen” betekent evenzeer “is relevant”. Dat wat niet
relevant is wordt dus niet eens opgemerkt en stellen we voor als de
al-nul vector. We zullen de vier toestanden in de potentiële tralie
dus afbeelden op vier toestanden in
een tralie van relevantie in twee onderscheidingen. We
veronderstellen dus vier waarschijnlijkheden die we relateren met de
vier atomen, p[a]×[b], pa×[b], p[a]×b,
pa×b. De entropie H is dus het getal
H=-p[a]×[b](log2p[a]×[b])-pa×[b](log2pa×[b])-pp[a]×b
(log2pp[a]×b )-pa×b(log2pa×b).
Dus: als toestand [a]×[b] relevant is (ondanks het feit dat dit
punt niet kon gekozen worden, het is de onvermijdelijke relevantie in
een dynamiek), binair geldt dus (xxx.), dan is ook toestand a×b
relevant, dus binair is dat (x...). Ook als toestand [a]×b relevant
is, binair geldt dus (x.xx), dan is ook toestand a×b relevant,
binair is dat (x...), als toestand a×[b] relevant is, binair geldt
dus (xx.x), dan is ook toestand a×b relevant, binair is dat (x…).
Maar dat geldt niet voor toestand a×b. De relevantie van a×b staat
daar los van en moet afzonderlijk in rekening gebracht worden langs
de binaire representatie (.xxx).
We berekenen nu de entropie -Σi(pi(log2pi))
op elk niveau.
Het punt <> is ervaren met waarschijnlijkheid 1, zekerheid
dus met minimale entropie. Het punt <<>> is ervaren met
waarschijnlijkheid 0, zekerheid dus met evenzeer minimale entropie.
De minimale entropie is zeker niet nul, log2(0) is niet
gedefinieerd, we kiezen dus voor de betekende (….) als supremum en
vullen het als volgt in: de entropie op het niveau van de AND-atomen
of OR-atomen in de potentiële tralie heeft vier componenten in de
som met waarschijnlijkheid ¼ en is dus 4(-1/4log2(1/4))
of dus 2log2(2). We blijven log2(2) schrijven
omdat dit de eenheid is die we niet willen verdoezelen en die hier
intensiteit 2 krijgt (log2(2)+log2(2)=2log2(2)).
Die intensiteit geeft dus de grootte van het universum. Bij 1
onderscheiding is de intensiteit 1, bij 3 onderscheidingen is de
intensiteit 3, bij n onderscheidingen is de intensiteit n.
We gaan nu over van de potentiële tralie naar de tralie van
relevantie: het “ja-neen” onderscheid van de potentiële tralie
wordt afgebeeld op “relevant” in de tralie van relevantie zodanig
dat de nul vector (die niet voorgesteld wordt in de potentiële
tralie) afgebeeld wordt op “niet relevant” in de tralie van
relevantie. De entropie van dat extremum (de al-nul vector) in de
tralie van relevantie kan niet gemeten worden want log2(0)
is niet gedefinieerd, en kan enkel berekend worden op het atoomniveau
van de potentiële tralie, het niveau dat het mogelijk maakt om te
tellen (AND-atomen sluiten elkaar uit dus XOR is niet verschillend
van OR en duaal: OR-atomen sluiten elkaar in, dus XNOR is niet
verschillend van AND). De potentiële tralie is altijd een hypothese,
heeft een intensiteit (bijvoorbeeld een aantal atomen) die we enkel
kunnen veronderstellen.
De entropie op het niveau van de OR-atomen in de tralie van
relevantie heeft maar twee componenten in de som, een met
waarschijnlijkheid ¾ want elk van de vier OR-atomen worden
gerealiseerd door telkens drie AND-atomen (met dezelfde
waarschijnlijkheid, ¼+¼+¼= ¾) en één met waarschijnlijkheid ¼.
De som is dus -3/4log2(3/4)-1/4log2(1/4). Dit
is
-3/4log2(3)+3/4log2(4)+1/4log2(4)=4/4log2(4)-3/4log2(3)=2log2(2)-3/4log2(3).
Om expliciet de eenheid te tonen schrijven we dit nu als
(2-3log2(3)/4log2(2))log2(2). Als we
vergelijken met het AND-atoom niveau in de potentiële tralie is de
intensiteit van de entropie dus afgenomen met 3log2(3)/4log2(2)
of dus 1.1887218755408672. Het entropieverschil ΔH is positief. Dit
geldt voor elk punt op OR-atoom niveau in twee onderscheidingen.
Op centraal niveau in de tralie van relevantie is de som van de
twee componenten dan -2/4log2(2/4)-2/4log2(2/4)=+4/4log2(2)
en dat is 2log2(2)-log2(2). Als we vergelijken
met het AND-atoom niveau in de potentiële tralie is de entropie dus
afgenomen met log2(2) of dus 1. Dit is dezelfde entropie
voor de zes punten op centraal niveau.
De entropie op het niveau van de AND-atomen in de tralie van
relevantie is exact dezelfde als de entropie op het niveau van de
OR-atomen in de tralie van relevantie door de symmetrie in de tralie.
Als we vergelijken met het AND-atoom niveau in de potentiële tralie
is de entropie dus afgenomen met 3log2(3)/4log2(2)
of dus 1.1887218755408672.
Dit laatste is een belangrijke vaststelling en dit is het gevolg
van de constructie van het getal entropie. De entropie die we hier
berekenen zal minimaal twee termen in de som hebben, en zal altijd
tot twee termen kunnen teruggebracht worden, hoe groot het universum
ook zou zijn. Dit is het gevolg van de enige twee waarden die
relevant kunnen zijn. Om dit te onderscheiden van andere getallen die
“entropie” genoemd worden, kunnen we deze entropie een “relevante
entropie” noemen. Voor de extrema is de “relevante entropie”
niet gedefinieerd (minstens één van de twee termen is dan gelijk
aan nul) en het is die “relevante entropie”, los van de waarde
van de extrema, die de structuur van de tralie reflecteert. Het
benoemen van de eenheid log2(2) is dus essentieel en legt
het verband met de veronderstelde potentiële tralie en het aantal
onderscheidingen.
Gevolgen
De grootste “relevante entropie” zullen we altijd vinden op
het centraal niveau van de tralie van relevantie, het niveau waar er
evenveel betekende als onbetekende bits te vinden zijn. Onafhankelijk
van de grootte van het universum zal deze entropie gelijk zijn aan 1
en de entropie van alle andere niveaus zal groter zijn dan nul en
kleiner dan 1. ΔH zal altijd het verschil zijn van twee positieve
getallen. Een “relevante entropie” gelijk aan nul is onbereikbaar
en gewoon het gevolg van de manier waarop “de relevante entropie”
gedefinieerd werd.
Hieronder het verloop van “de relevante entropie” H voor de 15
niveau’s tussen de suprema van een universum met vier
onderscheidingen, de suprema zijn dus onbereikbaar. We hebben een
kwadratische trendlijn en een vierde macht trendlijn weergegeven met
hun determinatiecoëfficiënt.
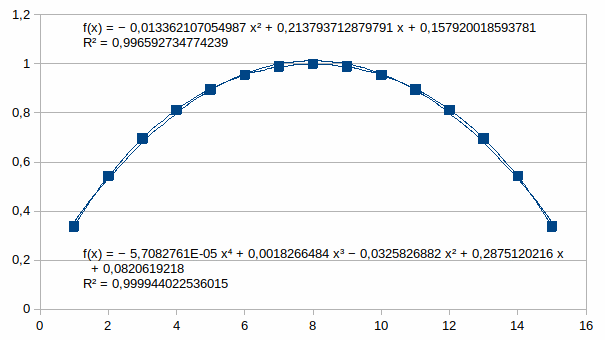
De
extrema worden dus niet voorgesteld, de nul wordt dichter benaderd in
een groter universum en dat kan een willekeurig dichte benadering
zijn waarmee we de veronderstelling van het potentieel universum
modelleren. Hieronder een deel van de grafiek voor 7 onderscheidingen
en trendlijnen als veeltermen uitgedrukt in achtste en vierde macht.
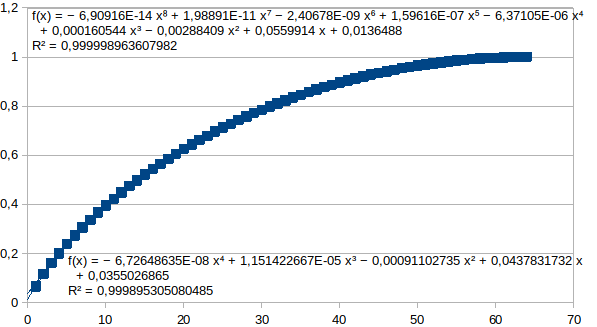
Uiteindelijk zijn sommige punten van deze curven identiek, de
curven onderscheiden zich doordat er meer of minder punten tussen
identieke punten getoond worden. Inderdaad: pi(log2pi)
voor vier toestanden genereert twee soorten van twee verschillende
punten: enerzijds <<3/4log2(3/4) en 1/4log2(1/4)>>
en anderzijds <<2/4log2(2/4) en 2/4log2(2/4)>>
en beide vinden we terug in hogere universa, bijvoorbeeld in vier
onderscheidingen zijn deze enerzijds <<12/16log2(12/16)
en 4/16log2(4/16)>> en anderzijds <<8/16log2(8/16)
en 8/16log2(8/16)>>. Dat geldt voor alle punten,
bijvoorbeeld het punt dat overeenkomt met 1/8 of 3/8 is niet terug te
vinden in twee onderscheidingen, maar wel in vier onderscheidingen
als 2/16 en 6/16. Dat kunnen we modelleren door het verloop van de
entropie als een veelterm van een hogere graad te berekenen (de
exponent van de hoogste macht van x waarvan de coëfficiënt
verschillend is van nul).
Dit maakt heel duidelijk hoe “de relevante entropie” gebaseerd
is op een onderscheidingen universum. Dit kan dan bijvoorbeeld de
“Gibbs
paradox” of de “mengeling paradox van identieke gasmengsel”
verklaren met de interpretatie van entropie die in de statistische
mechanica gebruikt wordt: of we een paradox vinden of niet hangt
samen met het kunnen onderscheiden van individuele atomen
(Gibbs) of van het kunnen onderscheiden van twee “identieke”
gassen (in een mengeling) en hangt dus af van de relevante
onderscheidingen, niet van de atomen of gassen als zodanig.
Zoals het niveauverschil een metrische maat is in twee dimensies,
is ook de “relevante entropie” een metrische maat in twee
dimensies: de niveaus van de tralie als een eerste dimensie en een
getal tussen 0 en 1 als de tweede dimensie. De twee termen van de
“relevante entropie” zijn gebaseerd op 1/n en (1-1/n). Dit
herkennen we natuurlijk als complementaire waarschijnlijkheden of als
de waarschijnlijkheid van twee maal dezelfde uitkomst in een discrete
partitie (namelijk 1/n2 versus n(n-1)/n2 zoals
gemodelleerd door David Ellerman).
Dat is niet anders dan dezelfde soort vrijheid die we hebben om
een aantal bits n en een aantal gemeenschappelijke bits m te kiezen
bij de
constructie van een kandidaat tralie die minstens twee punten kan
representeren.
Van relevantie afgeleide soorten entropie
We geven twee voorbeelden van berekening van een entropie op basis
van een selectie van relevantie. Ze zijn exemplarisch voor de soorten
entropie die in werkelijkheid zouden kunnen gebruikt worden.
Venn diagram
De veronderstelling die we maakten om entropie te modelleren (de
tralie van relevantie) zijn exact de veronderstellingen die we ook
nodig hebben om Venn-diagrammen
te modelleren. Voorgesteld in zo’n diagrammen zijn de getallen dus
niet anders dan de oppervlakte van (sommen van) gebieden in die
diagrammen, gebaseerd dus op een berekening met een logisch
criterium. Maar dat betekent dus ook dat deze sommen op veel
verschillende manieren kunnen berekend worden en sommige van deze
manieren zullen perfect op minder onderscheidingen af te beelden zijn
dan het aantal onderscheidingen dat nodig is om het totaal aantal
toestanden in het grootste universum te kunnen modelleren.
Alle deelverzamelingen in onderstaand model zijn door sommen te
construeren aangezien de 7 AND-atomen elkaar uitsluiten.
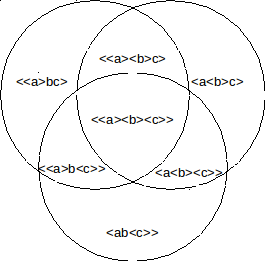
Een
bepaalde verdeling van oppervlaktes leidt dan tot een entropie
-Σi(pi(log2pi)) met i in
dit geval gelijk aan 7, entropie die maximaal zal zijn als alle
oppervlaktes identiek zijn (bijvoorbeeld 1/7). De entropie
verschillen zullen evoluties modelleren die slechts door 7 van de 8
toestanden gerealiseerd worden. De achtste toestand is a priori
ervaren en dus persistent. Dezelfde modellering is misschien ook in
grotere universa mogelijk, maar dat is zeker geen klassiek continuüm
waarin een monotone toename of afname te vinden is.
Young diagram (partities)
In plaats van te vertrekken van onderscheidingen kunnen we ook
vertrekken van een aantal toestanden. Het aantal toestanden is een
geheel getal en elk geheel getal kan geschreven worden als een som
van partities en de partities kunnen
we interpreteren als een soort. Bijvoorbeeld voor het getal 4
zijn de volgende sommen mogelijk: 4 en dus één soort; 3+1, 2+2 en
dus twee soorten; 2+1+1 en dus drie soorten; 1+1+1+1 en dus vier
soorten. In totaal heeft 4 dus 5 partities. Voor 5 zijn de volgende
sommen mogelijk: 5 en dus één soort; 4+1, 3+2 en dus twee soorten;
3+1+1, 2+2+1 en dus drie soorten; 2+1+1+1 en dus vier soorten en
1+1+1+1+1 of vijf soorten. Hiermee hebben we de 7 partities van 5
geïnterpreteerd.
Een praktische toepassing van deze opsplitsing in soorten (in maar
twee soorten in dit geval) is de manier waarop we een deeltralie
onderscheiden hebben van
een meetcontext met “p3 versus <p2>” als “M versus
M<>” en waarin 10100000 de rol inneemt van de
M•M<>↔MM<>. Dit is trouwens ook
het model dat we gebruikt hebben om de
stelling van Bayes in de waarschijnlijkheidsrekening te
illustreren.
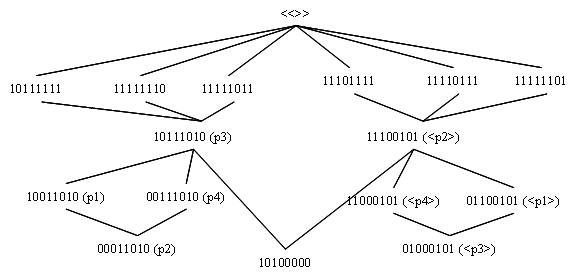
We hebben dat dan uitgebreid met andere soorten waarmee we het
verschil tussen kwantum en klassiek konden illustreren.
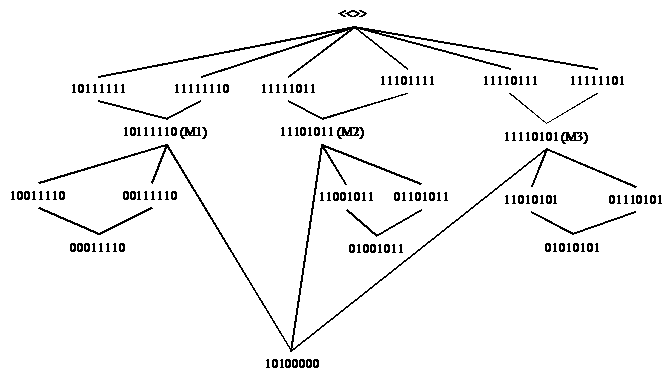
Soorten hebben we dan ook meer abstract voorgesteld als
gelijkwaardige bitstrings, gelijkwaardige
eenheden. Sommige soorten sluiten elkaar uit en dus zijn ook
telbaar. Veronderstel 5 toestanden in vier soorten, dan wordt de
relevante entropie
(2/5)log2(2/5)+(1/5)log2(1/5)+(1/5)log2(1/5)+(1/5)log2(1/5).
Voor 10 toestanden in vier soorten zouden we vier verschillende
getallen bekomen als volgt:
(4/10)log2(4/10)+(3/10)log2(3/10)+(2/10)log2(2/10)+(1/10)log2(1/10)
want 10=4+3+2+1.
Een eenvoudig voorbeeld van een veranderende partitie is de
interactie van een chemisch element (soort 1) met een
oplossingsmiddel, bijvoorbeeld een zuur in water. De interactie is
dat het element dissocieert in een positief ion (soort 2) en een
negatief ion (soort 3), waarbij het aantal entiteiten in oplossing
verdubbelt als alle elementen van soort 1 zouden getransformeerd zijn
naar de twee andere soorten. De verandering gebeurt afhankelijk van
de omgeving dat het chemische potentiaalverschil bepaalt (een energie
per mol of per deeltje die beschikbaar wordt of die vrijkomt) dat het
spontaan proces mogelijk maakt. Andere onderscheidingen (typisch zijn
dat de temperatuur en druk) zullen bepalen welke aantallen van welke
soort met elkaar in evenwicht zijn (en dan een hoeveelheid energie
bufferen). De verandering van partities is het (waarneembare) spoor
dat achtergelaten wordt door de actie van de beschikbare energie die
naar een andere vorm omgezet kan worden in een proces waarin we
onvermijdelijk een aantal stappen kunnen onderscheiden. Die stappen
kwantificeren het aantal toestanden met een vermogen dat nog kan
veranderen (dit noemen we de exergie of vrije energie). Wanneer de
energie gelijkmatig verdeeld is over de mogelijke partities is er
geen vermogen meer beschikbaar en dat drukken we uit door een
geconstrueerd getal, de entropie, een maximum te laten bereiken.
De toename van entropie reflecteert het aantal soorten maar het
verband is niet lineair. Hieronder een grafiek van de entropie voor
de 22 partities van 8 toestanden. We kiezen voor 8 toestanden omdat
dit het aantal is in een universum van drie onderscheidingen. Het is
duidelijk dat de entropie niet monotoon toeneemt. We merken een
aantal “fase overgangen” die het gevolg zijn van het aantal
soorten toestanden die onderscheiden worden. Binnen één fase neemt
de entropie monotoon toe en elke fase start met de entropie van de
partitie met kleinste aantal. Entropie verschillen zijn belangrijker
dan entropie waarden (zoals energieverschillen belangrijker zijn dan
energiewaarden, of vermogen verschillen belangrijker zijn dan de
waarden van de vermogens). Zoals steeds is evenwicht te modelleren
als een som van verschillen die niet meer te onderscheiden zijn.
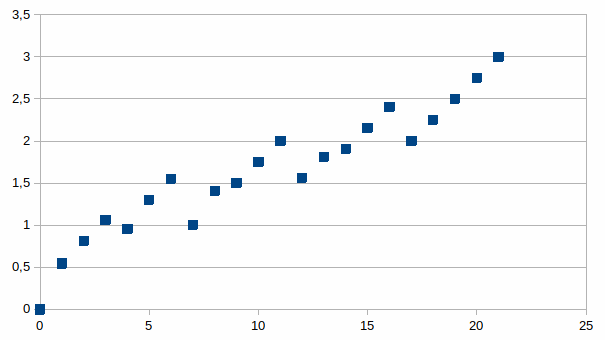
De reeks bij het hoogste aantal partities wordt altijd gevormd
door het aantal soorten met “een of twee” (disjunctie)
toestanden, deze reeks neemt lineair toe en culmineert wanneer het
aantal even waarschijnlijke toestanden bereikt wordt die elk als een
soort beschouwd worden. In de grafiek is dat het punt met waarde
3=log2(8).
Deze grafiek laat zien dat de entropie toeneemt, maar enkel
monotoon toeneemt voor de evolutie binnen één fase. De fase eindigt
met een “reorganisatie” van de verdeling van toestanden met
laagste entropie en een nieuwe fase begint die dan uiteindelijk de
entropie nog verder kan laten toenemen. Dit gaat door tot alle
toestanden gelijkmatig over de soorten verdeeld zijn, een typisch
voorbeeld is een thermisch evenwicht. Thermisch evenwicht is de
situatie waarin het zinvol is om van een “gemiddelde temperatuur”
en dus een gemiddelde energiedensiteit te spreken. Energiedensiteit
is vermogen en dus processnelheid, energiedensiteit is energie per
vrijheidsgraad, energiedensiteit is energie per temperatuurstap.
Energiedensiteit (vermogen) is exergiedensiteit omdat enkel wanneer
er nog vrije energie is die getransformeerd wordt (een
vermogen densiteit), energie kan waargenomen worden. De situatie
van evenwicht is er een van maximale entropie, er is dan geen
vermogen meer waarneembaar. Wanneer de hypothese is dat energie niet
kan verdwijnen en niet uit het niets kan ontstaan, dan “moet er wel
nog <<iets>> zijn als <<het>> niet
waargenomen kan worden” en dat moet dan die energie zijn. De
spontane evolutie is er een van ver-van-evenwicht naar evenwicht. Het
entropieverschil is steeds positief en is functie van het maximum
aantal van de soorten die onderscheiden kunnen worden. Het maximaal
aantal niveauverschillen in de beschrijvende tralie bepaalt hoe klein
het entropieverschil kan worden. Hieronder de fasen uit de grafiek in
een tabel om aan te geven hoe ze verdeeld zijn over de verschillende
niveaus (aangegeven tussen haken) en dat voor de 22 partities in drie
onderscheidingen. Er zijn altijd n-1 fasen met n het aantal
toestanden. Fase 6 en fase 7 kunnen eigenlijk niet onderscheiden
worden (ze zijn deel van hetzelfde lineair verloop).
Fase
0 (8)
|
Fase
1 (7)
|
Fase
2 (6)
|
Fase
3 (5)
|
Fase
4 (4)
|
Fase
5 (3)
|
Fase
6 (2)
|
Fase
7 (1)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
0
|
0,54
|
0,81
|
1,06
|
0,95
|
1,3
|
1,55
|
1
|
1,41
|
1,5
|
1,75
|
2
|
1,56
|
1,81
|
1,91
|
2,16
|
2,41
|
2
|
2,25
|
2,5
|
2,75
|
3
|
Stel dat men zou willen dat fase 5 stabiel blijft (en dus de
entiteit met laagste entropie op niveau 3 in de tralie invariant kan
blijven), dan moeten we kunnen onderzoeken of andere fasen kunnen
gebruikt worden als deelprocessen in de omgeving van de entiteit op
niveau 3 die de nodige entropie produceren om stabiliteit mogelijk te
maken voor de entiteit in fase 5. De omgeving van de entiteit op
niveau 3 is niet anders dan “iets anders dan de entiteit op niveau
3”, en voor elke welgevormde haakuitdrukking is dat een goed
gedefinieerd begrip. Evenwicht
is te modelleren door een som van verschillen, som die willekeurig
klein en onwaarneembaar kleiner kan gemaakt worden. Vanuit de
hypothese dat energie niet kan verdwijnen en niet uit het niets kan
ontstaan moeten we wel een proces kunnen vinden dat in de totale
werkelijkheid ervoor kan zorgen dat de entiteit op niveau 3 kan
blijven bestaan. Dat zien we bijvoorbeeld als we een nieuwe molecule
synthetiseren in een reactievat met oplosmiddel, een proces dat (een
deel van) de thermische energie in het oplosmiddel hiervoor als
persistent chemisch potentiaal in een specifieke molecule vastlegt.
Dit kan trouwens de complexiteit verklaren van (levende) systemen.
Hieronder de grafiek voor de entropie van de 231 partities van 16
toestanden.
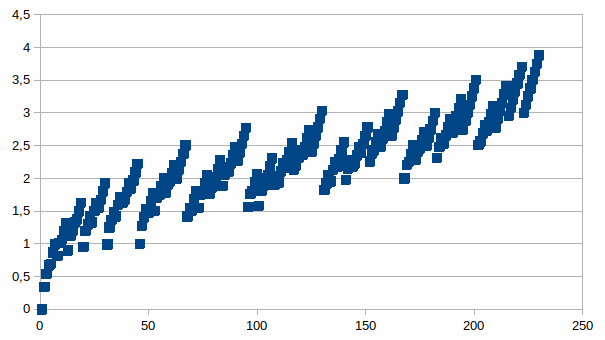
Het aantal partities van n (en dus het aantal soorten die zouden
kunnen gebruikt worden om n toestanden te onderscheiden als
onderscheid tussen soorten maar niet tussen elkaar) zijn te vinden op
OEIS.
De partities vormen een tralie. Dit wordt de tralie van Young
genoemd met als elementen “Young diagrammen”, mogelijke
configuraties van eenheidsblokjes. Deze tralie vertoont symmetrieën,
zo ziet men onmiddellijk in elk niveau van de tralie duale diagrammen
(dezelfde aantallen per rij voor de ene, per kolom voor de andere) en
centraal op elk niveau een zelfduaal diagram. Hieronder de tralie
voor de partities tot en met het getal 6. De verbindende lijnen geven
de partiële orde weer: 1 blokje wordt toegevoegd of weggelaten
tussen elementen van aanliggende niveaus.
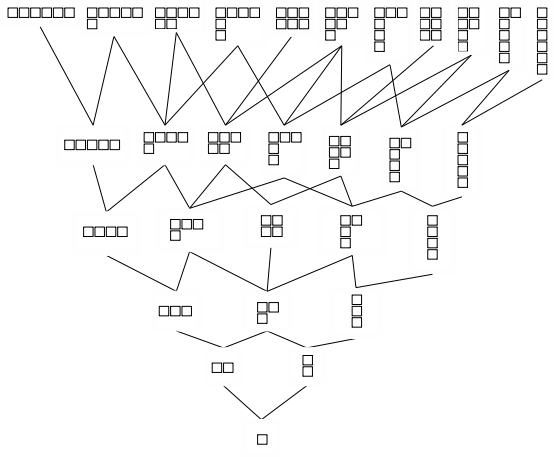
De tralie van Young geeft een visueel beeld van de invariantie van
sommige soorten als volgt: neem het blok van 2x2 toestanden dat voor
het eerst ontstaat als mogelijkheid met vier toestanden. Dat blok
blijft herkenbaar, 2 maal in vijf toestanden en 7 maal in zes
toestanden.