Een disjunctie van welgevormde haakuitdrukkingen die we als nieuwe eenheid gebruiken drukt uit dat die haakuitdrukkingen als gelijkwaardig beschouwd worden. We laten nu expliciet zien dat dit gekwantificeerd kan worden door een niveau verschil in een tralie, maar eens we een tralie betreden moeten we een duidelijk onderscheid maken tussen intensiteit en eenheid.

We illustreren dit met de volgende tralie:

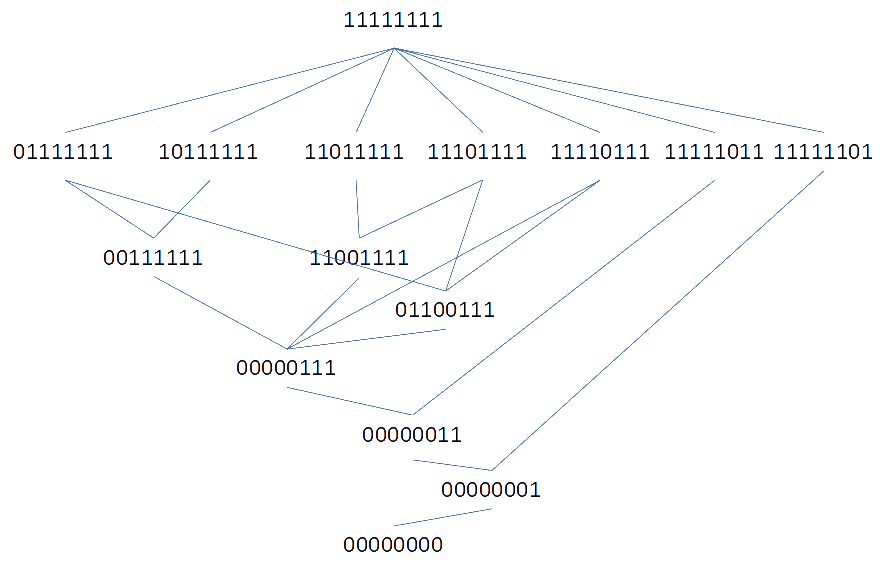
We tellen de niveaus vanaf het bovenste extremum. Er zijn zeven punten op niveau 1 (dat is een intensiteit 7 van punten van dezelfde soort), zij zijn allemaal gelijkwaardig voor de eenheid (00000001), infimum van deze zeven punten. We kunnen deze laatste eenheid dus voorstellen als (0⁷1¹), waarbij we de intensiteit van de laagbit en hoogbit in de exponent weergeven. Deze notering maakt duidelijk dat we nu enkel naar het aantal laagbits en het aantal hoogbits kijken, niet naar hun positie. Dus alle bitstrings op hetzelfde niveau zijn equivalent, spelen dezelfde rol, hebben dezelfde voorstellingskracht.

Twee punten op niveau 1, namelijk (01111111) en (00111111), zijn gelijkwaardig voor eenheid (00111111) dat hun infimum is en zich op niveau 2 bevindt. Twee andere punten op niveau 1 zijn gelijkwaardig voor eenheid (11001111) die zich eveneens op niveau 2 bevindt en beide nieuwe eenheden zouden gelijkwaardig zijn voor een eenheid (00001111) op niveau 4, maar deze eenheid is niet beschikbaar in de tralie. Als we dat in exponenten zouden voorstellen, stellen we zowel (00111111) als (11001111) voor als (0²1⁶) en (00001111) stellen we voor als (0⁴1⁴). De intensiteit van bits is dus gegeven door de exponent.

In de tralie is (00000111) wel voorgesteld, een eenheid op niveau 5, infimum van 5 punten op niveau 1. Als we dat in exponenten voorstellen, stellen we (00000111) voor als (0⁵1³). We stellen zowel (00111111) als (11001111) voor als (0²1⁶) en dat zijn twee eenheden op niveau 2 die gelijkwaardig zijn met een eenheid op niveau 1, namelijk (11110111). Gelijkwaardigheid van bitstrings op verschillende niveaus is dus mogelijk. (0²1⁶) en (0⁷1¹) kunnen gelijkwaardig zijn als hun infimum beschikbaar is in de tralie.

Er is een eenheid op niveau 3 voorgesteld, namelijk (01100111). Deze eenheid drukt uit dat (01111111) op niveau 1 niet alleen een soort gelijkwaardigheid heeft met (10111111) maar een andere soort gelijkwaardigheid met andere punten op niveau 1, namelijk (11101111) en (11110111). Er zijn dus meerdere soorten gelijkwaardigheid die we niet zomaar kunnen optellen zonder rekening te houden met de structuur in de eenheden. Dus wanneer we (01100111) als (0³1⁵) voorstellen dan impliceert dat in deze tralie dat we andere eenheden moeten samentellen, eenheden die van een ander niveau zijn.

We illustreren dat met de relevante deeltralie: het punt (01100111) op niveau 3 kan wel met de punten (10111111), (11011111) en (11111011) op niveau 1 opgeteld worden ten opzichte van infimum (00000011) op niveau 6. Het is duidelijk dat dit het gevolg is van het feit dat de vier punten: (01100111), (10111111), (11011111) en (11111011) elkaar uitsluiten ten opzichte van hun infimum (00000011). Voor dat infimum zijn de vier punten gelijkwaardig.

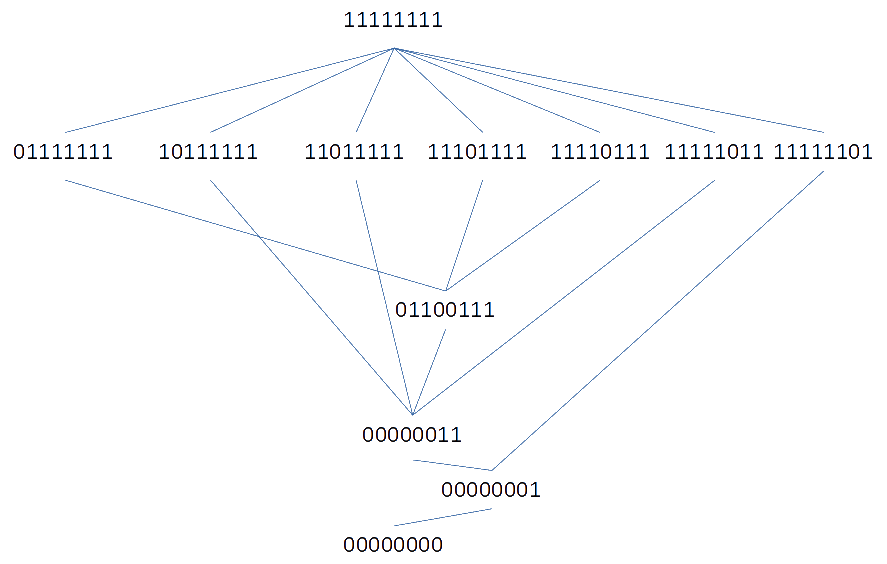
Dit maakt ook duidelijk dat we verschillende partities kunnen beschouwen van het maximum aantal bits, maar dat niet alle partities a priori als gelijkwaardig kunnen beschouwd worden, iets waar we rekening moeten mee houden als we tellen.

We kunnen nu ook nog een stap verder gaan door alle punten van een volledige tralie T als gelijkwaardig te beschouwen, wat zich dan ook zal manifesteren als de intensiteit van een bit van een nog langere bitstring dan de bitstrings die de tralie T opspannen, en die misschien maar gedeeltelijk gekend kan worden. Dit kunnen we inderdaad aantonen met voorbeelden uit het getallendomein waarbij we de gevolgen kunnen onderzoeken (elke eenheid moet zijn eigen schaal krijgen, wat onder andere betekenis geeft aan afgeleiden).