We hebben gezien dat een getal beschouwd kan worden als de realisatie van een telbare relatie tussen variabelen (variabelen die dus beschouwd worden als entiteiten). De intensiteit van de individuele variabelen in het getallendomein hebben de ordening van de gehele getallen. Dit is de ordening van de som van getallen en dit is hoe we getallen in werkelijkheid gebruiken als telling (3x1 is de korte notering van de som x1+x1+x1).
Stel dat we een telbare uitdrukking poneren in drie variabelen: x12 + x2 + x3. Het verbindend plusteken is de plus van het getallendomein zowel als de plus tussen entiteiten die elkaar uitsluiten (dit zijn in dit geval de drie variabelen) zoals we ook toestanden met elkaar kunnen sommeren. Dit is dus een voorbeeld van een welgevormde uitdrukking in het getallendomein die nog geen waarde toegekend gekregen heeft. Dat betekent dus concreet dat er nog niet vastgelegd werd welk(e) getal(len) door de relatie van product en som tussen drie variabelen voorgesteld wordt (of hoe x12 + x2 + x3 als de definitie van een getal kan gebruikt worden). Dit is volledig analoog als de manier waarop een welgevormde haakuitdrukking, die nog geen waarde toegekend gekregen heeft, voorgesteld wordt met product en som die voor haakvectoren gedefinieerd werd. We noemen deze welgevormde uitdrukking t1. Hiermee introduceren we niet alleen een nieuwe variabele maar als welgevormde uitdrukking in het getallen domein beschouwen we t1 als een transformatie van maximaal drie variabelen die één getalwaarde kunnen krijgen. We poneren nu ook een andere entiteit: x12 + 2x2 + 3. We noemen deze t2. Als welgevormde haakuitdrukking in het getallen domein beschouwen we deze uitdrukking als een transformatie van maximaal twee variabelen die ook in de eerste uitdrukking voorkomen. We veronderstellen nu dat beide transformaties evenwaardig zijn (dezelfde getalwaarde genereren) ondanks het feit dat we de waarde niet kennen, formeel moet dus gelden:
x12 + 2x2 + 3 ↔ x12 + x2 + x3
of t1 ↔ t2
Deze uitdrukking is dus weer een transformatie en de transformatie kunnen we dus realiseren (een waarde toekennen) door de vergelijking x12 + 2x2 + 3 = x12 + x2 + x3 te reduceren, wat resulteert in x2 + 3 = x3, of dus de volgende "indien... dan..." constructie voor het getal 3:
3 = x3 - x2
Dit betekent dus dat de vijf variabelen die geïntroduceerd werden (namelijk x1, x2, x3, t1, t2) gereduceerd worden tot twee variabelen (namelijk x2 en x3). Het is daarbij ook duidelijk dat we altijd variabelen kunnen toevoegen, maar dat het niet altijd mogelijk zal zijn om sommige variabelen weg te laten. De opgespannen tralie in vijf variabelen is nu naar een gecollapste vorm gereduceerd, volledig analoog als de collaps van bijvoorbeeld <> ↔ a•b, die het hele twee onderscheidingen universum collapst naar de deeltralie waarin a•b niet kan onderscheiden worden van de waarde <>. Het proces dat hieronder verscholen ligt kunnen we nu verduidelijken: in het haakformalisme waarin er maar één waarde is, is duidelijk dat 3 = x3 - x2 beter geschreven wordt als 1 = 3-1 (x3 - x2). Dit betekent dat we beide termen van de vergelijking vermenigvuldigen met de factor 3-1. Volledig gelijkaardig zouden we beide termen kunnen vermenigvuldigen met de factor (x3 - x2)-1 en schrijven: 3(x3 – x2)-1 = 1.
Nu gebruiken we de analogie waarin we in het haakformalisme van <<>>•<<>>↔<<>>•b kunnen overgaan op a ↔ a•b (omdat de dubbele pijl en de dot-notatie dezelfde bewerking uitvoeren en het haakformalisme dus een positieve constructiemethode mogelijk maakt). Dus: een “oplossing zoeken” voor t1 ↔ t2 betekent dat we op zoek gaan naar een transformatie t3 zodanig dat
t3 * t1 ↔ t3 * t2
We gebruiken hier voor het product de notatie * omdat blijkt in het getallendomein dat transformaties gericht zijn. Hiermee drukken we het volgende uit: het grote verschil met de aspecten die relaties coderen in haaknotatie is dat in het getallendomein de entiteiten elkaar uitsluiten, dit betekent dat er een ordening, een geordend interval, in het getallendomein een rol speelt en de ordening is anders voor de getallen vergeleken met de reciproque getallen. Dit betekent, met het voorbeeld van t3 * t1, dat eerst de waardetoekenning uitgevoerd wordt voor t1 en daarna voor t3 (we gebruiken hier de meest gevolgde conventie voor de orde van functie en argument).
We kunnen nu een aantal transformatie bedenken die voldoen aan t3 * t1 ↔ t3 * t2. We geven als voorbeeld van transformatie t3 de volgende stelsels die we hun eigen transformatie naam geven:
t4 |
t5 |
t6 |
t7 |
x1 ↔ 1 x2 ↔ -1 x3 ↔ 2 |
x1 ↔ -5 x2 ↔ y1 -1 x3 ↔ y1+2 |
x1 ↔ y1 x2 ↔ y2 x3 ↔ y2+3 |
x1 ↔ 1 x2 ↔ x2 x3 ↔ x2+3 y3 ↔ x1 +x2 |
Elk stelsel is een conjunctie van waardetoekenningen aan variabelen. Terwijl men oplossingen bedenkt zoals hier in de tabel, wordt duidelijk dat die oplossingen op een of andere manier met elkaar verbonden zijn. We merken bijvoorbeeld dat er voor sommige oplossingen andere constanten optreden en dat er meerdere variabelen kunnen toegevoegd worden, en dat het op die manier duidelijk wordt dat het uitbreiden van onderscheiden elementen in een taal aanleiding kan geven tot meer algemene oplossingen, maar dat men daarin ook kan overdrijven (bijvoorbeeld: hebben we y3 echt nodig om een verschil te maken dat een verschil maakt?). Er zal een optimum kunnen gedefinieerd worden. De meest algemene oplossing is de oplossing die het meest onafhankelijk is van een gekozen waardetoekenning. Dit is te herkennen omdat alle andere oplossingen met waardetoekenningen een realisatie kunnen zijn van de meest algemene oplossing. Juist dit is een voorbeeld van simultaneïteit, en we begrijpen dus dat transformaties in het getallendomein gericht zijn.
We merken dan het volgende op: elke conjunctie (logische AND) is niet alleen simultaan met een transformatie (logische XNOR) maar kan daar ook niet van onderscheiden worden omdat alle getallen elkaar uitsluiten. We kunnen nu berekenen dat t6 algemener is dan de andere transformaties. Bijvoorbeeld: t6 is fijner dan t5 omdat er een t8 gevonden wordt waarbij de volgende relatie geldt:
t5 ↔ t8*t6
Deze t8 is immers de conjunctie van
y1 ↔ -5
y2 ↔ y1-1
Het begrip "meer algemene transformatie" heeft dus dezelfde betekenis als het begrip "fijnere haakuitdrukking".
Volledig analoog berekenen we
t4 ↔ t9*t6
Deze t9 is immers de AND van
y1 ↔ 1
y2 ↔ -1
en
t7 ↔ t10*t6
Deze t10 is immers de AND van
y1 ↔ 1
y2 ↔ x2
Conclusie: t6 is de meest algemene oplossing die het met de minste variabelen doet aangezien t4 en t5 en t7 als een samenstelling van transformaties met t6 kan gezien worden, en dat dit voor elke andere transformatie geldt die zich beperkt tot die variabelen. Hieruit volgt dat de welgevormde uitdrukking die door de collaps gedefinieerd werd in zijn meest algemene vorm kan voorgesteld worden als de uitdrukking in slechts twee variabelen: y12 + 2y2 + 3. Elke waardetoekenning in deze uitdrukking zal precies de waardetoekenning realiseren in de meer complexe uitdrukking met drie variabelen: x12 + 2x2 + 3 ↔ x12 + x2 + x3.
Elke veelterm is dus ook als stelsel te noteren door extra variabelen te introduceren, wat de “parameter representatie” genoemd wordt. Het omgekeerde, waarbij een of meerdere variabelen of parameters zouden moeten kunnen geëlimineerd worden, is niet altijd mogelijk. In het haakformalisme is dit gemakkelijk in te zien aangezien men gemakkelijk een onderscheiding kan toevoegen, maar niet alle punten van een meer-onderscheidingen universum op een minder-onderscheidingen universum één-op-één af te beelden zijn.
Het stelsel is het samen optreden van meerdere vergelijkingen, en is dus een logische conjunctie.
Zo is de parabool te schrijven als een logische conjunctie van twee namen die relaties van één parameter weergeven:
x=u
y=u2
In 1-splitsing notatie: (u, u2)
en een cirkel met straal s als een logische conjunctie van
x=s sin(u)
y=s cos(u)
De namen x en y zijn dan functies van één parameter: u.
Beide voorbeelden worden veralgemeend tot r(u)=(x(u), y(u)), staand voor een vector: de logische conjunctie van beide relaties, en dit is de voorstelling van een pad in twee dimensies met behulp van een één-dimensionale parameter die in staat is de intensiteit van de hogere dimensie(s) als de intensiteit van een bepaalde relatie te coderen.
Het volledig twee dimensionaal vlak wordt dan voorgesteld door de parametrische vergelijking r(u, v)=(x(u, v), y(u, v)), waarbij u en v als één-dimensionale parameters niet beperkt worden.
Dit kan onmiddellijk uitgebreid worden naar meerdere parameters zodanig dat een parametrische vergelijking een afbeelding zal zijn van een entiteit in i parameters naar een entiteit in j parameters {p1(t1, t2, ..., ti), p2(t1, t2, ..., ti), ..., pj(t1, t2, ..., ti)}.
Een speciaal geval is de afbeelding van een entiteit in i parameters naar de ene parameter t: {p1(t), p2(t), ..., pi(t)}, wat de beschreven entiteit kan modelleren als een logische conjunctie van variabelen pi en dat elke concrete realisatie van die logische conjunctie een andere concrete realisatie uitsluit (de definitie die aan “tijd” gegeven wordt). Een zeer illustratief voorbeeld zijn de lissajoux figuren
x=Asin(at+d)
y=Bsin(bt)
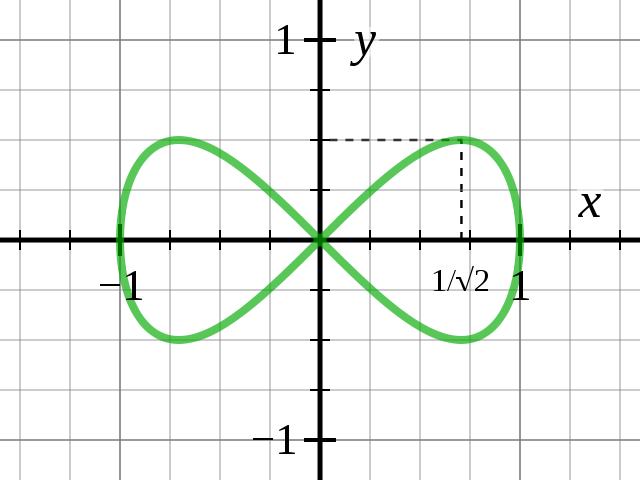
Met als voorbeeld de lemniscaat van Huygens (of Gerono) met als veelterm representatie x4-x2+y2=0 en enkele mogelijke parameter representaties:
x=cosφ
y=sinφ cosφ
of
x=cosφ
y=2-1sin2φ
of
x=(t2-1)(t2+1)-1
y=2t(t2-1)(t2+1)-2

Veeltermen drukken een potentiële relatie uit tussen variabelen die elkaar uitsluiten. Zij zijn dus een voorbeeld van welgevormde haakuitdrukkingen die elkaar uitsluiten. Een waardetoekenning aan een veelterm is de uitdrukking van een unieke transformatie. Tot en met drie variabelen kunnen we ons voorstellen dat de relatie een stabiele ruimtelijke vorm modelleert. Vanaf vier variabelen kunnen we met veeltermen ook dynamiek modelleren.