Spontane
processen zijn gesloten door de onmogelijkheid van, of het
vermijden van de interactie met andere processen (die dan de
buitenwereld genoemd worden). Dit drukt men uit door zo’n proces
zelforganiserend te noemen. De onmogelijkheid van interactie kunnen
we enkel maar aanvaarden. Het vermijden van interactie kunnen we
kiezen, vandaar dat men zegt dat (sommige) systeemgrenzen willekeurig
kunnen gekozen worden. Spontane processen beïnvloeden elkaar indien
er een koppeling bestaat die beide verandert, en dus per definitie de
grens van beide overschrijdt. Zelforganisatie kunnen we dus niet
alleen definiëren als spontane dynamiek
in één proces , maar kunnen we ook definiëren als de spontane
interactie van spontane processen, de spontane dynamiek
in meerdere processen waarin soms een invariant evenwicht kan
gevonden worden.
Zelforganisatie
Interactie is zelforganisatie wanneer we veronderstellen dat er
geen externe agens invloed uitoefent op het verloop van het proces
van interactie (wat een tautologie is en enkel in werkelijkheid kan
blijken). Zelforganisatie leidt tot gedrag dat autonoom genoemd
wordt, een ander woord om uit te drukken dat externe veranderingen
geen invloed uitoefenen op het bereiken van de attractor
van het proces. Soms leidt dit tot bestendiging van entiteiten, soms
leidt dit tot verdwijnen van entiteiten. Het proces kan immers ook
doorgaan zonder dat energie en materie geconserveerd worden, beide
worden door het proces in een andere vorm getransformeerd. Een proces
kan dus ook beschreven worden op het niveau van organisatie (de
relaties) van energie en materie en kan dus bestudeerd worden los
van de pakketjes materie en energie. Worden de entiteiten in het
proces bestendigd dan noemen we de entiteiten fit in hun omgeving (ze
beïnvloeden elkaar, passen zich aan aan elkaar en dus definiëren ze
elkaar). Verdwijnen de entiteiten dan zijn ze niet fit in hun
omgeving (de stabiliteit van de ene gaat ten koste van de stabiliteit
van de andere). Bijvoorbeeld: een multicellulaire entiteit
kan fit zijn terwijl een individuele cel als deelentiteit
van die multicellulaire entiteit dat niet is. Het leven als proces
van een multicellulaire entiteit vereist niet dat individuele cellen
moeten blijven leven.
Twee processen
Om de interactie van spontane processen te bestuderen
veronderstellen dus minimaal twee spontane processen. We
kunnen dit altijd aangezien er ook altijd iets anders gebeurt dan
waarop we gefocusseerd zijn. Dus indien we ons focusseren op één
spontaan proces dan nog kunnen we veronderstellen dat er simultaan
een ander spontaan proces doorgaat en we kunnen de hypothese
formuleren dat ze elkaar zouden beïnvloeden. Met twee voorbeelden
wordt dit duidelijk: gravitatie en elektromagnetisme zijn twee
spontane processen die elkaar wederzijds kunnen beïnvloeden.
Diffusie van een vloeistof door een medium is het samenspel van twee
spontane processen: het spontaan vloeien onder een potentiaal
verschil en de spontane verandering van het medium, beide processen
beïnvloeden elkaar.
Elk proces heeft zijn eigen spontaan tijdsverloop, wat betekent
dat elk proces door andere atomen (toestanden die elkaar onderling
uitsluiten) gekarakteriseerd kan worden. We kunnen beide processen
dus van elkaar onderscheiden, en dus uniek coderen, door de
toegevoegde vluchtige onderscheiding ℵ hiervoor te gebruiken,
het is immers die onderscheiding die niet ingebouwd wordt, die een
spoor kan zijn van het proces dat wel output maar geen input is. De
twee processen zullen we daarom het α-proces en het β-proces
noemen, waarbij het α-proces als vluchtige onderscheiding α heeft
en het β-proces β.
Het α-proces start (“output bij de start”) bij
<α<p1>><<α><q1>>
en genereert na enige tijd (“output na een tijd”)
<α<pi>><<α><qi>>,
waarbij pi en qi staan voor een
vectorvermenigvuldiging (of een OR die daar niet van verschilt) van i
metabolieten.
Analoog voor het β-proces waarvoor we superscript indexen
gebruiken: input <β<p1>><<β><q1>>
genereert na enige tijd output <β<pj>><<β><qj>>.
Indien er (operationele) interactie is tussen beide processen is
het onvermijdelijk dat dit gemodelleerd moet worden als een nieuw
proces, dus in een overkoepelende tralie. We kunnen nu twee
veronderstellingen onderzoeken: een van de processen is een
deelproces van het andere proces, of beide processen zijn
deelprocessen van een groter overkoepelend proces. Het
verschil kan als volgt operationeel vastgesteld worden: in het eerste
geval beïnvloedt het eerste proces het tweede en niet omgekeerd, dus
beide processen produceren output maar de output van het eerste
proces is ook input van het tweede proces. We zeggen ook: het eerste
proces is een regelaar van het tweede proces. In het tweede
geval beïnvloeden beide processen elkaar.
Het α-proces regelt het β-proces
Dit is de veronderstelling dat een <α<pi>><<α><qi>>
“als input” een <β<pj>><<β><qj>>
impliceert (“als output”). Dus de volgende goed gedefinieerde
welgevormde haakuitdrukking is ervaren:
<<α<pi>><<α><qi>>><β<pj>><<β><qj>>.
Dit is niet anders dan de uitdrukking van simultaneïteit.
Er geldt dus <β<pj>><<β><qj>>↔<α<pi>><<α><qi>><β<pj>><<β><qj>>
Beide processen regelen elkaar
Om dat te modelleren moeten we dus veronderstellen dat beide
processen “deelprocessen” zijn. In de totale tralie die beide
processen omvat en waarin de vluchtige laatst toegevoegde
onderscheiding bijvoorbeeld γ is, is dat proces niet meer monotoon
in α (die nu een gewone onderscheiding is, geen laatst
toegevoegde) en niet meer monotoon in β (zelfde reden). Operationeel
is dat zeer duidelijk: de elkaar uitsluitende toestanden die in het
overkoepelend proces optreden hoeven geen uitsluitende toestanden in
de deelprocessen te impliceren. De simultaneïteit (de vorm van tijd,
de elkaar uitsluitende processtappen) in het overkoepelend proces is
dus anders dan in de deelprocessen.
Dit heeft verrassende gevolgen want we kunnen nu een mogelijke
interactie modelleren door te veronderstellen dat voor een k en l met
k+l<i en voor een m en n met m+n<j geldt dat (input van het ene
proces is niet te onderscheiden van output van het andere proces)
<α<pk>><<α><qk>>↔<β<pm+n>><<β><qm+n>>
en
<α<pk+l>><<α><qk+l>>↔<β<pm>><<β><qm>>
Formeel dus door toepassing van de formele conjunctie en
transformatie:
<<<<α<pk>><<α><qk>>•<β<pm+n>><<β><qm+n>>>><<<α<pk+l>><<α><qk+l>>•<β<pm>><<β><qm>>>>>
Merk op dat door de uitdrukking als conjunctie de inputs en
outputs simultaan aanwezig zijn.
In woorden: een start-metaboliet van het α-proces (k<k+l)
is niet verschillend van een eind-metaboliet van het β-proces
(m+n>m) en tevens is een start-metaboliet van het β-proces
(m<m+n) niet verschillend van een eind-metaboliet van het
α-proces (k+l>k).
Dus in een meer vage taal gesteld: het α-proces veroorzaakt het
β-proces en het β-proces veroorzaakt het α-proces. Maar evenzeer:
het α-proces is het gevolg van het β-proces en het β-proces is het
gevolg van het α-proces. Menging van beide uitdrukkingen in die vage
taal is geen correcte weergave van de werkelijkheid aangezien dit een
taal veronderstelt die impliciet hetzelfde monotoon tijdsverloop
veronderstelt in het overkoepelend onderscheidingen universum als in
de deeluniversa (er wordt impliciet veronderstelt dat een oorzaak
voor een gevolg komt en een gevolg na een oorzaak zoals in één
spontaan proces). Het is operationeel duidelijk dat dit niet geldt.
Dit kan zeer abstract lijken maar een voorbeeld van twee
processen, die oorzakelijk perfect te volgen zijn maar niet in een
overkoepelend proces, vinden we in de optische illusies van de
Nederlander Maurits Cornelius Escher (1898-1972) die gebaseerd zijn
op de Penrose trap, een idee dat ze beiden samen ontwikkelden in het
midden van de 20ste eeuw.
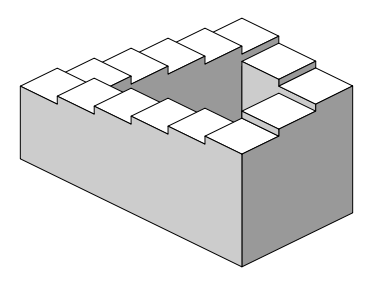
Deze
trap lijkt voor een willekeurig deelvolume van de ruimte een
werkelijke trap te verbeelden en men kan zich voorstellen dat een
figuurtje die trap oploopt. Maar die trap kan in werkelijkheid niet
gemaakt worden en geen enkel proces van dalen of stijgen op die trap
kan werkelijk uitgevoerd worden. Toch kan men zich inbeelden dat de
ene stap op de trap voor de andere stap op de trap ofwel dalen is,
ofwel stijgen.
Dat er zo iets moet gevonden worden (infimum in de ene, supremum
in de andere tralie) is onvermijdelijk omdat we anders geen
interactie operationeel zouden waarnemen: de waarneembare punten van
de interactie zijn gemeenschappelijk aan beide processen. In dat
overkoepelende universum zal er dus evenzeer gelden dat elk punt te
schrijven is als een transformatie van twee andere. We kunnen dus
altijd veronderstellen dat er punten zijn die zowel in het α-proces
(subscript) als in het β-proces (superscript) simultaan zijn.
Veronderstel dan twee punten die zowel een subscript als een
superscript hebben. Veronderstel dat p11 ↔
p22 •a1 en dat geldt dus in het
subscript universum, en p11 ↔ p22
•a1 en dat geldt dus in het superscript universum. Merk
op dat dus ook geldt: p22 ↔ p11
•a1 en p22 ↔ p11
•a1 en dus bijvoorbeeld p11 ↔
p11 •a1 •a1. Dit
laatste betekent onder andere dat dit geldt bij <<>>↔
a1 •a1. En dus a1↔a1.
Uit deze studie kunnen dus nieuwe inzichten ontstaan, bijvoorbeeld:
p11 •p22↔a1↔a1
en het linkerlid is, indien telbaar, een verhouding, in de twee
universa is dezelfde verhouding te vinden als een gegenereerd spoor,
bijvoorbeeld massa*afstand (dus eventueel een grotere massa op
kleinere afstand), een constant blijven van energie enz.... Dit maakt
dat ook interacties in de klassieke hypothese te modelleren zijn.
Beide bijkomende punten die hun universum karakteriseren (want p11
noch p22 kunnen hun universum karakteriseren
aangezien ze relevant zijn in beide universa) hebben dezelfde
ervaringswaarde, het zijn niet te onderscheiden sporen en ze geven
aanleiding tot een invariante
verhouding. Het nieuw proces, gebaseerd op de gemeenschappelijke
onderscheidingen is terug spontaan en gesloten. Dat betekent dus dat
ze kunnen gezien worden als karakteristieken van één universum, één
telbare entiteit: de relatie tussen beide processen. Voor die
entiteit en aan dat spontaan proces kan er terug een (monotone) tijd
verbonden worden, met vluchtige onderscheidingen bijvoorbeeld γ,
tijd die anders is dan de tijd van de deelprocessen. Dat (nieuw)
spontaan proces kan dan een oscillatie zijn rond een
evenwichtsgebied, oscillatie die gegenereerd wordt door het samenspel
van twee interagerende tijdsdimensies van de deelprocessen. Door het
begrip oscillatie te gebruiken drukken we uit dat het niet
noodzakelijk is dat twee interagerende processen ooit een evenwicht
bereiken. We tonen aan dat slechts vanaf drie interagerende processen
evenwicht
kan gemodelleerd worden.
We hebben hier dus de basis uitgetekend van de modellering in het
haakformalisme van de interactie van deelprocessen, en dit enkel voor
twee spontane processen. Dit is uitbreidbaar naar meerdere processen
en meer dan het creatief product en het vectorproduct is hiervoor
niet nodig.
Voorbeelden
In een mechanische slinger “veroorzaakt” de potentiële
energie de toename van de snelheid, en “veroorzaakt” de snelheid
het opbouwen van potentiële energie en wanneer de totale energie
geen andere processen voedt en daardoor dissipeert dan wordt er geen
evenwicht bereikt.
Een ruimtesonde kan versneld worden door zijn kinetische energie
te vergroten in het zwaartekracht veld van verschillende grote
massa's zonder dat de ruimtesonde op een van die massa’s neerstort.
Dit kost geen energie, het is enkel het omzetten van potentiële
energie naar kinetische energie. Dit kan enkel maar als er precies
genoeg kan gestuurd worden naar een doel.
De Belousov–Zhabotinsky reactiedynamiek, iconisch voorbeeld van
een niet-lineaire chemische oscillator die dank zij Ilya Prigogine
een theoretische modellering kreeg als een voorbeeld van een
“Brusselator”.
De prooi-predator relatie (Lotka–Volterra vergelijking enz...).
Leven is slechts mogelijk op een substraat van spontane processen.
Levende systemen blijven daarbij ver van evenwicht, de spontane
processen worden niet “tot het einde” doorlopen. Het
energieniveau blijft hoog, de exergie blijft hoog, informatie
(indien..., dan, …) gaat niet verloren. Levende systemen zoeken
actief interagerende processen zodanig dat ze andere spontane
processen gebruiken om ver van evenwicht en dus “ver van dood” te
kunnen blijven. Uiteraard zullen ze hierbij energie (en materie)
verbruiken en zullen ze dus effectief iets verliezen en als sporen
achterlaten omdat anders dat spontaan proces niet zou doorgaan, maar
het zijn de sporen die zorgen voor de interactie. In het verbruik van
energie staan ze soms in competitie met andere levende systemen maar
synergie is meer de regel dan de uitzondering. Synergie is een
voorbeeld van een positieve som interactie (in contrast met een
nulsom
en dus evenwicht), typisch door een toename van keuzemogelijkheden,
een groter universum dat dus meer onderscheidingen telt dan degene
die de beide deeluniversa operationaliseren, meer diversiteit waarin
meer simultaan kan gebeuren en er dus een win-win kan ontstaan.
Een positieve som interactie wordt gekarakteriseerd, niet alleen door
het niet verloren gaan van potentiële structuur, dus informatie,
maar door een toename van potentiële structuur dank zij de
interactie en creativiteit. Dit kunnen we ook beschrijven door de
redundantie van bronnen van entropieproductie. Stabiliteit
die dynamische verandering mogelijk maakt treedt enkel op als de tijd
meer bepaald wordt door energetische transformaties dan door
informatie transformaties. Levensvatbare systemen (“viable
systems”) zullen dus creatief zijn, divergerend, explorerend,
voortdurend op zoek naar nieuwe bronnen, niches, uitdagingen, kansen,
“affordances”. Soms moet dit snel gebeuren als er gevaar dreigt
en een dreiging moet verdwijnen in de omgeving. Dan zijn nieuwe
exploraties minder gepast. Soms kan dit minder snel en is er meer
focus op nieuwe kansen. Als ze niet creatief zouden zijn en niet
zouden exploreren naar andere middelen, als ze in die exploratie geen
nieuwe acties zouden ondernemen, dan zouden ze minder fit zijn in hun
omgeving, dan zouden ze in die omgeving niet overleven. Geen
activiteit is voor levende systemen geen optie: ze zouden spontaan
dood gaan. Levensvatbare systemen zijn altijd deelsystemen
en tezelfdertijd supersystemen van andere levensvatbare systemen.
