Er gebeurt ook altijd iets anders dan datgene waarvoor een agens kiest. Dit enige axioma heeft geleid tot de geordende begrippen “laatst toegevoegde onderscheiding” en grootste universum: “ervaren door een agens-in-context” gebeurt altijd in het grootste onderscheidingen universum van dat agens-in-context. Een gevolg hiervan is dat, als we een geordende reeks sporen van ervaringen beschouwen die in werkelijkheid doorlopen werden, dat dan elke andere denkbare (veronderstelde, gehypothetiseerde, …) geordende reeks sporen van ervaringen minstens voor één van de stappen in een kleiner onderscheidingen universum moet gemodelleerd worden. Dat kleiner universum kan geanticipeerd worden, maar kan niet voorspeld worden. Dat betekent dus dat het agens-in-context een voor hem/haar denkbaar kleiner onderscheidingen universum zal kiezen om te ervaren, ervaren dat dan blijkt te gebeuren in een groter (het grootste) universum. Maar dat betekent ook dat dit geldt voor elke andere agens-in-context, terwijl ook het grootste universum voor elke agens-in-context verschillend zal zijn. Een beetje uitdagend geformuleerd betekent dit dat elke agens-in-context “sneller is dan ik” (minder toestanden doorloopt, minder stappen doorloopt, spontaan minder oud wordt), maar dat dit ook geldt voor mezelf als agens-in-context voor een andere. Dit is niet paradoxaal (onder andere gekend als “de tweeling paradox” bijvoorbeeld).
We kunnen nu de gevolgen onderzoeken van de hypothese dat het grootste universum voor elke agens-in-context door dezelfde schaal voorgesteld kan worden, de grens van de waarnemingsresolutie die gedeeld wordt door elke agens-in-context, de hypothese van de speciale relativiteitstheorie.
Veronderstel dus één grootste onderscheidingen universum dat zijn rol speelt voor twee agentia-in-context A1 en A2. Dan moet dat betekenen dat er zowel voor A1 als voor A2 geldt dat het individueel werkelijk gevolgde pad meer sporen achterlaat dan het pad gevolgd door de andere Ai. Dit herkennen we in de relativiteitstheorie als het principe van de maximale veroudering: gelijk welk pad dat niet gevolgd wordt in een toestandsruimte met ordeningsparameter “tijd”, neemt minder tijd in beslag (heeft een kleinere eigen tijd) dan het werkelijk gevolgde pad, en dat geldt voor elke agens (de eigen tijd is een invariant voor elke Ai en wordt enkel bepaald door de beperkingen van uitsluiting die het aantal stappen van die specifieke Ai genereert).
We zullen nu het principe van maximale veroudering in het haakformalisme modelleren en volgen hiermee exact de inherente veronderstellingen en de methodiek zoals ze beschreven worden in de publicaties van Edwin Taylor en John Archibald Wheeler. We zijn immers in staat om zowel een ruimteafstand als een tijdafstand te modelleren in het haakformalisme en het is het nieuw geïntroduceerde getal m, de Lorentz invariant, die dit mogelijk maakt.
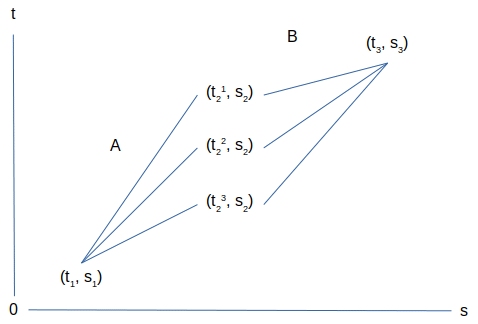
We beschouwen het volgende Minkowski diagram, diagram (een 1-splitsing) waarvan we de relevantie voor het haakformalisme al onderzocht hebben:

We veronderstellen twee gebeurtenissen (t1, s1) en (t3, s3) en we veronderstellen dat t1<t3. De ti zijn stappen van een ordeningsparameter die we nu interpreteren als “tijd”, maar die ook als een totaal geordende vrijheidsgraad kan geïnterpreteerd worden. De si zijn stappen van een ordeningsparameter die kan toenemen en afnemen die we nu interpreteren als een ruimte afstand, maar die ook als een energie kan geïnterpreteerd worden. We veronderstellen dat we tussen beide gebeurtenissen een gebeurtenis (t2, s2) zullen vinden. Dit is een belangrijke veronderstelling aangezien we hiermee het “gemiddelde” binnenbrengen en dat dit enkel voor intensiteiten kan, niet voor eenheden (die hier dan de schaalfactor zijn op elke as).
Deze gebeurtenis maakt het mogelijk om een metrisch interval A, tussen (t1, s1) en (t2, s2), en een metrisch interval B, tussen (t2, s2) en (t3, s3) te onderscheiden. We vragen ons nu af welk pad gevolgd wordt tussen de gebeurtenissen (t1, s1) en (t3, s3), concreet: welk punt van de volgende drie met zelfde s waarde: (t21, s2), (t22, s2), (t23, s2) behoort tot het pad?
We beschouwen nu het kwadraat van de eigen tijd τ2ij voor tijdsverschillen, die voor bijvoorbeeld interval A niet anders is dan (t2-t1)2-(n2-n1)2. Merk op dat de tijd hier als verschil aangegeven wordt en dus de ordening van de verschillen een belangrijke rol speelt. De hypothese maakt het mogelijk om één toestand als nulpunt en dus evenwichtstoestand te nemen. τ2ij=(t2-t1)2-(n2-n1)2 is niet anders dan een specifieke invulling van het meer abstracte 4(m+ni)(m+nj) en dit is op zijn beurt niet anders dan het verschil van kwadraten (2m+n1+n2)2-(n1-n2)2. Dus we stellen τ21=τA=((t2-t1)2-(n2-n1)2)½=((t2-t1)2-(s2-s1)2)½. Dit is een getalfunctie waarbij t1, s1 en s2 constanten zijn. We kunnen dus de afgeleide nemen naar t2. Deze klassieke infinitesimalen en afgeleiden hebben we ook in het haakformalisme gemodelleerd en voor de veronderstellingen verwijzen we dus naar daar. Dus dτA/dt2=(t2-t1)/((t2-t1)2-(s2-s1)2)½ en dit is niet anders dan (t2-t1)/τA. We berekenen ook de eigen tijd voor het interval B. Dus τ32=τB=((t3-t2)2-(n3-n2)2)½=((t3-t2)2-(s3-s2)2)½. Dit is een getalfunctie waarbij t3, s3 en s2 constanten zijn. We kunnen dus de afgeleide nemen naar t2. Dus dτB/dt2=-(t3-t2)/((t3-t2)2-(s3-s2)2)½ en dit is niet anders dan -(t3-t2)/τB.
Nu veronderstellen we dat we de eigen tijden van beide intervallen kunnen optellen zodanig dat we een totale eigen tijd specificeren als τTOT=τA+τB. Dit is een belangrijke veronderstelling en impliceert dat tijdsverschillen zich gedragen als ruimteverschillen wat dus impliceert dat er een nulpunt gekozen is. ΤTOT is een functie van t2 en bereikt een extremum (in dit geval een maximum) voor de afgeleide gelijk aan nul, dus voor dτTOT/dt2=τA/dt2+τB/dt2=0. Dat is niet anders dan (t2-t1)/τA-(t3-t2)/τB=0 of dus (t2-t1)/τA=(t3-t2)/τB. Dus de verhouding van het verschil van de gemeten tijdsintervallen tot de eigen tijd moet dezelfde zijn, welke keuze van tussenliggend punt we ook zouden maken en hoe A en B ook zouden verschillen of hoe ze zouden verschillen van een C, D, E, … intervallen tussen dezelfde twee gekozen gebeurtenissen. Als we de tijdsverschillen nu anders coderen dan moet dus gelden dat tA/τA=tB/τB=tC/τC=tD/τD=… waaruit we afleiden dat dit moet gelden voor een infinitesimale toename dt/dτ. Dus de τA=((t2-t1)2-(n2-n1)2)½=((t2-t1)2-(s2-s1)2)½ noteren we nu als τA2=tA2-sA2 en hieruit volgt dat voor een willekeurige afgeleide dτ2=dt2-ds2=dt2(1-ds2/dt2)=dt2(1-v2) volgens de klassieke visie van de snelheid als afgeleide naar een tijdsverschil van een afstandsverschil. Dus dt2=dτ2(1-v2)-1. Hieruit volgt dat dt/dτ=(1-v2)-½ en aangezien we aangetoond hebben dat dt/dτ een constante verhouding is, moeten we besluiten dat v constant moet zijn en het pad is het kortste tussen (t1, s1) en (t3, s3), namelijk een rechte lijn.
Uit het onderzoek naar het gevolg van tijdsverschillen.
Om dit aan te tonen brengen we de Lorentz referentie eenheid m als volgt in de getallen binnen: stel ti=ni+m en tj=-nj-m, zodanig dat ti-tj=2m+ni+nj. Dus de snelheid (ni-nj)/(ti-tj) is dezelfde als vij+m=(ni-nj)/(2m+ni+nj) en de eigen tijd is de negatieve versie van de eigen ij-tijd want 4(m+ni)(m+nj)=4(ti)(-tj). De wortel nemen uit een negatief getal vereist het mogelijk maken van √-1. Dat is wat men klassiek moet doen om een verschil te maken tussen “tijdsverschillen” en “ruimteverschillen” maar het gevolg is dan dat “tijd” een parameter is zoals “ruimte” en impliciet de hypothese uitdrukt dat men “terug kan gaan in de tijd”. Inderdaad: alle klassieke natuurwetten zijn symmetrisch voor omkering van het teken van de parameter tijd.
τ21=τA=((t2-t1)2-(n2-n1)2)½=((t2-t1)2-(s2-s1)2)½.
τ32=τB=((t3-t2)2-(n3-n2)2)½=((t3-t2)2-(s3-s2)2)½.
τ2ij+m=4(m+ni)(m+nj)=4(ti)(-tj)
τ221+m=4(m+n2)(m+n1)=4(t2)(-t1)
τ232+m=4(m+n3)(m+n2)=4(t3)(-t2)
Noem nu de constante (1-v2)-½ de verhouding E/M=(1-v2)-½ of E=M(1-v2)-½ en zo introduceert men de klassieke energie en de klassieke rustmassa in de veronderstelling dat c=1, de eenheid van snelheid. De verhouding E/M kunnen we ook gelijkstellen aan een verhouding μ/ν=(1-v2)-½ waarmee we (onder voorwaarde c=1) het verband gelegd hebben met de klassieke energie kunnen reconstrueren en de kinetische en potentiële energie kunnen onderscheiden.
Nu we ook de rustmassa een plaats gegeven hebben kunnen we uit het principe van de maximale veroudering de impuls afleiden. We laten ons inspireren door de volgende tekening waarbij we ons afvragen welke van de drie punten met zelfde tijd coördinaat op het pad tussen de gebeurtenissen (t1, s1) en (t3, s3) zal liggen:
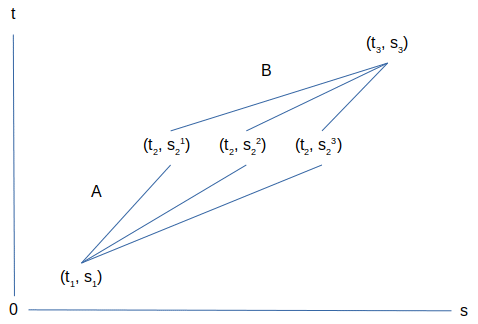
Dus τA=((t2-t1)2-(s2-s1)2)½. Dit is een getalfunctie waarbij t1, t2 en s1 constanten zijn. We kunnen dus de afgeleide nemen naar s2. Dus dτA/ds2=-(s2-s1)/((t2-t1)2-(s2-s1)2)½ en dit is niet anders dan -(s2-s1)/τA. We berekenen ook de eigen tijd voor het interval B. Dus τB=((t3-t2)2-(s3-s2)2)½. Dit is een getalfunctie waarbij t3, s3 en t2 constanten zijn. We kunnen dus de afgeleide nemen naar s2. Dus dτB/ds2=+(s3-s2)/((t3-t2)2-(s3-s2)2)½ en dit is niet anders dan (s3-s2)/τB. Als we de afstandsverschillen nu anders coderen dan moet gelden dat sA/τA=sB/τB=sC/τC=sD/τD=… waaruit we afleiden dat dit moet gelden voor een infinitesimale toename ds/dτ. Dus de τA=((t2-t1)2-(s2-s1)2)½ noteren we nu als τA2=tA2-sA2 en hieruit volgt dat voor een willekeurige afgeleide dτ2=dt2-ds2=dt2(1-ds2/dt2)=dt2(1-v2) volgens de klassieke visie van de snelheid als afgeleide naar een tijdsverschil van een afstandsverschil. Dus dt2=dτ2(1-v2)-1 en dus 1/dτ2=1/dt2(1-v2)-1 en ds2/dτ2=ds2 /dt2(1-v2)-1. Dit is niet anders dan v2(1-v2)-1. Hieruit volgt dat ds/dτ=v(1-v2)-½ en dit is een constante zoals we aantoonden en de verhouding impliceert een rechte lijn. We kunnen deze constante als de impuls herkennen voor een eenheidsmassa en dus kunnen we de intensiteit van de rustmassa M noemen en Mv(1-v2)-½ is een constante.