De onzekerheidsrelatie van Heisenberg kan in het haakformalisme gemodelleerd en begrepen worden door de tralie van de klassieke hypothese en de tralie van de kwantum hypothese met elkaar te vergelijken.

1. Bij het klassieke model wordt de laatst toegevoegde onderscheiding niet ingebouwd in de tralie, de waargenomen entiteit is dan een atoombuur en stellen we voor als <a_i><<a>_i> met elke a_k een ingebouwde onderscheiding, met k tot i-1, en de waargenomen toestand is ofwel <<a>_i> in conjunctie met de laatst toegevoegde onderscheiding ofwel <a_i> in conjunctie met de laatst toegevoegde onderscheiding. Essentieel is dat beide suprema uit exact hetzelfde aantal onderscheidingen opgebouwd zijn (aantal gelijk aan i). De beide toestanden (<<a>_i> versus <a_i>) zijn perfect complementair. Men schakelt tussen beide toestanden door elke onderscheiding te vervangen door zijn inbedding. Er is geen onzekerheid aangezien beide opgebouwd zijn met hetzelfde aantal onderscheidingen, namelijk i. De tralie kan dus opgebouwd worden zowel met de atomen als met de atoomburen. Wat er gemodelleerd wordt is het gedrag van iets dat perfect gekend is.

2. Bij het kwantum model heeft de laatst toegevoegde onderscheiding meerdere aspecten waarbij er enkele in de tralie ingebouwd worden, zonder dat a priori bekend is welke aspecten ingebouwd worden. Het resultaat hiervan is dat de waargenomen entiteit zich op een a priori ongekende diepte bevindt in de tralie (en dus geen atoombuur is) en dat de toestand waarin de entiteit zich bevindt slechts na de waarneming kan afgeleid worden. Die entiteit kunnen we dan voorstellen als de nevenschikking (niet verschillend van het vectorproduct) A_iA_j met elke A_k een mogelijk waar te nemen toestand van de entiteit en de waargenomen toestand is ofwel een van de A_i ofwel een van de A_j. Essentieel is dat de aantallen i en j kunnen verschillen van elkaar (maar ook niet moeten verschillen van elkaar). Hoe minder atomen zich in de disjunctie A_i bevinden, hoe meer in A_j (want dat zijn de enig mogelijke waarneembare toestanden) en hoe onzekerder het is welke A_k zal waargenomen worden, en uiteraard geldt de omgekeerde relatie ook. De maximaal mogelijke diepte wordt bereikt bij de disjunctie van alle waarneembare toestanden (dat aantal is de som van de A_i en de A_j) en de log₂ van dat aantal geeft meteen ook het aantal onderscheidingen van de tralie.

Alle mogelijke maten die voor de a priori onbekende diepte kunnen verzonnen worden zullen allemaal gebaseerd zijn op de metriek inherent in de niveauverschillen van de tralie en dus ook in het aantal toestanden van de tralie. Dit zijn allemaal mogelijkheden om de onzekerheidsrelatie te kwantificeren. Een voorbeeld hiervan (dat Heisenberg gebruikte) is de spreiding op beide waarnemingen.

We kunnen dit ook op de volgende manier zien aan de hand van een voorbeeld: neem de vier toestanden die elkaar uitsluiten in een twee onderscheidingen universum en interpreteer deze als vier mogelijke posities, de processnelheden worden nu gedefinieerd vanuit het verschil van toestanden, dus zijn ze gerelateerd met de punten op een niveau lager: daar zijn 6 mogelijkheden en geen vier.

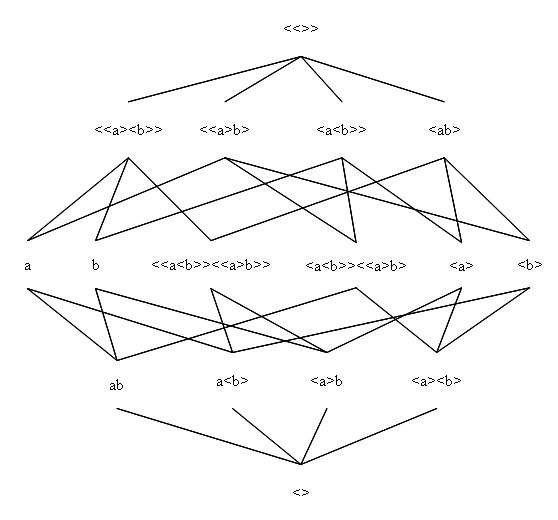
De exacte bepaling van één van deze punten op het centraal niveau komt overeen met de vaststelling dat deze door twee mogelijke posities gerealiseerd wordt. De exacte bepaling van één van de toestanden komt overeen met de vaststelling dat de toestand drie mogelijke processnelheden realiseert.

Er zijn in de tralie verschillende deeltralies te onderscheiden die als 1-splitsing kunnen beschouwd worden en dus isomorf zijn met de structuur van de tralie van de klassieke hypothese. Maar ze hebben niet de eigenschap van de klassieke hypothese dat de toestanden door inbedden van elke onderscheiding in elkaar om te zetten zijn, bijvoorbeeld in de 1-splitsing supremum <<>>, centraal niveau <<a><b>> en <<a>b>, en infimum a zijn de twee toestanden niet op die manier in elkaar om te zetten.

We kunnen dit ook als volgt inzien: elk potentieel waar te nemen punt is als een positie in een Euclidische ruimte met drie cartesiaanse componenten te modelleren. Maar de gebruikte symbolen hebben een relatieve betekenis, we kunnen immers ook de volgende vertaling uitvoeren: a•b↔C, a•c↔B, b•c↔A, en dus ook voor de inbeddingen: <a>•<b>↔C, <a>•<c>↔B, <b>•<c>↔A. Hierbij geldt dat A•B↔C, A•C↔B, B•C↔A enz.... Dus hetzelfde punt is louter vanuit processnelheden op te bouwen. Dus de klassieke hypothese is zowel voor posities als voor snelheden geldig, de kwantum hypothese zal voor beide onzekerheid opleveren.