In het algemeen is waarnemen zeer complex. Hoe krijgen mensen dan een exacte, betrouwbare, herhaalbare beoordeling van een situatie die kan gestuurd worden naar een doel? Dit is een uitermate belangrijke problematiek in een technische wereld, die op zich reeds een complexe wereld is, en waarin alles juist draait rond die extreme betrouwbaarheid.

Van bij het begin van de technische cultuur hebben ontwerpers, die later ingenieurs genoemd werden, onderzocht hoe de informatieverwerking voor controleurs van processen sterk kan vereenvoudigd worden (codering) om de uitvoerder niet te veel te belasten met irrelevante stimuli zodanig dat hij een exacte, betrouwbare controle kan uitvoeren. Hierbij is geprobeerd de globale mentale belasting die normalerwijze in een technische context optreedt te verminderen. Men zag toen geen andere weg dan de controleurs een doorgedreven technische training te geven omdat de techniek prioriteit kreeg op de mens. Dit leidde tot het ontstaan van specifieke technische scholen in de loop van de 19de eeuw. Inzicht in de controlemogelijkheden van mensen is dus steeds een bijzonder aandachtspunt geweest voor ingenieur-ontwerpers. Maar de technische cultuur had ook voor gevolg dat de technisch geconstrueerde wereld relevant werd voor meer en meer mensen. Stilaan werd het duidelijk dat het ondoenbaar is om alle mensen technisch te scholen. Van meer recente datum is het inzicht doorgedrongen dat ook de manier om informatie te coderen aangepast moet zijn aan de gebruikers, of zij nu de technische modellen begrijpen of niet (denk maar aan het programmeren van een thermostaat, of aan de gebruiker die iets wil opladen in het geheugen van een mobiele telefoon). We kunnen ons nu geen wereld meer voorstellen zonder een grondig begrijpen van het begrip "informatie".

Coderen is relevante informatie waarneembaar maken voor de stakeholder die hiermee iets zal willen anticiperen. Coderen is altijd onvolledig: het is een werkelijkheid afbeelden (veel-op-een transformatie) in een beperkt model voor die werkelijkheid dank zij goed geselecteerde sporen. Controleren is, dank zij sporen die enigszins permanent zijn, informatie met andere informatie vergelijken. Men zoekt of men een onderscheid, een verschil kan vinden. Dikwijls moet men geen volledig model hebben van de informatie om toch verschillen te kunnen onderscheiden. Informatie is een verschil dat relevant is, dat zin heeft in een specifieke context, is een verschil dat "een verschil maakt".

De eerste noodzakelijke stap om informatie te coderen is te onderzoeken op hoeveel punten een verschil kan en moet gemaakt worden. Dat betekent dat men zijn aandacht richt op de relevante toestandsruimte van systeem en regelaar. Elke toestand in de toestandsruimte wordt klassiek beschouwd als een verschillende combinatie van waarden van basisvariabelen of aspecten die op dat ogenblik gerealiseerd zijn in die unieke toestand (en dat noemen we dan een volledig relevant model voor die toestand in die context). Elke toestand sluit een andere uit. We kunnen de onderscheiden toestanden tellen en dus een maat krijgen voor de toestandsruimte. Deze maat wordt in de cybernetica de verscheidenheid V genoemd (Variety). Het groot aantal toestanden van het systeem proberen ingenieur-ontwerpers af te beelden op een beperkt aantal toestanden die door de regelaar kunnen ingenomen worden.

Voorbeeld 1:

We beschouwen twee displays die een toestand van een machine coderen.

Display 1 kan drie waarden aannemen (bijvoorbeeld: laag, midden, hoog).

Display 2 kan vier waarden aannemen (bijvoorbeeld: ←, ↑, →, ↓).

In totaal kunnen we hiermee 3 x 4 = 12 toestanden van de machine voorstellen. De maat van de toestandsruimte kunnen we hier als 12 nemen. We zullen verder zien dat we deze maat nog verder moeten verfijnen. Impliciet gaan we hier immers van uit dat er geen andere coderingen kunnen gebruikt worden. Bijvoorbeeld geven de displays altijd een waarde aan (dus de display die geen waarde aanduidt geeft geen toestand aan) en de enige waarden die mogelijk zijn, zijn de hoger vermelde. De display 2 kan bijvoorbeeld niet uitdrukken dat de machine zich in een toestand “← of ↑” bevindt. De machine bevindt zich altijd in één van de vier voorgestelde toestanden en elke toestand sluit elke andere uit. Zo ook kan display 1 niet uitdrukken dat de machine zich in de toestand “midden of hoog” bevindt.

Voorbeeld 2:

We beschouwen een display met drie lichten die ofwel aan, ofwel uit zijn.

Hiermee kunnen we 2³ toestanden coderen.

Twee identieke display kunnen nu 8x8 = 64 toestanden coderen.

Uiteraard zijn we niet beperkt tot het gebruik van lichten. Elk binair mechanisme vertoont dezelfde mogelijkheden. Het grote verschil met deze binaire manier van coderen is nu dat er werkelijk op onderscheid kan gecodeerd worden. Het al dan niet aanwezig zijn van een licht kan nu werkelijk als een eenheid gezien worden, het is een minimaal verschil. Dit kon niet gezegd worden van bijvoorbeeld een eenheid gevormd door "laag" en "midden".

Merk op dat "midden of hoog" dat niet kon gecodeerd worden door display 1 van het eerste voorbeeld, nu wel kan gecodeerd worden als (bijvoorbeeld)

Uiteraard zijn nog verdere verfijningen mogelijk, waar we nu niet op ingaan.

Voorbeeld 3:

In het onderzoek naar het gedrag van mensen met een nieuwe staanlamp zou men volgende categorieën kunnen onderscheiden:

1. Ervaring met de bediening van lampen

2. Ervaring met de bediening van fluorescentie lampen

3. Ervaring met de bediening van LED's

Elke categorie kan nu in individuele klassen onderverdeeld worden (bijvoorbeeld op basis van het aantal keer dat men de lamp per week bedient).

De toestandsruimte is nu veel complexer aangezien bijvoorbeeld iemand die ervaring heeft met de bediening van fluorescentie lampen, ook ervaring zal hebben met de bediening van lampen en hij in de loop van de tijd zal experimenteren met het bedienen van LED's naar analogie met het bedienen van andere lampen.

In praktijk zal blijken dat men zich steeds zal moeten beperken tot het beschouwen van klassen waarin het gedrag kan ondergebracht worden of niet. Twee toestanden, gevormd door juist dat ene binaire verschil dat een verschil maakt kunnen nu beschouwd worden als op een meeteenheid van elkaar verwijderd. Immers: stel dat het systeem maar twee verschillende toestanden kan innemen, en er dus maar één onderscheid kan gemaakt worden, dan kan men dit onderscheid als eenheid van meting gebruiken. Het is juist dat onderscheid dat ons interesseert, eerder dan de "absolute" waarde van het aantal toestanden en in dit geval is dus V = 1. Deze meeteenheid noemt men de bit.

Gemeten in bits wordt de verscheidenheid dan gegeven door V = log₂N (met N het aantal alternatieve toestanden). Stel dat we N binaire onafhankelijke variabelen zouden hebben (bijvoorbeeld "iets" en "iets anders dan iets") dan is V = log₂(2^N) = N. Het is duidelijk dat in praktijk niet alle variabelen binair (rekening houdend met het minimale verschil) of onafhankelijk (zie voorbeeld 3) zullen zijn.

De verscheidenheid is een maat voor de mogelijkheid dat het beschouwde systeem heeft om een bepaalde toestand in te nemen, en is dan ook een maat voor de onzekerheid die wij hebben over de toestand in welke het systeem zich bevindt. Hoe groter de toestandsruimte, hoe onzekerder we zijn dat het systeem zich in een bepaalde op voorhand gekende toestand bevindt.

De binaire manier van werken laat ons toe enkel met verschillen te werken en kan dus gezien worden als een bevrijding van de gedetailleerde kennis die vanuit een absolutistisch standpunt zou geëist kunnen worden.

Bijvoorbeeld: een aalbes ontstaat eerst als een klein groen bolletje, en rijpt slechts als hij groter geworden is: de bes wordt dan een rode bol. We onderscheiden voor dit voorbeeld maar twee toestanden van grootte (klein en groot, dit enkel ten opzichte van elkaar) en maar twee toestanden van kleur (groen en rood, dit ook enkel ten opzichte van elkaar). Het is duidelijk dat dit een binaire vereenvoudiging is van de werkelijkheid. Maar nu is het voor iedereen die bessen kent ook duidelijk dat twee mogelijke toestanden uiterst zelden optreden: groene grote en kleine rode bessen komen niet voor als een mogelijke toestand in die toestandsruimte. Beide variabelen zijn niet onafhankelijk van elkaar, de totale verscheidenheid is maar een bit in plaats van twee.

Indien de totale verscheidenheid kleiner is dan de maximale verscheidenheid die we zouden voorzien, dan is er ergens een beperking in het systeem. Een beperking is een uitdrukking van de afhankelijkheid van variabelen van elkaar. Een bepaalde waarde voor een variabele legt de waarde van een andere variabele vast. Een beperking kunnen we dus kwantificeren als het verschil V_max - V.

Een beperking vermindert onze onzekerheid over de toestand waarin het systeem zich bevindt, en laat ons toe om te anticiperen: indien we een kleine aalbes vinden zal die groen zijn.

Voorbeeld

Kunnen we de display van het voorbeeld 1 coderen met de drie lichten?

Inderdaad. De veronderstelling van display 1 is dat er altijd een licht oplicht en dat er nooit twee lichten tezelfdertijd oplichten.

Het zijn dus enkel rij twee, drie en vier die aan die voorwaarden voldoen, en we krijgen inderdaad de mogelijkheid drie verschillen te coderen.

De beperkingen die door de veronderstellingen ontstaan zijn kunnen we nu kwantificeren als de maximale min de feitelijke verscheidenheid, dus als 8-3 =5 .

Hetzelfde bereiken we in de veronderstelling dat de lichten opeenvolgend aan en uit gaan:

Dit is een minder grote beperking aangezien de verscheidenheid nu 8-4=4 is.

Deze laatste soort codering is de codering die we aantreffen bij wijzerplaten

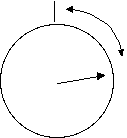
En ook bij parameter balken.

Entropie

Conant en Ashby bewijzen dat een keuze criterium om onze pogingen van het regelen van sporen van processen te klasseren van goed naar beter gegeven wordt door de informatie entropie van de waarschijnlijkheidsverdeling van de sporen: de beste keuze komt overeen met een zo laag mogelijke entropie. Het bewijs zullen we hier niet modelleren in het haakformalisme omdat we verschillende modellen kunnen inzetten. Dit is ook rechtstreeks duidelijk als men beseft dat de hoogste entropie bereikt wordt als alle sporen even waarschijnlijk zijn. De laagste entropie wordt bereikt voor een unieke (r_i⊗s_j)_ek, met andere woorden voor elke interactie, die we dus voorstellen als (r_i∩s_j), is er maar één e_k. Dus als we s_j gegeven veronderstellen, dan mag in de kolom van een bepaalde j slechts één e_k optreden (dit is een uniek spoor) en moet de waarschijnlijkheid van de andere (r_i∩s_j) nul zijn. Analoog: als we r_i gegeven veronderstellen, dan mag in de rij van een bepaalde i slechts één e_k optreden en moet de waarschijnlijkheid van de andere (r_i∩s_j) nul zijn. Dus voor een bepaalde s_j geldt dat er geen sporen ontstaan bij de conjunctie van elke toestand van de regelaar behalve 1, dus enkel één (r_i∩s_j) genereert een spoor. Dat spoor is dan simultaan met beide atomen en kan niet onderscheiden worden van een van de atomen, dus ofwel r_i ofwel s_j.

Met ons eerste voorbeeld dat we in tabel vorm hieronder nog eens herhalen veranderen we de regelaar zodanig dat aan de voorwaarde van minimale entropie voldaan wordt

Een mogelijk resultaat is:

Merk op dat we de waarschijnlijkheid van optreden van toestanden van S niet veranderd hebben, de regelaar zal met zekerheid 25% van de systeem toestanden selecteren in de ene regeltoestand en 75% in de tweede regeltoestand. De reden waarom we dat resultaat gekozen hebben kan niet anders zijn dan dat de regelaar één relevante switch maakt tussen de toestanden in S die binnen of buiten G vallen, en dit voorbeeld zijn er 25% toestanden binnen (buiten) G en 75% toestanden buiten (binnen) G. Merk op dat de regelaar één relevante toestand heeft voor elke toestand in S die binnen/buiten G valt. Het is dus een perfecte regelaar. Merk op dat de regelaar switcht tussen een welgevormde haakuitdrukking en zijn inbedding, hij voert dus een uitwendige involutie uit.

In werkelijkheid zijn perfecte regelaars onmogelijk aangezien er ook altijd iets anders zal gebeuren dan datgene dat de regelaar doet gebeuren. Als we creatief genoeg zijn dan zullen we wel onderscheidingen kunnen maken in dat andere dat gebeurt. Echter ook dan, ook als we het onderscheidingen universum groter maken, toch zal er ook altijd iets anders gebeuren dan datgene dat de regelaar doet gebeuren, regelaar die kan regelen in dat grotere universum.

Praktische toepassingen

De volgende stappen leiden tot een bepaling van de relevante toestandsruimte van een regelbaar proces.

1. Onderscheid de inputs die te kiezen zijn (ze zijn immers de voorspelbare output van de regelende actie).

2. Op welk niveau van intensiteit zijn deze inputs te kiezen.

   1. Nominaal: bijvoorbeeld: “aan” versus “uit”, “aanwezig” versus “afwezig”

   2. Ordinaal: bijvoorbeeld: minder versus meer “aan-uit/aan-af-wezig aspecten” die zich in een binair af te beelden toestand kunnen bevinden

   3. Interval: bijvoorbeeld: een “aan-uit” aspect is te regelen in stappen die additief zijn, waarbij één stap dezelfde eenheid is

   4. Ratio: bijvoorbeeld: bovendien neemt ofwel “aan” of “uit” een nulpunt in waarbij het aspect irrelevant wordt.

3. Welke processen zijn hiermee verbonden en welke outputs veranderen hierdoor (maak een schema met feedback loops)

4. Kwantificeer de verdubbelings-(halverings)-tijden van de loops

5. Bepaal wanneer actie moet ondernomen worden om ongewenste aspecten te vermijden of gewenste aspecten te bereiken

6. Welk niveau van intensiteit is relevant in de zo gedefinieerde toestandsruimte

7. Bepaal hoe die relevante informatie (zowel de niet te kiezen output als de te kiezen input) redundant aangeboden kan worden in het verwachtingspatroon van de stakeholder die beslissingen moet nemen om het proces te sturen

8. Test en leer uit wat er gebeurt