Voor doelgerichte processen hebben we een minimale veronderstelling moeten aannemen: de intensiteit van een gebeurtenis kan enkel geanticipeerd worden ten opzichte van de intensiteit van de processtap nu. Die anticipatie kan dan in werkelijkheid blijken gepast te zijn of niet. Die minimale veronderstelling leidt dan tot een positieve feedback (weg van een anti-doel) ofwel een negatieve feedback (naar een doel). In werkelijkheid zal dan een proces plaatsvinden dat op voorhand kan beschreven worden als een onbekende functie (x-x0)t+Δt=f(t, k, (x-x0)t) die slechts a posteriori kan opgesteld worden.
Een volgende veronderstelling is dat processen op zodanige manier kunnen interageren dat een evenwicht ontstaat. Een dynamisch evenwicht (een steady state) kunnen we modelleren door een normalisatie die het resultaat is van positieve en negatieve feedback processen.
We tonen nu aan dat we hiermee ook een oscillerend proces rond de steady state kunnen modelleren.
We kunnen dit met behulp van één parameter θ die zich ofwel in de lading van de normalisatiefactor manifesteert, ofwel in de eigenwaarde, en waarbij sin2θ+cos2θ=1.
Een eigenwaarde werd geïntroduceerd als een metrische factor tussen een welgevormde haakuitdrukking en het verschil met een andere die de eerste uitsluit. Nemen we als tweede welgevormde haakuitdrukking de waarde <<>>, dan is uitsluiting altijd gegarandeerd. We kunnen nu stellen dat, met n het totaal aantal bits waarmee een entiteit kan voorgesteld worden, elke bit een individuele oscillatie kan vertonen als een intensiteit. Inderdaad, neem
cosθ = (n-m-p)1/2(n-m)-1/2
sinθ = p1/2(n-m)-1/2
We beschouwen nu het speciaal geval n-m=1 en dat betekent dat alle bits gemeenschappelijk zijn behalve één. Die heeft dan de intensiteit p. En in het veronderstelde geval is dat de maat van het interval tussen een toestand en <<>> en is daardoor ook de lengte van een projector.
Dit is altijd mogelijk. Noem nu x=cosθ en y=sinθ, dan kunnen we de volgende vermenigvuldiging begrijpen als een "patroon" van een som van kwadraten, wat een volgende abstractie is: (a2+b2)(c2+d2) = x2 + y2 en het rechterlid is dan per constructie gelijk aan 1 en in het algemeen geval kunnen we met zo'n patronen alle getallen construeren.
Oscillaties kunnen we ook modelleren door in de spontane dynamiek nog een veronderstelling bij te voegen. We nemen nu aan dat we in staat zijn de geanticipeerde toestand (dit is feedforward) van de dynamiek effectief in te nemen, dus dat we in staat zijn het verschil met het doel of anti-doel D van de geanticipeerde afwijking effectief te reduceren van zodra het waargenomen wordt. We modelleren dat met behulp van de volgende tabel waarin we bij elke stap niet vertrekken van het oorspronkelijk referentiepunt (namelijk het verschil dat een verschil maakt en dat we willen behouden en dus de niet veranderende entiteit), maar van een evoluerend referentiepunt dat bij elke tijdstap in staat is de intensiteit (het verschil met het doel) tot nul te reduceren. De tabel bouwen we dus op door bij de volgende stap de vorige stap tot nul te herleiden bij de sommatie.
Tijdstip |
Positieve feedback |
Geen feedback |
Negatieve feedback |
0 |
(x-x0) |
(x-x0) |
(x-x0) |
1 |
0(x-x0)+k(x-x0)=(x-x0)(0+k)=+k(x-x0) |
0 |
0(x-x0)-k(x-x0)=(x-x0)(0-k)=-k(x-x0) |
2 |
0(x-x0)(0+k)+k{(x-x0)(0+k)}=+k2(x-x0) |
0 |
0(x-x0)(0-k)-k{(x-x0)(0-k)}=+k2(x-x0) |
3 |
0(k2(x-x0))+k(k2(x-x0))=+k3(x-x0) |
0 |
0(k2(x-x0))-k(k2(x-x0))=-k3(x-x0) |
... |
... |
... |
... |
n |
kn(x-x0) |
0 |
(-k)n(x-x0) |
(x-x0)kn is niet anders dan (x-x0)en.lnk.
(x-x0)(-k)n is niet anders dan (-1)n(x-x0)en.lnk.
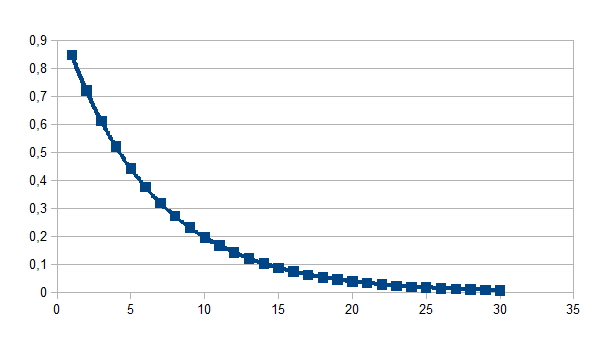
Met 0<k<1 is de positieve feedback niet anders dan het patroon van een negatieve feedback in de negatieve zin voor 1-(1-k)n. Hieronder geven we de grafiek van (x-x0)kn voor k=0,85 en 30 stappen naar het doelpunt 0:

Dat is dus een negatieve feedback die steeds dichter het doelpunt 0 benadert maar het nooit kan bereiken, het eenheidsverschil (x-x0) is altijd in enige mate (een kleine intensiteit) aanwezig. Dit doelpunt is dus het verschil met het doelpunt D zodanig dat we de vergelijking ook kunnen schrijven als D+1-(1-k)n. We kunnen dus zeggen dat het verschil met D altijd kleiner wordt. Eens men dus een actie kan nemen om het verschil met een doel D tot nul te herleiden (het nieuw doelpunt) dan leiden zowel positieve als negatieve feedback naar dat nieuw doelpunt. Zowel positieve als negatieve feedback vertonen dan het gedrag van de negatieve feedback.
Met -1<k<0 en dus negatieve feedback treedt een nieuw patroon op: oscillatie rond het doelpunt, het eenheidsverschil (x-x0) is hier ook altijd in enige mate (een kleine intensiteit) aanwezig.. Hieronder geven we de grafiek voor k=-0,85 en 30 stappen naar het doelpunt 0:
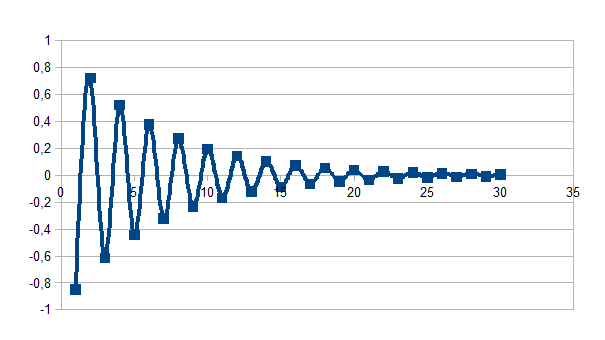
Eens een agens in staat is een actie te ondernemen om het verschil met een doel D te reduceren zullen zowel positieve feedback als negatieve feedback naar dit doel leiden. Positieve feedback benadert het doel langs één kant, negatieve feedback leidt tot oscillatie rond het doel. Een klassiek voorbeeld hiervan is een warm water douche waar de warmtebron ver verwijderd is van de douchekop: door de actie zelf van sturing op basis van actuele waarnemingen van temperatuur van het water onder de douchekop (en niet van geanticipeerde potentiële waarneming) is het nagenoeg niet te vermijden dat het systeem zal oscilleren tussen te koud en te warm.
Hiermee modelleren we de proportionele regeling van een proces: de aanpassing is proportioneel met de afwijking met het doel die bij elke tijdstap waargenomen wordt. Meer complexe acties (bijvoorbeeld door rekening te houden met buffering, met de aanpassingen die in het verleden gebeurd zijn en/of door toekomstige afwijkingen van het doel te anticiperen) kunnen gemodelleerd worden door het blijvend verschil (x-x0) en de eigenwaarde k aan te passen. Deze aanpassingen zijn dus afhankelijk van een “indien... dan...” constructie van de veronderstelde stabiele entiteit naar het verleden en naar de toekomst toe. Een technische realisatie hiervan is gekend als PID-regelaar. De letters PID staan voor Proportioneel, Integrerend (rekening houdend met de hypothetische modellering van verleden eigenschappen van de entiteit) en Differentiërend (rekening houdend met de hypothetische modellering van verwachte veranderingen van de entiteit).
Het aanpassingsvermogen van een agens (soms “complex adaptief systeem” genoemd of CAS) kan er dus toe leiden dat een doel altijd kan bereikt worden tot het verschil niet meer waarneembaar is voor die agens in die context. Dit is de manier waarop we een deterministisch veranderende werkelijkheid (dus niet waarneembaar afwijkend van een bekend doelpunt) in het haakformalisme kunnen modelleren.