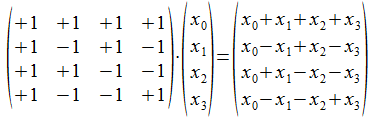
Bij de studie van de matrix vermenigvuldiging in het 1-splitsing universum hebben we begrepen dat deze in het haakformalisme overeenkomt met het creatief product. De actie van een operator uit het 1-splitsing universum op een splitsing voorgesteld als kolom of rij komt overeen met het toevoegen van één onderscheiding. Wanneer dit de laatst toegevoegde onderscheiding is dan is hiermee een evolutie in de tijd te modelleren. Hiervoor kan maar één maal vrij gekozen worden. Een tweede splitsing kan niet meer ongekend zijn, maar is afhankelijk van het herkennen van de lengte 2^n-1 die door het agens kan opgespannen worden, agens die de string probeert te kennen. Dit is wat we herkennen in de dan opgespannen welgevormde onderscheiding met p en q van lengte 2^n-1: <x<p>><<x><q>>. Dit is wat we onderzoeken in het 2-splitsing universum, die daardoor fundamenteel verschilt van het 1-splitsing universum.

We hebben gezien dat operaties in het 2-splitsing universum twee onderscheidingen kunnen toevoegen en op die manier een heel twee onderscheidingen universum.

Een concreet voorbeeld van toepassing van een 2-splitsing vonden we terug in de Hadamard transformatie H₄ die de basis van het twee onderscheidingen universum op centraal niveau omzet in een basis op atomair niveau. We pasten hiervoor H₄ toe op een kolom vector met vier componenten en merkten op dat de sommen in de resulterende kolomvector sterk te reduceren waren.

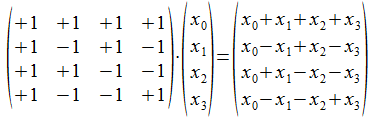
We kunnen nu nog een stap verder gaan en opmerken dat coëfficiënten van die basissen ook op een coherente manier mee transformeren, waarbij de coëfficiënten haakuitdrukkingen kunnen zijn. Inderdaad is de volgende tabel met de sommen uit de kolom matrix te construeren waarbij we van een vector in de basis {<<a><b>>, <a<b>>, <<a>b>, <ab>} naar een vector in de basis {<>, a, b, a•b} gaan en omgekeerd:

Omgekeerd gaat in de volgende tabel een vector in de basis {<>, a, b, a•b} naar een vector in de basis {<<a><b>>, <a<b>>, <<a>b>, <ab>}.

Merk op dat de viertallen (<<a><b>>, <a<b>>, <<a>b>, <ab>) en (<>, a, b, a•b) welgevormde haakuitdrukkingen zijn. De resulterende haakuitdrukkingen kunnen geïnterpreteerd worden als gedefinieerd in zes onderscheidingen: {h₁, h₂, h₃, h₄, a, b}, maar dat moeten we niet doen, we kunnen de h_i bijvoorbeeld met meer onderscheidingen voorstellen of met minder, of zelfs enkel met de onderscheidingen a en b. Dit is immers het grote voordeel van de ontwikkeling van het operator model van het haakformalisme: we kunnen operaties definiëren in ongekende universa.

In elk geval moeten we een beslissing nemen en de beslissing ligt voor de hand om een gekend universum als referentie te nemen, dus een opgespannen door a en b, en verder geen eisen te stellen aan de h_i. Dit maakt het duidelijk dat we met die beslissing, en dank zij de vier operatoren van het 2-splitsing universum, een twee-onderscheidingen-structuur zullen opleggen aan een willekeurig universum.

Van dit laatste geven we nu een aantal eenvoudige voorbeelden waarin we keuzen zullen maken voor de h_i in een universum opgespannen door a en b. Eerst zullen we de h_i afbeelden op individuele bits (in plaats van aan elke h_i een structuur toe te kennen en zo het twee onderscheidingen universum te verlaten) om zo de meest primitieve directe som te construeren van gecollapste atomen. Dit is expliciet uitgeschreven in de derde kolom, en in de vierde kolom zijn enkel de betekende bits overgenomen, die dan in de vijfde kolom afgebeeld worden op de bekende symbolen van het twee-onderscheidingen universum.

We herkennen dat we op die manier enkel en alle basisvectoren van het twee-onderscheidingen universum bereiken. Met de operatoren van het 2-splitsing universum kan men dus zelfs met individuele bits een tralie construeren die isomorf is met de tralie van het twee-onderscheidingen universum. Immers: elk punt van het twee onderscheidingen universum kan geschreven worden als een som van de vier basis operatoren uit de laatste kolom. Dit geldt dus ook voor de vier basisoperatoren in de eerste kolom.

Dit geldt wat ook de aard van de betekende bits zou zijn die in de vier componenten van de directe som naar voor komen, wat we in onderstaande vereenvoudigde tabel illustreren voor de keuze van een basisvector patroon.

Voor de keuze van een atoompatroon merken we dat er slechts drie gelijkaardige atomen gegenereerd worden (in dit voorbeeld zijn het drie AND-atomen en één OR-atoom, en dus niet de vier gelijkaardige atomen).

Dit legt onmiddellijk de relatie bloot met het creatief product patroon. We herkennen immers onmiddellijk dat de vier operatoren het 3&1 patroon zullen opdringen aan gelijk welke keuze van (+h₁, +h₂, +h₃, +h₄), waarbij dan zelfs de omweg langs orthogonale h_i niet nodig is.

Het is ook mogelijk om gecollapste tralies terug te vinden. Hierin wordt een rol toebedeeld aan de projectoren die de collapst realiseren. We geven eerst een voorbeeld van projectoren op centraal niveau <>⊕<a> en <>⊕a. Allen b blijft hier over als basis van het een onderscheiding universum.

Iets gelijkaardig realiseren we met de vier projectoren op atomair niveau:

Nu het patroon duidelijk is op niveau van individuele bits, en aangezien we verder geen eisen gesteld hebben aan de h_i, is duidelijk dat de vier operatoren van het 2-splitsing universum een twee-onderscheidingen-structuur zullen opleggen aan een universum dat beschreven wordt door twee onderscheidingen en de vier h_i, die haakuitdrukkingen kunnen zijn, intensiteiten of intensiteiten van haakuitdrukkingen als eenheid.

Uiteraard zullen 2-splitsing operatoren ook in staat zijn operaties uit te voeren zonder het universum te verlaten. We gebruiken hier als voorbeeld:

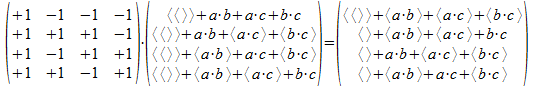
Deze operatie voert een transformatie uit van een orthogonale basis

Naar een basis waarvan de componenten niet orthogonaal zijn

Dit is terug een operatie die verschillende punten van de tralies opgespannen door de (orthogonale) projectoren (de componenten van de basis) in kolomformaat afbeelden op één punt als kolom. De kolomvector waarvan de componenten welgevormde haakvectoren zijn kan dus gezien worden als een som van getransformeerde kolommen.