Om de Hadamard transformatie te vinden met twee onderscheidingen kunnen we het tensorproduct nemen van twee Hadamard transformaties met een onderscheiding.

In het kort:

H₂⊗H₂=H₄

We passen H₄ toe op een kolom vector met vier componenten.

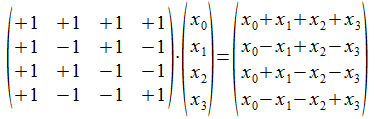
We tonen nu aan dat, onder de veronderstelling dat we als de vier componenten de basisvectoren van het twee-onderscheidingen universum nemen (allemaal welgevormde haakvectoren), we door deze transformatie over gaan van een vector in de basis {<>, a, b, a•b} naar een vector in de basis {<<a><b>>, <a<b>>, <<a>b>, <ab>} en omgekeerd.

Inderdaad is de volgende tabel gemakkelijk te construeren waarbij we van een vector in de basis {<<a><b>>, <a<b>>, <<a>b>, <ab>} naar een vector in de basis {<>, a, b, a•b} gaan en omgekeerd:

Dit zijn allemaal modulo3 sommen.

Wil men gewone sommen gebruiken dan moet men voor de inverse transformatie een normalisatie uitvoeren.

We zien hier duidelijker wat de actie is van een Hadamard matrix: welgevormde basisvectoren worden met elkaar gecombineerd tot de atomen van een universum, dus die welgevormde haakelementen die de maximale combinaties zijn van de basisvectoren. Ook omgekeerd geldt dit: uitgaande van de maximale elementen van een universum, namelijk degene die elkaar uitsluiten en dus de andere die altijd ervaren zijn “extraheert” men de basisvectoren.

Dit is zo voor even universa, bij een oneven universum (bijvoorbeeld met één-onderscheiding, of met drie onderscheidingen) bereikt men altijd de gecollapste atomen, dus de vectoren die maar één signatuurbit hebben.