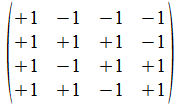We bestuderen operaties van het 2-splitsing universum nu op algemeen niveau met behulp van de matrix representatie. Meer specifiek willen we de relatie leggen met het creatief product voor toevoeging van meer dan één onderscheiding. We zullen aantonen dat de operaties van het 2-splitsing universum het mogelijk maken om gelijk welke structuur in functie van twee vrij gekozen onderscheidingen als standpunten te interpreteren.

Algemene operaties in het 2 splitsing universum kunnen gevormd worden door sommen te nemen van de basis operatoren in het 2 splitsing universum. De cellen in de 4x4 operatoren zullen we beschouwen als de signatuur string codering van het twee onderscheidingen universum op een analoge manier als we introduceerden bij het één onderscheiding universum. Signatuur strings zullen we dus kunnen herkennen in de rijen, maar ook in de kolommen. We zullen spreken van vier signatuur strings als rijbasis en vier signatuur strings als kolombasis. Deze begrippen worden verder uit de doeken gedaan. De rijbasis en de kolombasis zijn goed gekend vanuit de lineaire algebra.

We geven eerst een aantal toepassingen van operaties op kolomvectoren, dus een 2-splitsing voorgesteld als (h₁, h₂, h₃, h₄)^T, zodanig dat we hiermee een concrete manier kunnen introduceren om over die operaties te communiceren.

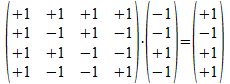
Veronderstel de operator 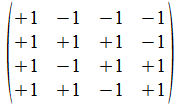die we de naam O geven.

De inwerking van de operator O op een kolomvector is de matrix vermenigvuldiging met de kolomvector rechts van de operator.

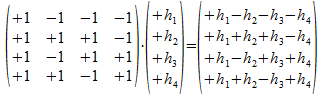
Het resultaat is dan een kolomvector en die vector interpreteren we dan als een som van vectorvermenigvuldigingen met punten uit het twee onderscheidingen universum dat we conventioneel opspannen met a en b (en waarvoor we een willekeurige leesrichting kiezen in de bitstring). De interpretatie geven we aan door het teken ∼ te gebruiken:

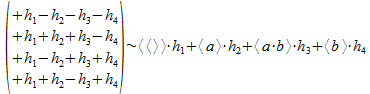
Deze operator O gaat dus een willekeurig punt h uit het 2-splitsing universum (h die in een niet nader gespecificeerd universum uitgedrukt is en die hier voorgesteld is als kolommatrix (h₁, h₂, h₃, h₄)^T) omzetten in een ander punt waarvan de componenten gevormd zijn door de vector vermenigvuldiging (het “dot product”) van een component van de kolommatrix met het punt gecodeerd in de rijen van de operator O (dit zijn voor deze operator 3 AND atomen en 1 OR atoom, namelijk (+---); (+++-); (+-++); (++-+)).

De kolommatrix die zo ontstaat kunnen we nu interpreteren als de som van de projectie van de componenten h_i (die verder niet gekend moeten zijn) op het punt gecodeerd in de kolommen van de operator O (dit zijn voor deze operator de basisvectoren (++++); (-+-+); (-++-); (--++)) en die dus wel gekend zijn en conventioneel gekozen worden. We geven deze kolomvectoren de conventionele naam die we kennen van het twee-onderscheidingen universum.

De inverse operator O^-1 zal deze transformatie in de inverse richting uitvoeren, noteer dat alle sommen modulo 3 sommen zijn. Het is duidelijk te zien dat de inverse operator van dit voorbeeld niet te onderscheiden is van de transpose van de operator en de operator een 2π-rotatie operator is.

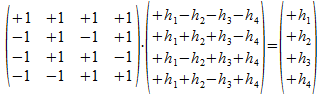
Als we de vier AND-atomen van het twee-onderscheidingen universum nu de namen geven A₁, A₂, A₃, A₄, en de vier OR-atomen de namen O₁, O₂, O₃, O₄, dan zal de inverse of transpose van de operator O een variant van de atoombasis construeren die gevormd wordt door drie AND-atomen en één OR-atoom:

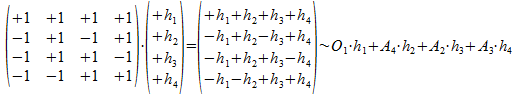
We hebben helemaal niets verondersteld over de h_i, en alle veronderstellingen zijn nog open. Bijvoorbeeld: als de h_i onderling orthogonaal zijn (en dus gecollapste punten zijn) zijn de h_i te interpreteren als punten (die een som zijn van basisvectoren van een eigen universum) die een directe som van gecollapste tralies vormen en dus eveneens basisvectoren zijn maar van het gecollapste type.

We kunnen zelfs zeer willekeurige interpretaties kiezen, de kolomvector (h₁, h₂, h₃, h₄)^T kunnen we als volgt interpreteren:

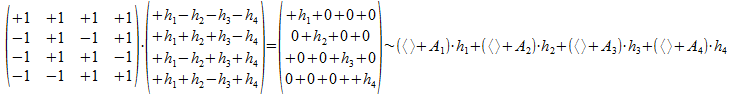
Dit maakt overduidelijk dat de voorstelling zeer arbitrair is met gecollapste atomen, of punten die vermenigvuldigd met elkaar de al-nul vector opleveren.

Enkele speciale gevallen

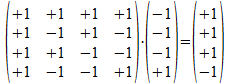
De interpretatie als kolomvectoren (en rijvectoren) die een codering zijn van het twee onderscheidingen universum verantwoorden we doordat de basis kolomvectoren gevormd worden door de basisoperatoren te laten inwerken op de kolommatrix (<<>> <<>> <<>> <<>>)^T. Bijvoorbeeld:

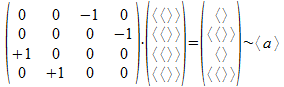
Met een ander voorbeeld zal de operator met drie AND-atomen en een OR-atoom als rijbasis en de vier basisvectoren als kolombasis door inwerking op de kolomvector met voor alle h_i de welgevormde haakuitdrukking <<>> (anders genoteerd als +1) deze kolomvector transformeren in een kolomvector die we interpreteren als de signatuur string van de welgevormde haakuitdrukking ab of <a><b>, afhankelijk van de richting waarin we de kolomvector willen lezen.

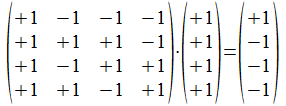
Merk op dat de som van de basisvectoren die in de kolombasis gebruikt worden overeenkomt met ab: <<>>⊕<a>⊕<a•b>⊕<b>. De matrixvermenigvuldiging met de kolomvector <<>> in modulo3 interpretatie komt dan overeen met de transformatie (ab)•<<>>, maar die interpretatie zal enkel gelden bij vermenigvuldiging met <<>> aangezien de matrixvermenigvuldiging niet commutatief is en het vectorproduct (inbedding van de transformatie) wel commutatief is.

Met nog een ander voorbeeld zullen operatoren met basisvectoren als rijbasis en kolombasis (Hadamard operatoren) atomen transformeren in elkaar.