Meer dan die twee soorten getallen hebben we niet nodig om de potentiële werkelijkheid dank zij materiële sporen op te spannen: een getal dat een gesloten geheel kan modelleren, dus iets dat niet verandert, dus iets dat door een beperkt aantal onderscheidingen kan beschreven worden en een getal dat iets kan modelleren dat altijd groter (kleiner) kan worden en dus onvermijdelijk altijd verandert en niet door een beperkt aantal onderscheidingen beschreven kan worden.
Het ene getal kunnen we verbinden aan het begrip “entiteit” of “eenheid” en het andere aan het begrip “intensiteit” of “veelheid”.
We kunnen in eη+iθ de fase θ als invariant te kiezen (bijvoorbeeld gelijk aan nul te nemen of gelijk welke fractie van π, fractie die dan invariant is). Dan modelleren we geen golf, geen trilling, wat we modelleren “is in fase”. Het complex getal geeft dan de intensiteit van een waargenomen punt op een bepaalde diepte in de (impliciet gekozen) tralie in de ervaren situatie en dus in een gecollapste tralie. Het verband tussen η en n of m kunnen we dan kwalitatief onderzoeken. Veronderstel enerzijds dat n vast is en dat m varieert, als n een macht is van 2 kan n dus staan voor een aantal atomen. De exponent η is ln(n) voor m=0 en neemt af bij toenemende m tot hij 0 is voor m=n.

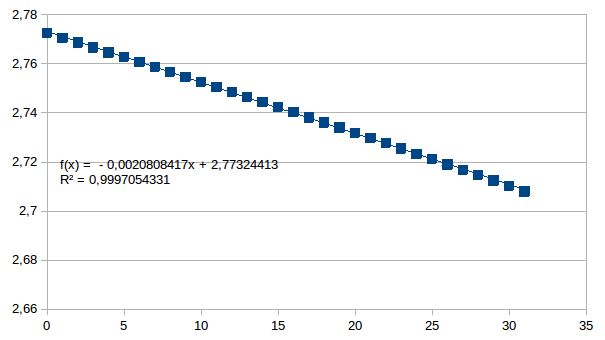
Hoe groter n is hoe meer het verband tussen η en m lineair is. De onderstaande grafiek geeft het nagenoeg lineair verband voor m van 0 tot 31 voor een vaste n=256=28 (de best passende formule is op de grafiek weergegeven met de determinatiecoëfficiënt R2, hierin is x de variabele m).
Veronderstel
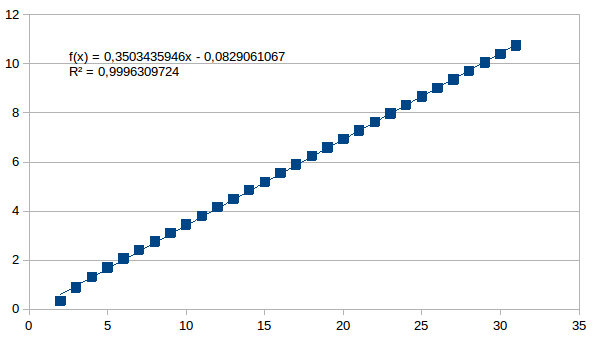
anderzijds dat m vast is, n varieert als macht van 2. Een bepaalde m
is slechts vanaf een bepaald universum mogelijk (n moet altijd groter
zijn dan m) en ook hier zien we een nagenoeg lineair verband.
Het waargenomen punt is te interpreteren als een eenheid (het complex getal eiθ) met een intensiteit (n-m)1/2. De intensiteit is een afstand in de tralie, wat te zien is door het verband met de cartesiaanse vorm x=rcosθ en y=rsinθ met r = (x2+y2)1/2.
Dit inzicht is ook een illustratie van een beperking die geldt voor elk soort empirisch onderzoek en dus voor kennis die opgebouwd wordt als inductie vanuit de eigen waarnemingen van een agens. Zoals in de grafiek duidelijk wordt, zou het agens de hypothese van een lineair verband (een determinatiecoëfficiënt zo goed als gelijk aan 1) als een gegronde hypothese kunnen beoordelen. En inderdaad zou het agens hiermee anticipaties kunnen bedenken die terug empirisch kunnen getoetst worden. Een standpunt dat voldoende verwijderd is van het lokaal zicht zou best niet bereikbaar kunnen zijn voor empirisch onderzoek op basis waarvan het agens zou moeten besluiten tot een exponentieel verband. Hierdoor zou het agens de relaties niet kunnen inschatten die zijn eigen beperkingen hebben met andere mogelijkheden en beperkingen die misschien door andere agentia wel bereikbaar zijn. Dit is enkel vanuit creativiteit en dus theoretische abstractie te construeren en dan ook te waarderen en dit onderstreept dus ook het blijvend belang van verbeelding voor een agens: er zal ook altijd iets anders gebeuren dan datgene dat het agens doet gebeuren.
In (n-m)1/2eiθ zouden we ook n-m gelijk aan 1 kunnen nemen. Dit maakt de eenheid duidelijk die als intensiteit eiθ krijgt: het is een atoom. Alle ervaren punten op de diepte m=n-1 kunnen door hetzelfde getal 1=(n-m)1/2 gekarakteriseerd worden, in bitstring hebben die punten allemaal n-1 bits met dezelfde waarde, zo we willen kunnen we ze beschouwen als don’t cares of onbetekende bits. Al die punten kunnen dan alle mogelijk intensiteiten eiθ krijgen en wat we dan modelleren is een soort trilling, een “kwantumgedrag”. Dat gedrag is enkel probabilistisch te beschrijven en leidt tot een mogelijke verwachting van waarneming, verwachting die slechts na de waarneming kan gecontroleerd worden als de toestand (atoom) waarin de werkelijkheid zich na de waarneming bevindt. Merk op dat atomen geen entiteiten zijn (atomen zijn niet telbaar).
De “diepte m” (het niveauverschil) is een metrische maat. Aangezien we n en m vrij kunnen kiezen kunnen we ook de meest eenvoudige situatie nemen: n gelijk 2 en m gelijk 0 en dus n-m=2, waarbij we een één-onderscheiding universum kiezen. De intensiteit eiθ kan daarom beschouwd worden als de coëfficiënt van een punt dat niet kan onderscheiden worden van <> (het ervaren standpunt, wat gekozen wordt) of <<>> (het gebeurde, wat niet gekozen wordt), en voor andere universa met n-m=2 is dat dan de genormaliseerde (want (n-m)1/2 is 21/2) trilling van een telbare entiteit.
Noteer dat als m gelijk aan n genomen wordt men zou kunnen redeneren dat een hoek niet gedefinieerd kan worden aangezien de noemer, van bijvoorbeeld cosθ = ±(n-m-p)1/2(n-m)-1/2 of sinθ = ±p1/2(n-m)-1/2, dan niet verschillend is van nul. Nochtans kunnen we de verhouding van beide berekenen en dus tanθ = ±w<>1/4w-1/4=±p1/2(n-m-p)-1/2=±1 en de hoek is dus π/4.
We kunnen nog andere interpretaties voor complexe getallen onderzoeken. Welk welgevormd punt kan bijvoorbeeld als intensiteit het getal 1+i hebben? Er geldt 1+i=21/2eiπ/4 en met 1 = x = ±(n-m-p)1/2(n-m)-1/2 en 1 = y = ±p1/2(n-m)-1/2 kunnen we afleiden dat dit geldt ofwel voor p=0, ofwel voor p=n-m.
Het getal x+iy kan dus geïnterpreteerd worden als de coëfficiënt van de ervaren standpunt-vector in het gekozen universum op een diepte m in de tralie. De extremen zijn p=0 en p=n-m.
Voorbeeld voor θ=±π of θ=0 en dus p=0
cosθ = ±(n-m-p)1/2(n-m)-1/2 = ±(-1)
sinθ = ±p1/2(n-m)-1/2 = 0
Voorbeeld voor θ=±π/2 en dus p=n-m
cosθ = ±(n-m-p)1/2(n-m)-1/2 = 0
sinθ = ±p1/2(n-m)-1/2 = ±1
Het eerste geval betekent dat er enkel maar gemeenschappelijke punten zijn, er zijn geen twee categorieën van waarnemingen, ofwel zijn alle waarnemingen “ja”, ofwel zijn ze “neen” en dat is een volledig evenwaardige situatie. Er is dus stabiliteit. Ondanks het feit dat elke waarneming een andere uitsluit krijgt elke waarneming dezelfde waardering: een van de twee extrema van gelijk welke tralie, <> ofwel <<>>. Dus θ=±π of θ=0 is niet anders dan het centraal axioma: ervaren is onvermijdelijk.
Het tweede geval betekent dat p en n-m even groot zijn, dus de totale bitstring is het dubbele van de bitstring die de gemeenschappelijke bits geeft. Het kan dus niet anders dan dat het vectorproduct van de twee categorieën van de waarneming een centraal punt is in een universum met één toegevoegde onderscheiding (het vectorproduct zal aan de gemeenschappelijke een bepaalde waardering geven en de complementaire waardering aan het even grote aantal van niet gemeenschappelijke). Dit is dus de andere grens van het model. Dus θ=±π/2 is niet anders dan het centraal axioma: er gebeurt ook altijd iets anders (en dat kan dan als een nieuwe onderscheiding genomen worden).
Dit demonstreert ook duidelijk dat de hoek θ de diepte geeft tussen een extremum (eerste geval) en het centraal niveau (tweede geval) in de gecollapste tralie. We kunnen daarom het volgende beeld construeren dat isomorf is met een eenheidsvector die een cirkel in dezelfde zin, neem tegenwijzerzin, doorloopt: start bij 0 en neem dit als overeenkomst met een extremum van de tralie. Bij toenemende θ wordt +π/2 bereikt als de tralie van dat extremum naar centraal niveau doorlopen wordt en er één punt per niveau gemodelleerd wordt. Bij toenemende θ wordt +π bereikt als in de tralie het andere extremum bereikt wordt. Bij toenemende θ wordt dan -π/2 bereikt als in de tralie vanuit het tweede extremum stap voor stap terug het centraal niveau bereikt wordt. Bij toenemende θ wordt dan 0 bereikt en het extremum dat bij de start gekozen werd
Vandaar dat we de modulaire opbouw van het haakformalisme ook kunnen uitvoeren met de getallen 1+i versus -1-i.
De som die aan de basis ligt van de constructie van de getallen functioneert zowel als de gemeten entiteiten een relatie hebben met elkaar (en dus elkaar “door trilling” beïnvloeden) en dus als een relatie gemeten worden (in één tralie) of als de gemeten entiteiten geen relatie hebben met elkaar en dus als een som van meerdere (deel)tralies gemeten worden, tralies die elkaar uitsluiten. Toch blijft de begrenzing van n essentieel en dat kunnen we interpreteren als energie (de (on)mogelijkheid tot gedrag) of massa (de (on)mogelijkheid tot gedrag).