Divergeren en convergeren

Door het onderzoek naar de transformaties tussen atoom patronen is het mogelijk om te bestuderen wat de relatie is van universa tot elkaar die deels met dezelfde onderscheidingen opgespannen worden. Die onderscheidingen moeten daarenboven niet a priori gekend worden, de communicerende agentia (bijvoorbeeld ontwerper en stakeholder) kunnen op zoek gaan naar aspecten die enkel kunnen blijken te gebeuren in het grootste universum dat voor hen samen bereikbaar is. Ontwerpen en communiceren kunnen en zullen we daarom operationeel niet onderscheiden.

Met het meest eenvoudige voorbeeld herhalen we nog eens de essentie van het inzicht. De transformatie a↔ab kan niet onderscheiden worden van a↔<>. Dit betekent dat beide een “indien... dan... zo niet...” constructie representeren in een universum van twee onderscheidingen die een waarde toegekend krijgt. De dubbele pijl interpreteren we in het onderzoek naar de transformatie tussen atoompatronen als één voorstelling van twee morfismen: bij het divergeren zullen we het universum met minder onderscheidingen (dus a) als domein van een deelmorfisme (DOM) nemen en het grotere universum (dus ab) als codomein van het deelmorfisme (COD). In het grotere universum wordt dus b als nevenschikking toegevoegd aan a. De omgekeerde richting modelleert het convergeren. Dus: als we schrijven a↔ab dan is de pijl naar rechts divergeren (naar een groter repertorium of domein) en naar links convergeren (naar een kleiner repertorium of domein). Convergeren en divergeren zijn acties en dus dubbel op dezelfde manier als a↔<> dat is dat niet verschillend is van <a>↔<<>>. Het grotere universum kunnen we altijd laten gebeuren en dat is juist het testen dat zo'n fundamentele plaats inneemt in de toegepaste wetenschappen. Een test gebeurt altijd in het grootste universum. Dus: een transformatie tussen atoompatronen van een kleiner naar een groter universum dat het kleinere universum “impliceert”, en omgekeerd van een groter naar een kleiner universum is uit te drukken als een welgevormde haakuitdrukking die in het ervaren ofwel een inbedding is ofwel niet. Deze welgevormde haakuitdrukking is een uitdrukking in het grootste universum. Het is nu belangrijk om in te zien dat zowel convergeren en divergeren, evenzeer als het uitvoeren van een transformatie een actie is. In het ervaren worden de twee morfismen simultaan uitgevoerd. Dit betekent dus dat we de uitdrukking a↔ab een waarde geven, en aangezien a↔ab niet verschillend is van a↔<> geven we dus a een waarde, waarbij we dus a bijvoorbeeld kiezen te ervaren, dus formeel voeren we de collaps a↔<> uit, wat niet verschillend is van het laten gebeuren van de inbedding, formeel voeren we dan de collaps <a>↔<<>> uit. Maar we kunnen ook a laten gebeuren, dus formeel voeren we de collaps a↔<<>> uit, wat niet verschillend is van het ervaren van de inbedding, formeel voeren we dan de collaps <a>↔<> uit. Merk op dat we terug de dubbele pijl gebruiken.

Door de actie (convergentie versus divergentie uitvoeren) zal blijken wat de grenzen zijn van domein en codomein. De essentie van convergeren versus divergeren is: op zoek gaan in welk universum iets (ir)relevant wordt. Het is dan nodig om twee richtingen te checken (kiezen en laten gebeuren): a↔<> betekent: als b ervaren is moet ook a ervaren zijn maar ook: als a gebeurt moet ook b gebeuren. Maar dat is niet de enige interpretatie wat we duidelijk proberen te maken in de onderstaande tabel.

a↔<>

Als b ervaren is moet ook a ervaren zijn

en ook

Als a gebeurt moet ook b gebeuren of: als iets anders dan a ervaren wordt dan moet ook iets anders dan b ervaren worden

<<a>>↔<>

Als <a> ervaren is moet ook ervaren zijn of: als a gebeurt dan gebeurt b

en ook

Als gebeurt moet ook <a> gebeuren of: als iets anders dan ervaren wordt dan moet ook iets anders dan <a> ervaren worden

De reden voor deze dubbele interpretatie is dat we aan de gebruikte symbolen geen absolute betekenis geven. Als we a als symbool gebruiken dan kan dat betekenen dat we a positief waarderen: a is een begerenswaardige toestand, maar evenzeer zou dat kunnen dat we <a>, bijvoorbeeld het vermijden van a, een begerenswaardige toestand noemen. Dit is een essentieel inzicht als we de communicatie tussen stakeholders helder willen houden. Wat begerenswaardig is voor een agens A in toestand X, is misschien niet begerenswaardig voor een agens B in toestand X, maar wel begerenswaardig voor B in toestand Y. Met een voorbeeld: wat in de ene cultuur een deugd genoemd wordt en maximaal nagestreefd zal worden (bijvoorbeeld de vruchten van de natuur maximaal exploiteren), kan in een andere cultuur als te vermijden of zelfs als zeer verwerpelijk geïnterpreteerd worden.

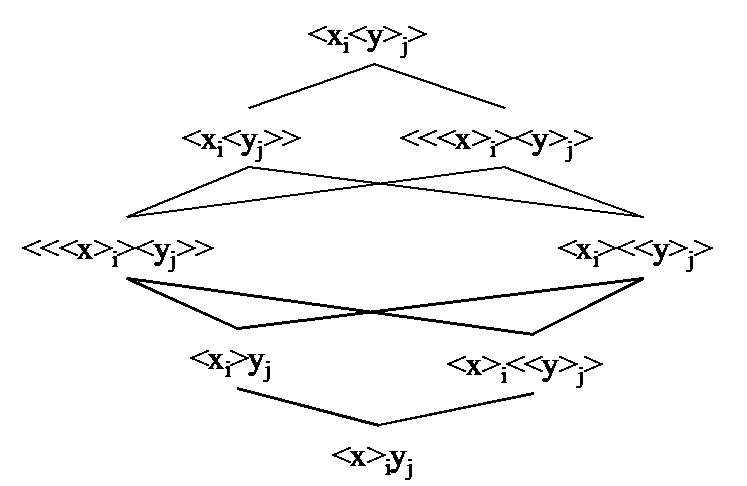
Hieronder geven we de volledige tabellen van de welgevormde haakuitdrukkingen en hun relatie met interpretaties wanneer we aan de uitdrukking een waarde toekennen. We maken hierbij nuttig gebruik van het onderzoek over de relaties tussen deelverzamelingen. De mogelijke relaties deelverzameling/verschilverzameling vormen 4 tralies die in elkaar kunnen getransformeerd worden. Deze vier tralies representeren dus maar één patroon als men rekening houdt met het zojuist gegeven voorbeeld dat symbolen geen absolute betekenis hebben. Om dit te beklemtonen geven we de tralies de naam “verschillend” en “gelijkaardig” (met hun inbeddingen). We geven de tralie zowel grafisch als in tabel vorm en vullen de tabelvorm aan met de overeenkomstige transformatie van divergentie/convergentie. De focus ligt op het universum waarnaar geconvergeerd zou kunnen worden: het universum opgespannen door de y symbolen. De x symbolen zijn toegevoegde symbolen waarnaar gedivergeerd zou kunnen worden door ze op te nemen bij de y symbolen. Dus als men de conventie zou willen aannemen dat een symbool zonder haken als begerenswaardig, positief, gewild, ... geïnterpreteerd moet worden dan zou men een opsplitsing kunnen maken als volgt: x_i met i van 1 tot n kan geïnterpreteerd worden als x_i met i van 1 tot k als x_i en als <x>_i met i van k+1 tot n, en y_j met j van 1 tot m kan geïnterpreteerd worden als y_j met j van 1 tot l als y_j en als <y>_j met j van l+1 tot m.

Om het contrast aan te geven met de klassieke predicaten logica is bij een aantal welgevormde haakuitdrukkingen de overeenkomstige predicaten interpretatie aangegeven. Dit is voornamelijk om te illustreren hoe slecht uitspraken in de standaard taal in staat zijn om de operationeel onderbouwde relaties tussen welgevormde haakuitdrukkingen uit te drukken.

Verschillend

In tabelvorm:

<x_i<y>_j>↔<>	∃x, ∀y, y∉x en ook ∀<x>, ∃<y>, <x>∉<y>	<<y>_j>↔<x_i><y>_j	Als alle y ervaren zijn dan moeten alle x gebeuren Het is onmogelijk dat sommige y gebeuren, dat sommige y te mijden zijn
<x_i<y_j>>↔<>	∀<x>, ∀<y>, <x>∉<y> en ook ∃x, ∃y, y∉x	y_j↔<x_i><y_j>	Als sommige y ervaren zijn dan moeten alle x gebeuren Het is onmogelijk dat alle y gebeuren	<<<x>_i><y>_j>↔<>	∀x, ∀y, y∉x en ook ∃<x>, ∃<y>, <x>∉<y>	<<y>_j>↔<x>_i<y>_j	Als alle y ervaren zijn dan moeten sommige x gebeuren Het is onmogelijk dat sommige y gebeuren
<<<x>_i><y_j>>↔<>	∀x, ∃y, y∉x en ook ∃<x>, ∀<y>, <x>∉<y>	y_j↔<x>_i<y_j>	Als sommige y ervaren zijn dan moeten sommige x gebeuren Het is onmogelijk dat alle y gebeuren	<x_i><<y>_j>↔<>	Sommige x zijn alle y ∀<x>, ∃<y>, <y>∈<x> en ook ∃x, ∀y, x∈y	<<y>_j>↔x_i<<y>_j>	Als alle y ervaren zijn dan is de waarde van x irrelevant Als sommige y gebeuren dan moeten alle x gebeuren
<x_i>y_j↔<>	Sommige x impliceren sommige y ∀<x>, ∀<y>, <y>∈<x> en ook ∃x, ∃y, x∈y	y_j↔x_iy_j	Als sommige y ervaren zijn dan is de waarde van x irrelevant Als alle y gebeuren dan moeten alle x gebeuren	<x>_i<<y>_j>↔<>	Alle x zijn alle y ∀x, ∀y, x∈y en ook ∃<x>, ∃<y>, <y>∈<x>	<<y>_j>↔<<x>_i><<y>_j>	Als alle y ervaren ijn dan is de waarde van x irrelevant Als sommige y gebeuren dan moeten sommige x gebeuren
<x>_iy_j↔<>	Alle x impliceren sommige y ∃<x>, ∀<y>, <y>∈<x> en ook ∀x, ∃y, x∈y	y_j↔<<x>_i>y_j	Als sommige y ervaren zijn dan is de waarde van x irrelevant Als alle y gebeuren dan moeten sommige x gebeuren

<Verschillend>

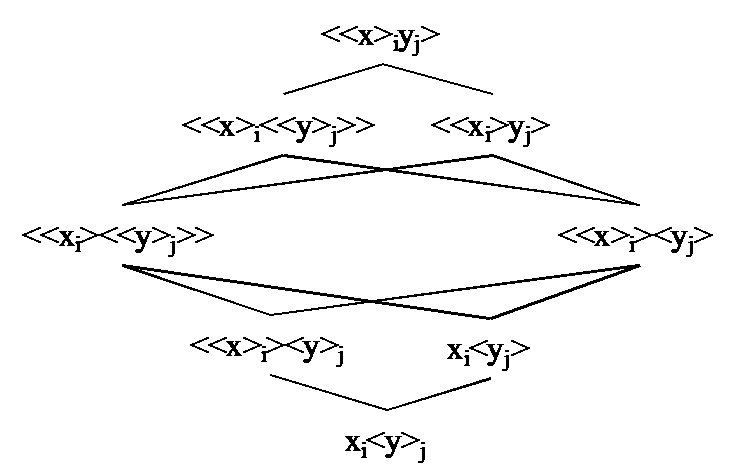
In tabelvorm:

<<x>_iy_j>↔<>

∀x, ∃y, x∉y

en ook

∃<x>, ∀<y>, <y>∉<x>

<y_j>↔<<x>_i>y_j

en ook

y_j↔<<<x>_i>y_j>

Het is onmogelijk dat sommige y ervaren zijn

Als alle y gebeuren dan moeten alle x ervaren zijn

<<x>_i<<y>_j>>↔<>

Het is niet zo dat alle x alle y zijn

∀x, ∀y, x∉y

en ook

∃<x>, ∃<y>, <y>∉<x>

en ook

<<y>_j>↔<<<x>_i><<y>_j>>

Het is onmogelijk dat alle y ervaren zijn

Als sommige y gebeuren dan moeten alle x ervaren zijn

<<x_i>y_j>↔<>

Sommige x zijn anders dan sommige y

∀<x>, ∀<y>, <y>∉<x>

en ook

∃x, ∃y, x∉y

<y_j>↔x_iy_j

en ook

y_j↔<x_iy_j>

Het is onmogelijk dat sommige y ervaren zijn

Als alle y gebeuren dan moeten sommige x ervaren zijn

<<x_i><<y>_j>>↔<>

∃x, ∀y, x∉y

en ook

∀<x>, ∃<y>, <y>∉<x>

en ook

<<y>_j>↔<x_i<<y>_j>>

Het is onmogelijk dat alle y ervaren zijn

Als sommige y gebeuren dan moeten sommige x ervaren zijn

<<x>_i><y_j>↔<>

Sommige y zijn alle x

∀x, ∃y, y∈x

en ook

∃<x>, ∀<y>, <x>∈<y>

<y_j>↔<x>_i<y_j>

en ook

y_j↔<<x>_i<y_j>>

Als sommige y ervaren zijn dan moeten alle x ervaren zijn

Als alle y gebeuren dan is de waarde van x irrelevant

<<x>_i><y>_j↔<>

Alle y zijn alle x

∀x, ∀y, y∈x

en ook

∃<x>, ∃<y>, <x>∈<y>

<y>_j↔<x>_i<y>_j

en ook

<<y>_j>↔<<x>_i<y>_j>

Als alle y ervaren zijn dan moeten alle x ervaren zijn

Als sommige y gebeuren dan is de waarde van x irrelevant

x_i<y_j>↔<>

Sommige y zijn sommige x

∀<x>, ∀<y>, <x>∈<y>

en ook

∃x, ∃y, y∈x

<y_j>↔<x_i><y_j>

en ook

y_j↔<<x_i><y_j>>

Als sommige y ervaren zijn dan moeten sommige x ervaren zijn

Als alle y gebeuren dan is de waarde van x irrelevant

x_i<y>_j↔<>

Alle y zijn sommige x

∀<x>, ∃<y>, <x>∈<y>

en ook

∃x, ∀y, y∈x

<y>_j↔<x_i><y>_j

en ook

<<y>_j>↔<<x_i><y>_j>

Als alle y ervaren zijn dan moeten sommige x ervaren zijn

Als sommige y gebeuren dan is de waarde van x irrelevant

Gelijkaardig

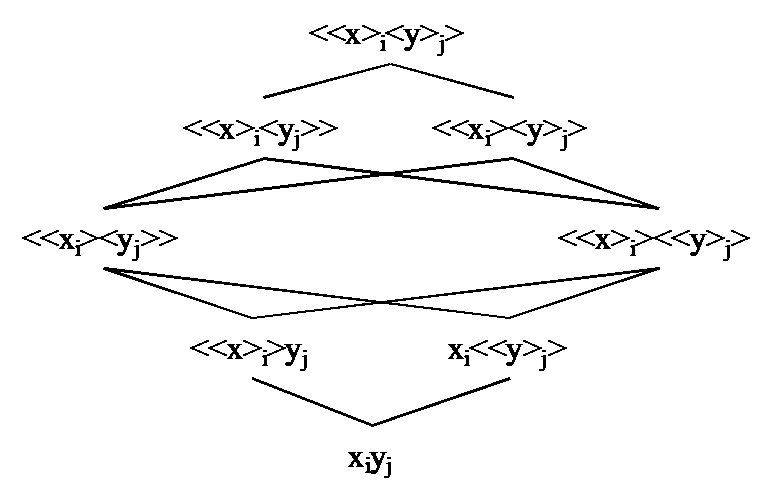
In tabelvorm:

<<x>_i<y>_j>↔<>	De existentie van alle x en alle y ∀x, ∃<y>, x∉<y> en ook ∃<x>, ∀y, y∉<x>	<<y>_j>↔<<x>_i><y>_j en ook <<x>_i>↔<<y>_j><x>_i	Als alle y ervaren zijn dan moeten alle x ervaren zijn Het is onmogelijk dat sommige y gebeuren En vice versa
<<x>_i<y_j>>↔<>	∃<x>, ∃y, y∉<x> en ook ∀x, ∀<y>, x∉<y>	y_j↔<<x>_i><y_j>	Als sommige y ervaren zijn dan moeten alle x ervaren zijn Het is onmogelijk dat alle y gebeuren	<<x_i><y>_j>↔<>	∃x, ∃<y>, x∉<y> en ook ∀<x>, ∀y, y∉<x>	<<y>_j>↔x_i<y>_j	Als alle y ervaren zijn dan moeten sommige x ervaren zijn Het is onmogelijk dat sommige y gebeuren
<<x_i><y_j>>↔<>	De existentie van een x en een y ∃x, ∀<y>, x∉<y> en ook ∀<x>, ∃y, y∉<x>	y_j↔x_i<y_j> en ook x_i↔y_j<x_i>	Als sommige y ervaren zijn dan moeten sommige x ervaren zijn Het is onmogelijk dat alle y gebeuren en vice versa	<<x>_i><<y>_j>↔<>	De existentie van alle x of alle y ∃<x>, ∀y, <x>∈y en ook ∀x, ∃<y>, <y>∈x	<<y>_j>↔<x>_i<<y>_j> en ook <<x>_i>↔<y>_j<<x>_i>	Als alle y ervaren zijn dan is de waarde van x irrelevant Als sommige y gebeuren dan moeten sommige x gebeuren en vice versa
<<x>_i>y_j↔<>	∃<x>, ∃y, <x>∈y en ook ∀x, ∀<y>, <y>∈x	y_j↔<x>_iy_j	Als sommige y ervaren zijn dan is de waarde van x irrelevant Als alle y gebeuren dan moeten alle x ervaren zijn	x_i<<y>_j>↔<>	∃x, ∃<y>, <y>∈x en ook ∀<x>, ∀y, <x>∈y	<<y>_j>↔<x_i><<y>_j>	Als al y ervaren zijn dan is de waarde van x irrelevant Als sommige y gebeuren dan moeten sommige x ervaren zijn
x_iy_j↔<>	De existentie van een x of een y ∃x, ∀<y>, <y>∈x en ook ∀<x>, ∃y, <x>∈y	y_j↔<x_i>y_j en ook x_i↔<y_j>x_i	Als sommige y ervaren zijn dan is de waarde van x irrelevant Als alle y gebeuren dan moeten sommige x ervaren zijn en vice versa

<Gelijkaardig>

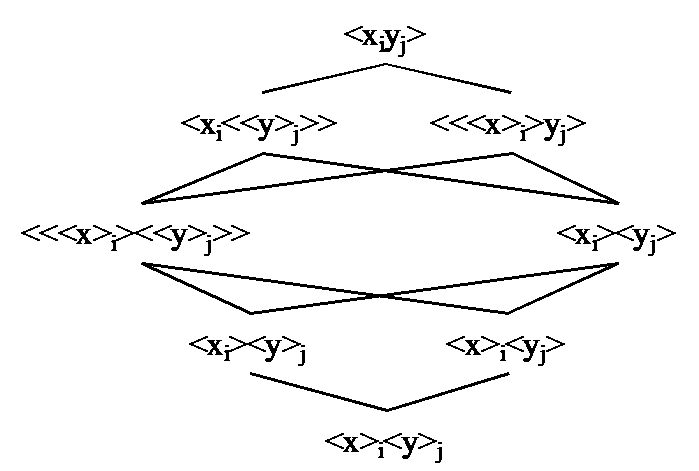
In tabelvorm:

<x_iy_j>↔<>

De existentie van alle <x> en alle <y>

∀<x>, ∃y, <x>∉y

en ook

∃x, ∀<y>, <y>∉x

<y_j>↔<x_i>y_j

y_j↔<<x_i>y_j>

en ook

<x_i>↔<y_j>x_i

x_i↔<<y_j>x_i>

Het is onmogelijk sommige y te ervaren

Als alle y gebeuren dan moeten alle x gebeuren

en vice versa

<x_i<<y>_j>>↔<>

∃x, ∃<y>, <y>∉x

en ook

∀<x>, ∀y, <x>∉y

y_j↔<<x_i><<y>_j>>

Het is onmogelijk sommige y te ervaren

Als alle y gebeuren dan moeten alle x gebeuren

<<<x>_i>y_j>↔<>

∃<x>, ∃y, <x>∉y

en ook

∀x, ∀<y>, <y>∉x

<y_j>↔<x>_iy_j

y_j↔<<x>_iy_j>

Het is onmogelijk sommige y te ervaren

Als alle y gebeuren dan moeten sommige x gebeuren

<<<x>_i><<y>_j>>↔<>

De existentie van een <x> en een <y>

∃<x>, ∀y, <x>∉y

en ook

∀x, ∃<y>, <y>∉x

<<y>_j>↔<<x>_i<<y>_j>>

en ook

<<x>_i>↔<<y>_j<<x>_i>>

Het is onmogelijk alle y te ervaren

Als sommige y gebeuren dan moeten sommige x gebeuren

en vice versa

<x_i><y_j>↔<>

De existentie van alle <x> of alle <y>

∃x, ∀<y>, x∈<y>

en ook

∀<x>, ∃y, y∈<x>

<y_j>↔x_i<y_j>

y_j↔<x_i<y_j>>

en ook

<x_i>↔y_j<x_i>

x_i↔<y_j<x_i>>

Als sommige y ervaren zijn dan moeten alle x gebeuren

Als alle y gebeuren dan is de waarde van x irrelevant

en vice versa

<x_i><y>_j↔<>

∃x, ∃<y>, x∈<y>

en ook

∀<x>, ∀y, y∈<x>

<y>_j↔x_i<y>_j

<<y>_j>↔<x_i<y>_j>

Als alle y ervaren zijn dan moeten alle x gebeuren

Als sommige y gebeuren dan is de waarde van x irrelevant

∃<x>, ∃y, y∈<x>

en ook

∀x, ∀<y>, x∈<y>

<y_j>↔<<x>_i><y_j>

y_j↔<<<x>_i><y_j>>

Als sommige y ervaren zijn dan moeten sommige x gebeuren

Als alle y gebeuren dan is de waarde van x irrelevant

De existentie van een <x> of een <y>

∃<x>, ∀y, y∈<x>

en ook

∀x, ∃<y>, x∈<y>

<y>_j↔<<x>_i><y>_j

<<y>_j>↔<<<x>_i><y>_j>

en ook

<x>_i↔<<y>_j><x>_i

<<x>_i>↔<<<y>_j><x>_i>

Als alle y ervaren zijn dan moeten sommige x gebeuren

Als sommige y gebeuren dan is de waarde van x irrelevant

en vice versa