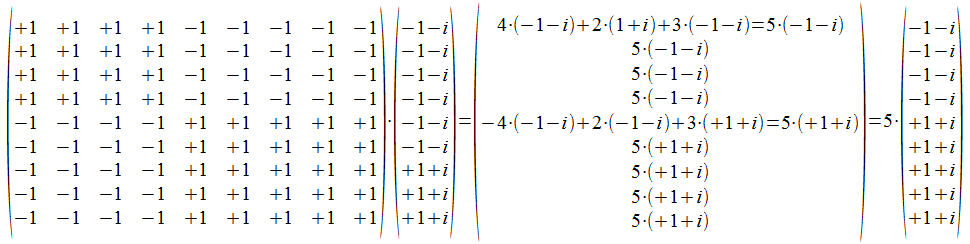
We werken nu een voorbeeld uit in het operator formalisme door toepassing van de daar gedefinieerde projectoren. Een projector is het aanwezen instrument omdat hij geen onderscheid maakt tussen punten en hun inbedding, dus AND-atomen en hun inbeddingen de OR-atomen.
We kiezen voor het voorbeeld een bitstring met 9 componenten. Merk op dat het aantal bits vrij kan gekozen worden, dat de volgorde van de bits onbelangrijk is en ook of het nu hoog- of laag-bits zijn. Willen de gekozen punten echter in onderscheidingen geïnterpreteerd kunnen worden, dan zullen zowel het totaal aantal n als de volgorde van de bits een doorslaggevende rol spelen. Elke n die afwijkt van 2EXP2q kan altijd met don't care x aangevuld worden tot een groter getal bereikt wordt dat wel gelijk is aan 2EXP2q. Dit is in wezen niets anders dan dat men het eerst volgende onderscheidingen universum beschouwt als tralie waarin een deeltralie reeds een ervaringswaarde heeft.
De getallen die we in het model kunnen berekenen zijn gerelateerd aan de aantallen die gemeten worden. In het projector formalisme speelt hierbij het inwendig product een centrale rol, dus ook het niveauverschil in de tralie. We zullen ook de hiervan afgeleide vorm (het getal g of w) gebruiken die vanuit een operator berekend wordt. Dit getal zullen we een gewicht noemen, zoals het ook in de kwantummechanica genoemd wordt waar dit de vorm <xp|Pq|xp> krijgt. We doen dat zowel voor potentiële punten als voor ervaren punten en we tonen aan dat enkel in het ervaren zelf effectief een aantal atomen geteld wordt.
Het punt dat als gemeenschappelijk punt zal fungeren kiezen we als 111000000, en het zou tot 111000000xxxxxxx kunnen uitgebreid worden om op een onderscheidingen universum afgebeeld te kunnen worden. Merk op dat dit in de berekeningen niets zal veranderen.
Dat maakt duidelijk dat m=3 gegeven is en dat we nu kiezen voor p=2, dus n-m-p=4.
Het aantal bits gelijk met het gemeenschappelijk punt: 3+4=m+(n-m-p)
Het aantal bits verschillend: 2=n-(m+(n-m-p))=p
Het aantal gelijk min het aantal verschillend: 3+4-2=5=m+n-m-p-n+m+n-m-p=n-2p
Het gemeenschappelijk punt 111000000 projecteren we eerst in de ruimte van M<>, namelijk 1111100000.
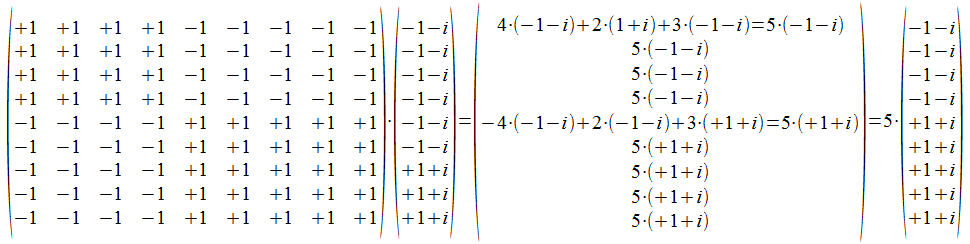
We berekenen nu het inwendig product van het gemeenschappelijk punt met de resultaat vector
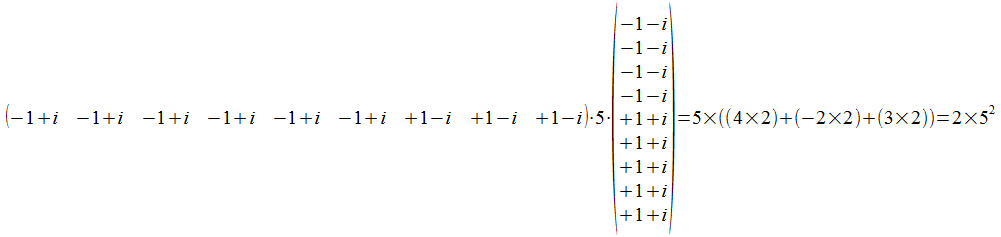
Inderdaad: het gewicht van M<> of (m1)(p1)000... is 2(n-2p)2 en in dit concrete geval 2×52.
Het aantal bits gelijk met het gemeenschappelijk punt: 3+2=m+p
Het aantal bits verschillend: 4=n-(m+p)
Het aantal gelijk min het aantal verschillend: 1=m+p-n+m+p=2m+2p-n
Het gemeenschappelijk punt 111000000 projecteren we dan in de ruimte van M, namelijk 111001111.
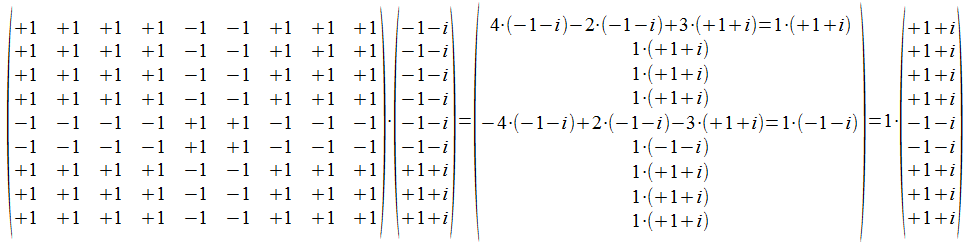
We berekenen het inwendig product van het gemeenschappelijk punt met de resultaat vector.
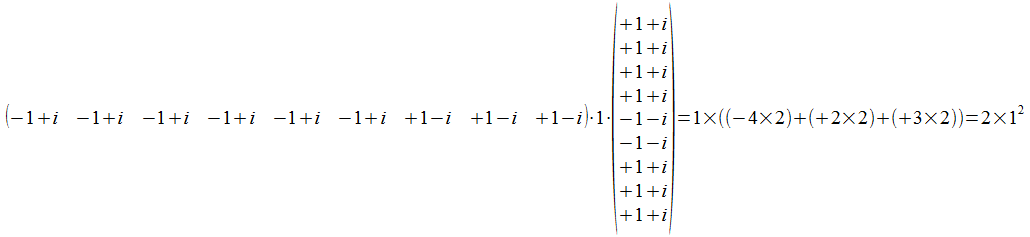
Inderdaad het gewicht van M of (m1)(p0)111... is 2(-n+2m+2p)2 en in dit concrete geval 2×12
Het gemeenschappelijk punt is xxx000000
m=3, p=2
n-m-p= 4
Het gemeenschappelijk punt xxx000000 projecteren we eerst in de ruimte van M<>, namelijk xxxxx0000.

Het inwendig product van het gemeenschappelijk punt met de resultaatvector
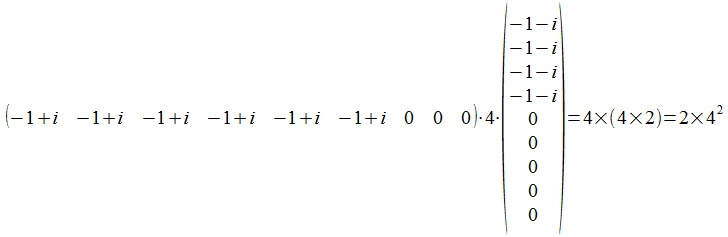
De waarnemingscontext wordt gerealiseerd door 4 atomen.
Inderdaad het gewicht van (mx)(px)000…is 2(n-m-p)2 en in dit concrete geval 2×42
Met de juiste factoren is dit 2n2w
Want
w=n-2(n-m-p)2=9-2(9-3-2)2
w<>=n-2p2
Het gemeenschappelijk punt xxx000000 projecteren we nu in de ruimte van M, namelijk xxx00xxxx.
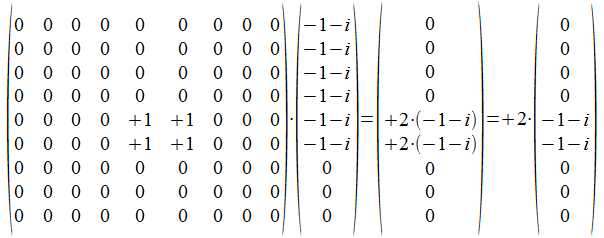
Het inwendig product van het gemeenschappelijk punt met de resultaat vector
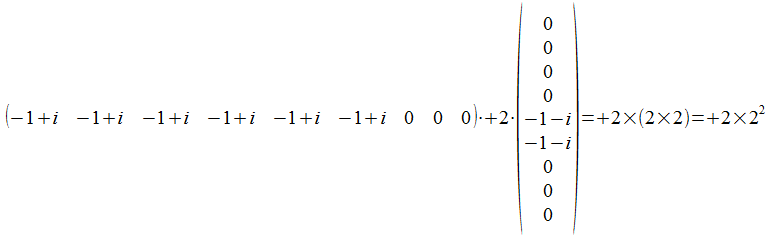
De waarnemingscontext wordt gerealiseerd door 2 atomen.
Inderdaad het gewicht van (mx)(p0)xxx… is 2p2 en in dit concrete geval 2×22
Met de juiste factoren is dit 2n2w<>
Want w<>=n-2p2=9-222
De coëfficiënt 2 is een gevolg van de normalisatie die we moeten doorvoeren om projectoren te krijgen (die dus orthogonaal zijn) en dat kunnen we nu interpreteren als het feit dat het operator formalisme geen onderscheid kan maken tussen AND-atomen en OR-atomen, ze worden eigenlijk dubbel geteld.
De coëfficiënt 2 verdwijnt natuurlijk als we de fracties van de waarnemingen berekenen:
4.21/2(4+2)-12-1/2=4/6
en
2.21/2(4+2)-12-1/2=2/6
en dus 4/6+2/6=1.