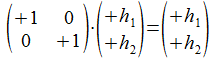
Met behulp van enkele van de meest primitieve operaties die in staat zijn te opereren op een 1-splitsing kunnen we nu samenstellingen maken. De symmetrie uit zich doordat het kwadraat van de operaties de toestand van waar men vertrokken is terug herstelt. De haakvector h die we dan voorstellen als het koppel (h₁, h₂) gedraagt zich dan als een twee dimensionale structuur. Een concrete toepassing hiervoor is de modellering van de “symmetrieën van een object in een vlak”. Het koppel (h₁, h₂) is dan beperkt tot een koppel van twee reële getallen, symbolen die verder geen structuur informatie meer dragen en de intensiteit geven van twee orthogonale eenheidsvectoren. Het object wordt dan gemodelleerd door een verzameling koppels.

Commutatieve symmetrie

De operator ε: de identiteitsoperator of 1

Kwadrateren van deze operatie levert de identiteitsmatrix.

De operator -ε: de puntspiegeling of O

Kwadrateren van deze operatie levert de identiteitsmatrix.

De operator ν: de horizontale spiegeling of H

Kwadrateren van deze operatie levert de identiteitsmatrix.

De operator -ν: de verticale spiegeling of V

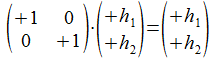
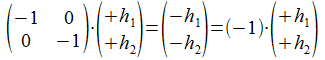
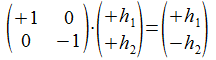
Kwadrateren van deze operatie levert de identiteitsmatrix.

De binaire samenstelling van deze operaties

De binaire samenstelling van deze operaties met behulp van het matrix product, noem dit (...S...), kunnen we voorstellen in de bekende tabel:

Dit herkennen we natuurlijk als het patroon van een Cayley tabel en de viergroep van Klein.

Ook met het creatief product hebben we structuren gevonden die hiermee isomorf zijn.

En ook:

Voorbeeld

We kunnen de 26 hoofdletters van het alfabet in hun meest typografisch symmetrische vorm in 5 soorten onderbrengen op basis van de symmetrieën uit de tabel.

{A, M, T, U, V, W, Y} hebben de 1 en V symmetrieën

{B, C, D, E} hebben de 1 en H symmetrieën

{N, S, Z} hebben de 1 en O symmetrieën

{H, I, O, X} hebben de 1, H, V en O symmetrieën

{F, G, J, K, L, P, Q, R} hebben enkel de 1 symmetrie

Niet commutatieve symmetrie

Het een onderscheiding universum is op vier manieren op een matrix voorstelling af te beelden. Dat betekent dat met vier verschillende structuren de impact van een laatst toegevoegde onderscheiding kan gemodelleerd worden.

Hieronder een voorbeeld voor de diëder groep van orde 8 (de symmetrieën van een vierkant). De laatst toegevoegde onderscheiding genereert het spoor a₀ in het geval van een rotatie en het spoor a₁ in het geval van een spiegeling.

De set (ε, νυ) als rotatie

De set (υ, ν) als spiegeling

Cayley tabel