Onderscheiding
Operator naam
Operator matrix
<<>>
1
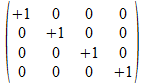
<>
-1
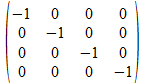
<a•b>
-j
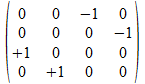
a•b
+j
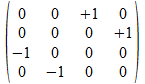
<a•c>
-k
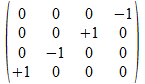
a•c
+k
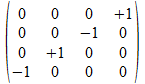
<b•c>
-i
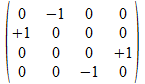
b•c
+i
Een twee onderscheidingen universum dat ingebed is in het drie-onderscheidingen universum kan verschillende isomorfe afbeelding krijgen met 4x4 matrices die operatoren zijn van het 2-splitsing universum. Er is een afbeelding mogelijk, gebaseerd op de set die voldoet aan de normale regels van Hamilton, en een gebaseerd op de reverse regels van Hamilton. We ontwikkelen nu een afbeelding gebaseerd op de set die de reverse regels van Hamilton volgt, de afbeelding gebaseerd op de andere set verloopt analoog.
We geven de volgende één-op-één vertaling:
|
Onderscheiding |
Operator naam |
Operator matrix |
|
<<>> |
1 |
|
|
<> |
-1 |
|
|
<a•b> |
-j |
|
|
a•b |
+j |
|
|
<a•c> |
-k |
|
|
a•c |
+k |
|
|
<b•c> |
-i |
|
|
b•c |
+i |
|
Hiermee bouwen we de volgende eerste tabel met overeenkomsten:
|
Matrix product van gecollapste operatoren |
Som van basis operatoren |
Drie onderscheidingen haakvector |
Drie onderscheidingen bitstring |
|
(1+j)×(1+k)=(1+k)×(1+i)=(1+i)×(1+j) |
1-(-j-k-i) |
<<>>⊕a•b⊕a•c⊕b•c |
+xxxxxx+ |
|
(1-k)×(1-i) |
1+(+j-k-i) |
<<>>⊕a•b⊕<a•c>⊕<b•c> |
xxx++xxx |
|
(1-i)×(1-j) |
1+(-j+k-i) |
<<>>⊕<a•b>⊕a•c⊕<b•c> |
xx+xx+xx |
|
(1-j)×(1-k) |
1+(-j-k+i) |
<<>>⊕<a•b>⊕<a•c>⊕b•c |
x+xxxx+x |
Merk op dat het 3+1 patroon in de som van basis operatoren op twee niveau's vast te stellen is.
Hiermee kan dan de al-nul vector in een drie-dimensionaal universum met telbare assen geïntroduceerd worden.
Merk op dat 1-j-k-i en 1-(-j-k-i) met elkaar gerelateerd zijn als een soort toegevoegde. In de literatuur over quaternionen worden beide elkaars geconjugeerde genoemd. Conjugatie is dus een involutie die een welgevormde haakuitdrukking in een gecollapste verandert en omgekeerd.
Merk op dat 1-j-k-i en 1-(-j-k-i) ook kunnen geschreven worden als 1+1-j+1-k+1-i en 1-(1-j+1-k+1-i) waarbij dus, in plaats van een som van basis operatoren, een som van gecollapste operatoren optreedt.
Nu volgt de tweede tabel met overeenkomsten:
|
Matrix product van gecollapste operatoren |
Som van basis operatoren |
Drie onderscheidingen haakvector |
Drie onderscheidingen bitstring |
|
(1+k)×(1+i)=(1-j)×(1+i)=(1+i)×(1-j) |
1-(+j-k-i) |
<<>>⊕<a•b>⊕a•c⊕b•c |
---++--- |
|
(1-k)×(1+j) |
1+(+j-k+i) |
<<>>⊕a•b⊕<a•c>⊕b•c |
--+--+-- |
|
(1+j)×(1-i) |
1+(+j+k-i) |
<<>>⊕a•b⊕a•c⊕<b•c> |
-+----+- |
|
(1-i)×(1-k) |
1+(-j-k-i) |
<<>>⊕<a•b>⊕<a•c>⊕<b•c> |
+------+ |
Merk op dat ook 1+j-k-i en 1-(+j-k-i) elkaars geconjugeerde zijn en dat ook hier het 3+1 patroon in de som van basis operatoren op twee niveau's vast te stellen is.
Een volledig analoge uitwerking kan volgen voor de set die de normale regels van Hamilton volgt.
Merk op dat voor deze afbeelding niet genoeg onderscheiding mogelijk is om alle 8 bits van de drie onderscheidingen bitstring van elkaar te onderscheiden. Dit zal pas volledig kunnen door over te gaan op een 3-splitsing universum.