We hebben gezien dat uit de meting (aan sporen van een spontaan proces) van een intensiteitsverschil in een bepaald tijdsverschil de eigenwaarde van een spontaan proces kan afgeleid worden. Een belangrijk inzicht dat hieraan voorafgaat en de verschillen een abstracte betekenis geeft, is dat dit afhankelijk is van de manier waarop toestanden elkaar uitsluiten, dus dat dit afhankelijk is van de waarnemingsresolutie van het agens-in-context, zowel wat betreft de veranderende entiteit, als wat betreft tijdsverschil, als wat betreft eigenwaarde, als wat betreft de onderverdelingen van deze parameters. De combinatie van deze drie parameters levert dan de waar te nemen intensiteit op (en dus ook de resolutie hiervan). Als we deelaspecten en hun eigenwaarde in het proces waarnemen, dan kunnen we ook hieruit een totaal proces construeren doordat we er in geslaagd zijn om de impact van een deelproces op het totale proces te modelleren door een lading toe te kennen aan een genormaliseerd deelproces. We konden normaliseren door uit te drukken dat ook stabiliteit (invariantie) in het totaal proces moet mogelijk zijn. Stabiliteit is immers de uitdrukking van het feit dat sommige aspecten niet (waarneembaar) veranderen.

We zullen nu de normalisatie verder uitbreiden voor de verschillen van intensiteiten die zich gedragen als nieuwe entiteiten en die aanleiding gaven tot producten van factoren k en (1±k). We veronderstellen daartoe dat twee nieuwe entiteiten (de constante waarde uit “de derde en de vierde kolom”) kunnen interageren in hetzelfde proces en om die interactie te modelleren moeten we terug in staat zijn te normaliseren op een zodanige manier dat een steady state kan gemodelleerd worden.

Om hiervan een voorbeeld te geven kunnen we een slinger modelleren. De slinger kunnen we waarnemen door als niet veranderende entiteit de energie te nemen en de twee nieuwe entiteiten die de steady state construeren zijn de hoeksnelheid (∼ kinetische energie) en de hoekversnelling (∼ potentiële energie).

Zoals de veronderstelling dat k=0 een constante (x-x₀) opleverde (en er dus geen verandering, geen snelheid, geen versnelling), kunnen we nu ook onderzoeken onder welke voorwaarden de verandering van intensiteit als constant verondersteld kan worden. We merken daartoe op dat de constante (x-x₀) ook bereikt wordt door normalisatie van de intensiteit bij elke stap met (1±k)ⁿ. Op die manier konden positieve en negatieve feedback op dezelfde eenheid gemodelleerd worden en dus een steady state proces: de hoeveelheid die toeneemt is exact de hoeveelheid die afneemt. Hierdoor geïnspireerd zullen we nu normaliseren met (k(1+k)ⁿ(1+k)^n-1) en dit is dan de normalisatiefactor voor twee simultaan veranderende entiteiten, namelijk de tweede kolom en de derde kolom. Dit kan dan resulteren in bijvoorbeeld een hoeveelheid die toeneemt in de tweede kolom die exact overeenkomt met een hoeveelheid die afneemt in de derde kolom. Dat zou dan gemodelleerd worden door (k(1+k)ⁿ(1-k)^n-1).

We zullen nu aantonen dat een constante eigenwaarde (maat van verandering) bereikt wordt door een normalisatie van de intensiteit bij elke stap met (k(1+k)ⁿ(1+k)^n-1)^q waarbij de waarde van q gelijk is aan 0,5, voor andere waarden van q geldt dat niet. Hierbij moeten we opmerken dat n staat voor de (tijd)stap en n-1 staat voor een kleinere stap (bijvoorbeeld de voorgaande (tijd)stap), dit zijn dus getallen afhankelijk van de resolutie van de (tijd)stap en de uitbreiding met k/h ligt dan voor de hand. Voor negatieve k zullen we dan imaginaire getallen nodig hebben (wortel van een negatief getal). Met dezelfde normalisatie factor is trouwens ook de intensiteit van de veranderende entititeit zelf (zijn snelheid) een constante.

Bewijs (met als voorbeeld de positieve feedback)

We normaliseren de intensiteit en construeren dus de functie die overeenkomt met de genormaliseerde entiteit (x-x₀)

(1+k)ⁿ/(k(1+k)ⁿ(1+k)^n-1)^0,5

We onderzoeken hiervan de natuurlijke logaritme

nln(1+k)-0,5lnk-0,5nln(1+k)-0,5(n-1)ln(1+k)

nln(1+k)-0,5lnk-0,5nln(1+k)-0,5nln(1+k)+0,5ln(1+k)

nln(1+k)-0,5lnk-nln(1+k)+0,5ln(1+k)

Bij deze stap wordt dus duidelijk dat enkel bij de lading gelijk aan 0,5 de stap afhankelijke term nln(1+k) verdwijnt.

-0,5lnk+0,5ln(1+k)

Dit is de natuurlijke logaritme van de constante (1+k)^0,5/k^0,5 of dus (1+1/k)^0,5

QED

We normaliseren nu de verandering van intensiteit en construeren dus de functie die overeenkomt met de genormaliseerde verandering van de entiteit (x-x₀)

k(1+k)^n-1/(k(1+k)ⁿ(1+k)^n-1)^0,5

We onderzoeken hiervan de natuurlijke logaritme

lnk +(n-1)ln(1+k)-0,5lnk-0,5nln(1+k)-0,5(n-1)ln(1+k)

lnk + nln(1+k)-ln(1+k)-0,5lnk-0,5nln(1+k)-0,5nln(1+k)+0,5ln(1+k)

nln(1+k)+0,5lnk-nln(1+k)-0,5ln(1+k)

Bij deze stap wordt dus duidelijk dat enkel bij de lading gelijk aan 0,5 de tijd afhankelijke term nln(1+k) verdwijnt.

+0,5lnk-0,5ln(1+k)

Dit is de natuurlijke logaritme van de constante k^0,5/(1+k)^0,5 of dus (k/(1+k))^0,5

QED

Merk op dat de vermenigvuldiging van (1+k)^0,5/k^0,5 en k^0,5/(1+k)^0,5 gelijk is aan 1.

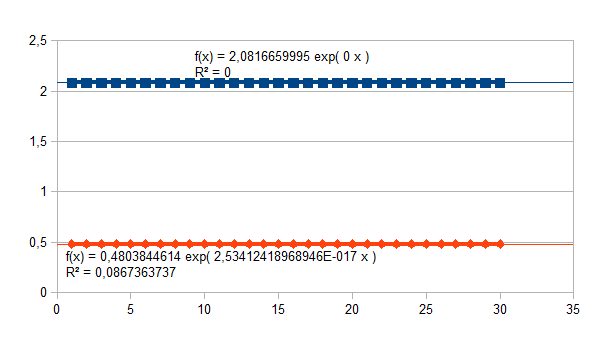
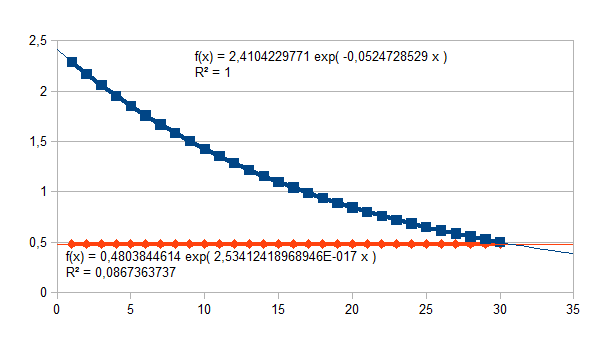
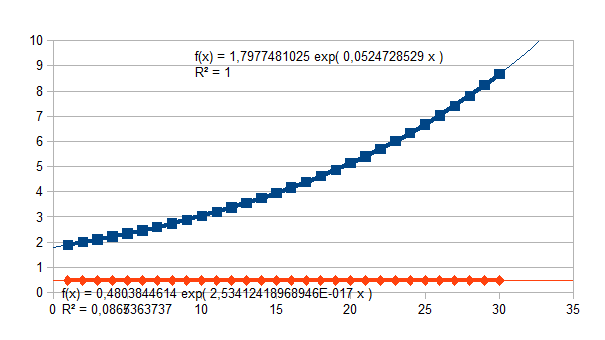
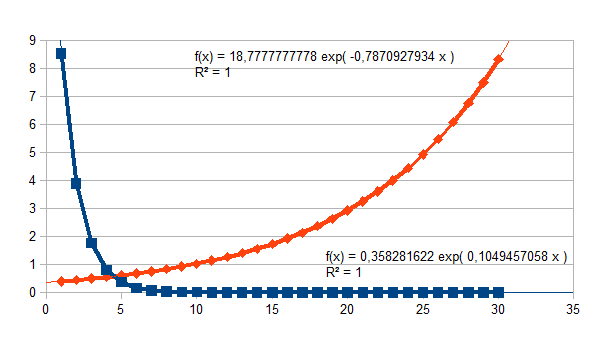
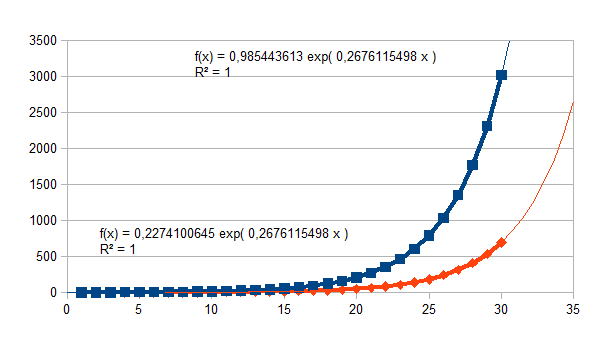
We geven nu een aantal voorbeelden van de invloed van verschillende ladingen van de intensiteit van de eenheid en de intensiteit van verandering van de eenheid. De functie (1+k)ⁿ/(k(1+k)ⁿ(1+k)^n-1)^q stellen we voor door vierkante datapunten, de functie k(1+k)^n-1/(k(1+k)ⁿ(1+k)^n-1)^p stellen we voor door ruit datapunten. De voorbeelden geven 30 stappen in de tijd. Een lading groter dan 0,5 resulteert in een negatieve feedback, een lading kleiner dan 0,5 resulteert in een positieve feedback. Het eerste voorbeeld geeft de stabiele intensiteit van de entiteit (x-x₀), namelijk 2,0816659995, en de stabiele intensiteit van de verandering van de entiteit, namelijk 0,4803844614, en dat met de beperking van de resolutie van de software en hardware. Het laatste voorbeeld geeft een keuze waarin q+p=1, en waarbij dus het product ((1+k)ⁿ/(k(1+k)ⁿ(1+k)^n-1)^q )*( k(1+k)^n-1/(k(1+k)ⁿ(1+k)^n-1)^p)=1.

De verandering van de verandering van intensiteit normaliseren

We normaliseren nu de verandering van de verandering van intensiteit en construeren eerst de normalisatiefunctie: k³(1+k)ⁿ(1+k)^n-1(1+k)^n-2, namelijk het product van (1+k)ⁿ, k(1+k)^n-1, en k²(1+k)^n-2.

Hiermee construeren we functie die overeenkomt met de genormaliseerde “snelheid van versnelling” van de entiteit (x-x₀) met lading r.

k²(1+k)^n-2/(k³(1+k)ⁿ(1+k)^n-1(1+k)^n-2)^r

We onderzoeken hiervan de natuurlijke logaritme

2lnk+(n-2)ln(1+k)-3rlnk-rnln(1+k)-r(n-1)ln(1+k)-r(n-2)ln(1+k)

2lnk+nln(1+k)-2ln(1+k)-3rlnk-rnln(1+k)-rnln(1+k)+rln(1+k)-rnln(1+k)+2rln(1+k)

2lnk-3rlnk-2ln(1+k)+3rln(1+k)+nln(1+k)-3rnln(1+k)

(2-3r)lnk+(3r-2)ln(1+k)+(1-3r)nln(1+k)

Dit maakt duidelijk dat enkel bij de lading gelijk aan 1/3 de stap afhankelijke term nln(1+k) verdwijnt.

Voor die lading reduceert de natuurlijke logaritme van de functie tot lnk-ln(1+k) of dus de functie k/(1+k)

We merken nu op dat de versnelling term dan wordt:

k(1+k)^n-1/(k³(1+k)ⁿ(1+k)^n-1(1+k)^n-2)^r

We onderzoeken hiervan de natuurlijke logaritme

lnk+(n-1)ln(1+k)-3rlnk-rnln(1+k)-r(n-1)ln(1+k)-r(n-2)ln(1+k)

lnk+nln(1+k)-ln(1+k)-3rlnk-rnln(1+k)-rnln(1+k)+rln(1+k)-rnln(1+k)+2rln(1+k)

lnk-3rlnk-ln(1+k)+3rln(1+k)+nln(1+k)-rnln(1+k)-rnln(1+k)-rnln(1+k)

(1-3r)lnk+(3r-1)ln(1+k)+(1-3r)nln(1+k)

Bij r gelijk aan 1/3 blijft geen term meer over. Dit maakt duidelijk dat de functie die de snelheid van verandering geeft dan waarde 1 heeft en dit is onafhankelijk van k. Dus de entiteit die met de stabiele snelheid van verandering overeenkomt is (x-x₀).

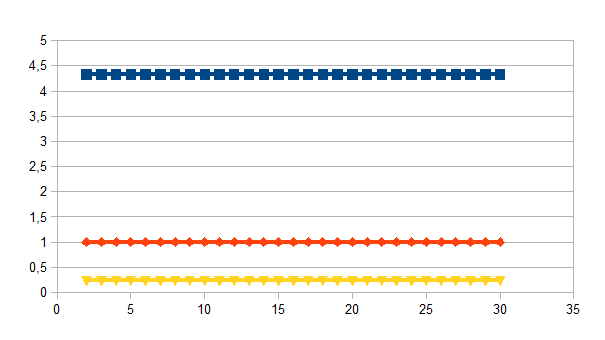
In de onderstaande grafiek zijn de drie stabiele entititeiten weergegeven in de loop van 30 stappen en dus voor r=1/3, en dat met de beperking van de resolutie van de software en hardware:

(1+k)ⁿ/(k³(1+k)ⁿ(1+k)^n-1(1+k)^n-2)^r wordt dan 4,3333333333(x-x₀) als de intensiteit van (x-x₀),

k(1+k)^n-1/(k³(1+k)ⁿ(1+k)^n-1(1+k)^n-2)^r wordt dan (x-x₀) als de intensiteit van de verandering van (x-x₀),

k²(1+k)^n-2/(k³(1+k)ⁿ(1+k)^n-1(1+k)^n-2)^r wordt dan 0,2307692308(x-x₀) als de intensiteit van de verandering van verandering van (x-x₀). Uiteraard is het product van deze drie intensiteiten (dus 4,3333333333*1* 0,2307692308) gelijk aan 1.

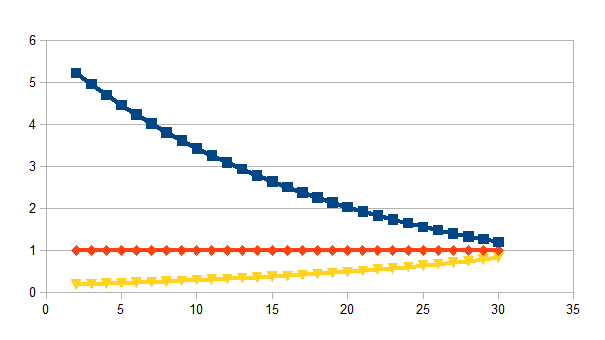
We hebben nu de lading r als de enige parameter en in principe hebben de drie termen een lading die onafhankelijk is van elkaar. We kunnen echter ook veronderstellen dat de ladingen met elkaar gekoppeld zijn en dus ladingen zijn van dezelfde entiteit. Inderdaad kunnen we nu de versnelling als constant beschouwen en zorgen dat het product van beide andere intensiteiten gelijk is aan 1 voor elke tijdstap. We geven hiervan een voorbeeld met k=0,3, r₁=0,4, r₂=1/3 en r₃=1-0,4-1/3:

Bij een k=0,5 wordt dan het volgende verband gevonden:

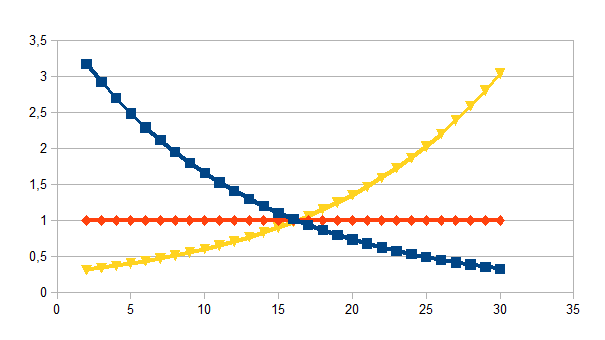
Door de eigenwaarde k in deelintervallen op te splitsen kan voor een waarde van n/0,9922737798 het punt gevonden worden waarbij de intensiteit van de drie processen niet verschillend zijn van elkaar en dus gelijk zijn aan 1.

We veronderstellen nu dat de ladingen r₁ en r₃ ook afhankelijk zijn van de tijdstap n. De som van drie ladingen moet 1 zijn, dus sin² + cos²=2/3 geeft de relatie tussen de intensiteit op elk moment en de verandering van de verandering van intensiteit bij een constante verandering van intensiteit. De tijdstap wordt dan de hoek α, de lading wordt dus afhankelijk van α. sin²=tg²/1+tg² en cos²=1/1+tg². Hierbij wordt die hoek geconstrueerd die inderdaad waarneembaar is aan een slinger in een veld met constante versnelling (het zwaartekracht veld).