De genetische codes kunnen bestudeerd worden vanuit het abstracte standpunt van informatie overdracht bij het proces van synthese van eiwitten. De codes zijn immers in staat structuur informatie over te dragen in een omgeving met zeer veel ruis, storingen, mutaties enz.… Sinds we beschikken over computers en software en zelf informatie willen communiceren (en daarom moeten coderen) weten we dat in principe een binaire codering kan gebruikt worden om gelijk welke willekeurig optredende fout in het communicatiekanaal te corrigeren. De inzichten die hierbij ontstaan zijn inspireren verschillende onderzoekers van de genetische code. Daartoe onderscheiden ze verschillende discrete repertoria (dit noemen ze verschillende alfabetten) van moleculaire bouwstenen zoals het 4-letter alfabet van nucleotiden, het 64-letter alfabet van triplets van die basen, het 20-letter alfabet van de aminozuren die met deze nucleotiden gesynthetiseerd worden, het 2-letter alfabet van de sterke en zwakke duplets, en hogere alfabetten van multiplets. Elke sequentie van nucleotiden kan gelezen worden vanuit een ander repertorium dat daarmee een ander standpunt mogelijk maakt. Die kracht herkennen we ook in het haakformalisme: een symbool heeft geen éénduidige betekenis, een welgevormde haakuitdrukking in twee symbolen kan indien nodig gelezen worden als haakuitdrukking in meerdere symbolen. Het moet dus mogelijk zijn om deze onderzoeken in het haakformalisme te modelleren. We laten ons dus inspireren door deze onderzoeken, maar geven de onderzoeken een diepere en fundamentelere basis: het enige dat we nodig hebben is het binaire onderscheid tussen “iets” en “iets anders”.

Dit blijkt verrassend eenvoudig te zijn wanneer we vertrekken van de vier nucleotiden: C, A, G en U/T die de nucleïnezuren RNA en DNA opbouwen, maar ook een belangrijke rol spelen bij het energietransport in de cel enz.... U komt voor in het RNA, T komt voor in het DNA. Het verschil tussen U en T is een -CH₃ groep. We herkennen de 3&1 opdeling waarin U/T zich ten opzichte van de drie andere positioneert. De nucleotide U (en ook zo voor T) is de enige zonder een -NH₂ groep.

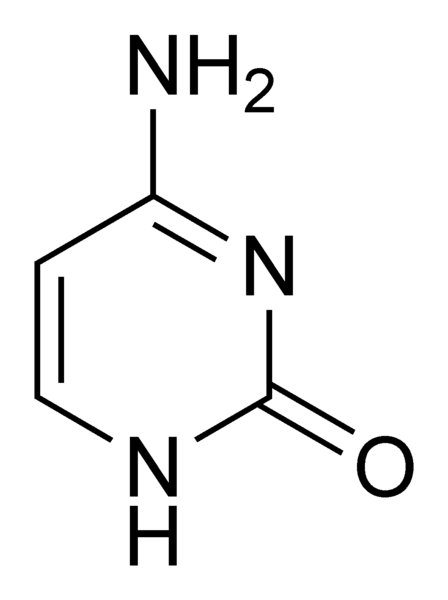
In de volgende tabel geven we de namen en een van de isomeren van de nucleotiden en een deel van de duale classificatie die we nog verder zullen gebruiken om de structuur in het haakformalisme te vertalen. Het eerste onderscheid is een tussen een molecule met enkelvoudige ring (in dit geval een pyrimidine) en een molecule met een dubbele ring (in dit geval een purine). Het tweede onderscheid is een classificatie op basis van de reactiviteit van de amino-groep met HNO₂ (reactief, gecodeerd als amino versus niet reactief, gecodeerd als keto). Beide spelen een rol in de mogelijke mutaties van α-amino-zuren (zuren met zowel een -NH₂ goep als een -COOH groep op hetzelfde koolstofatoom).

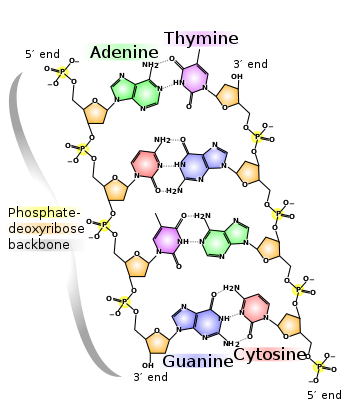
De vier gematerialiseerde structuren zijn sporen van reacties die stabiel zijn in het milieu van de cel en als sporen kunnen ze met elkaar gecombineerd worden waarbij nieuwe sporen ontstaan enz.... Hoe die allemaal kunnen gecombineerd worden in de opbouw van DNA met zijn fosfaat-desoxyribose (suiker) ruggengraat en dubbele helix is voorgesteld in het volgende voorbeeld waarin we links de sequentie ACGT van boven naar onder lezen en rechts dezelfde sequentie van onder naar boven:

Het DNA is immers opgebouwd met complementaire strings en de complementariteit is het gevolg van waterstofbruggen tussen specifieke baseparen, elektrostatische bindingen tussen molecules die (gemakkelijker dan de andere bindingen) gemaakt of verbroken worden. Om de richting van de strings te coderen gebruikt men de standaard nummering van de ring in de deoxyribose ruggengraat die de fosfaatgroepen met elkaar verbindt.

Waterstofbruggen zijn enkel te onderscheiden bij duplets. Waterstofbruggen zijn op het eerste zicht geen binaire onderscheiding, aangezien een molecule die 3 waterstofbruggen kan aangaan ook 2 waterstofbruggen kan aangaan, maar omgekeerd is dat niet mogelijk. Nochtans wordt dat in de natuur niet waargenomen doordat er ook een ruimtelijke overeenkomst moet zijn tussen de functionele groepen die waterstof kunnen aanbieden en ontvangen. Uitzonderingen hierop is het “wobble pair” GU met 2 H-bruggen in plaats van 3 H-bruggen.

Hierbij de zes mogelijkheden van duplets van nucleotiden, maar enkel de varianten met een x worden waargenomen:

Dus enkel de waterstofbruggen tussen CG (namelijk 3) en AU (namelijk 2) hebben een stabiele structurele functie. Maar er zijn nog meer ruimtelijke mogelijkheden en onmogelijkheden die dan kunnen leiden tot nieuwe binaire onderscheiden die een rol kunnen spelen in de informatieoverdracht van chemische reacties met nucleotiden (een ervan hebben we al gezien als “wobble pair”). Het zijn dus de duplets die de driedimensionale ruimte binnenbrengen in de modellering. Een voorbeeld van de ruimtelijk bepaalde waterstofbruggen (3 in het linker deel, 2 in het rechterdeel) dank zij de overeenkomende lengte van de componenten is gegeven in de schematische voorstelling van een deel van de dubbele string van RNA.

De vier nucleotiden kunnen we dus beschouwen als gebaseerd op drie binaire onderscheidingen: pyrimidine versus purine, amino versus keto, en 3 versus 2 mogelijkheden tot waterstofbruggen. Dit brengt ons tot het volgende overzicht:

De vertaling naar onderscheidingen

De binaire onderscheiding pyrimidine versus purine noemen we nu a versus <a>, keto versus amino noemen we b versus <b>, 2 versus 3 waterstofbruggen noemen we c ten opzichte van <c>. Dus bijvoorbeeld: cytosine is gemodelleerd als de conjunctie van pyrimidine, amino, 3H-bruggen of dus als welgevormde haakuitdrukking: <<a><<b>><<c>>>. Dit is zinvol omdat we de nucleotiden inderdaad als sporen kunnen afscheiden en ze elkaar dan uitsluiten, onze meetcontext is zodanig dat we daarin slagen en dat we er kunnen van uitgaan dat dit betekenis geeft aan een concatenatie van sporen: een mogelijke genetische code bijvoorbeeld: ...CUAAGAGUAGG… Die concatenatie wordt dan uitgelezen door een transfermolecule juist doordat er met behulp van lokaal stabiele waterstofbruggen twee reactiekernen in contact met elkaar gebracht worden.

Met de drie binaire onderscheidingen zijn er dus acht mogelijke toestanden die een reactie kunnen uitlokken in de gepaste context. Blijkbaar zijn er maar vier gematerialiseerd en als stabiele sporen beschikbaar binnen het milieu van de cel. We geven een vertaling met enkel Uracil (we concentreren ons dus nu enkel op de modellering in mRNA omdat een DNA streng één-op-één afgebeeld wordt om mRNA) die daaraan voldoet en we voegen een aantal kolommen toe aan de tabel die relaties verduidelijken.

Hiermee wordt onmiddellijk duidelijk hoe in het haakformalisme kan gemodelleerd worden dat maar die vier sporen waargenomen worden: één van de onderscheidingen is een laatst toegevoegde die dezelfde waarde heeft als het vectorproduct van de twee andere. De welgevormde haakuitdrukking is dus de contractie naar die onderscheiding onder die voorwaarde. Inderdaad: stel bijvoorbeeld c=b•a (of dus ook a=b•c of b=c•a of c•b•a=<<>> ) en in de laatste kolommen hebben we deze gelijkheid en de inbedding gerealiseerd. Dit maakt dan ook duidelijk dat de realisatie slechts drie sporen als resultaat heeft in het haakformalisme, want <Uracil> blijkt in die meetcontext niet anders te zijn dan Adenine (“het ervaren van Uracil is niet anders dan laten gebeuren van Adenine”). Het vectorproduct is een universele maar lokale relatie in het haakformalisme, A•C•G•U=<> betekent dat een 4-vector een van de twee mogelijke waarden heeft, maar betekent ook A•C•G=<U> dus de gelijkheid wat betreft waarde van een 3-vector en een 1-vector, of C•G=A•<U>, twee 2-vectoren onderscheiden zich niet.

De nucleotide U blijkt een bijzondere bouwsteen te zijn en dat is de reden waarom we ervoor kiezen om voor U dezelfde waarde te nemen voor de drie onderscheidingen. Het is de enige zonder een -NH₂ groep en we merken dat Uracil inderdaad door andere kan vervangen worden om waterstofbruggen te bouwen (bijvoorbeeld door Thymine in het DNA of Inosine in het tRNA).

Het potentieel universum wordt in die meetcontext slechts door twee onderscheidingen opgespannen en slechts drie toestanden worden gerealiseerd zoals in de onderstaande tabel duidelijk wordt. Merk op dat de vier toestanden elkaar uitsluiten, zowel in drie onderscheidingen als in twee onderscheidingen en dat ze samen een tralie opspannen die in het ervaren isomorf is met de tralie van de laatst toegevoegde onderscheiding.

Dit betekent niet meer en niet minder dat deze vier nucleotiden een universele uitdrukkingskracht hebben, immers: elke welgevormde haakuitdrukking kan in twee onderscheidingen uitgedrukt worden en het gedrag van de nucleotiden wordt door een derde onderscheiding gemodelleerd. Die derde onderscheiding is een gevolg van de interactie (en is dus een eigenschap van een duplet, de reactiekern). Dit maakt onmiddellijk ook de 3&1 structuur duidelijk. Een uitdrukking zoals bijvoorbeeld C⊕A⊕G⊕<U> is een welgevormde haakuitdrukking die niet kan onderscheiden worden van het ervaren van deze relatie. De vier nucleotiden sluiten elkaar vier-aan-vier uit (het zijn sporen) en dit is duidelijk in de tabel. De som C⊕A⊕G⊕<U> is in bitstring 1011.1111⊕1111.0111⊕1101.1111⊕0111.1111∼0001.0111. Zo zijn er 16 welgevormde haakuitdrukkingen wanneer we elk van deze vier symbolen beschouwen als een 2-vector, iets wat we altijd kunnen doen. Die 2-vectoren zijn dan in hun meest eenvoudige vorm zes mogelijke “duplets” die we hieronder gaan onderzoeken op een abstracter niveau. Inderdaad: als we bijvoorbeeld een symbool gebruiken als UACCUGAU is de concatenatie van de symbolen nog niet gemodelleerd. Het enige wat we nu kunnen is individuele symbolen als sporen in een meetproces realiseren.

Bij realisatie kunnen we drie nucleotiden dus afbeelden op drie van de vier toestanden in twee onderscheidingen en een van de nucleotiden op het ervaren supremum. We kunnen kiezen hoe we de onderscheidingen een naam geven. Een van de onderscheidingen is gebaseerd op waterstofbruggen en dit is een relatie tussen twee nucleotiden. Zij vormen samen een duplet. Wanneer we een keten van nucleotiden beschouwen dan moeten we dit minimaal altijd lezen als een keten van duplets want twee nucleotiden in dezelfde keten zouden kunnen reageren met elkaar. Twee identieke nucleotiden vormen ook een duplet en de volgorde (concatenatie) kan een rol spelen in mogelijke interpretaties van de string (CA bijvoorbeeld kan onderscheiden worden van AC, een niet-commutativiteit die we herkennen in het creatief product). Er zijn dus 4² mogelijke duplets. De 16 duplets kunnen dus 16 welgevormde haakuitdrukkingen modelleren. Verder zullen we vaststellen hoe essentieel dit is.

In wat volgt moeten we nu een selectie maken van interpretatie van de nucleotiden in de taal van het haakformalisme en we hanteren de volgende symbolen met hun voorstelling in drie onderscheidingen:

Vier 1-vectoren

1111.0111∼A

1011.1111∼C

1101.1111∼G

0111.1111∼<U>

Zes 2-vectoren

We construeren alle 2-vectoren en hun combinaties met het vectorproduct • en dat zowel als haakuitdrukking als in binaire vorm. We noemen voor het gemak een 2-vector een duplet. Noteer dat bijvoorbeeld A•<U> niet kan onderscheiden worden van <A•U> en niet kan onderscheiden worden van <U•A> en dat alle “duplets” commutatief zijn (een niet commutatieve duplet zou moeten gemodelleerd worden als een creatief product):

We nemen nu enkel de 2-vectoren uit een van de kolommen of uit een van de rijen, bijvoorbeeld

1101.0111∼A•G

0111.0111∼A•<U>

1001.1111∼C•G

0011.1111∼C•<U>

Deze vormen (als som in het 3&1 formaat) de welgevormde haakuitdrukking A•G⊕A•<U>⊕C•G⊕C•U∼0010.1000 of dus <A•G>. Dat is niet anders dan het creatief product (<A•G>⊗A•U)_A•C∼<A•C<<A•G>>><<A•C><A•U>>∼<A•C<<A•G>>>•<<A•C><A•U>>. Deze vormen van haakvectoren in 3&1 formaat zijn niet anders dan uitdrukkingen van disjunctie of conjunctie. Terwijl ook duidelijk is dat elke 2-vector de disjunctie is van twee nucleotiden (1101.0111∼A•G is de disjunctie van 1101.1111 (G) en 1111.0111 (A)) omdat de nucleotiden elkaar twee-aan-twee uitsluiten. Die disjunctie is natuurlijk ook als creatief product (dus in 3&1 formaat) op verschillende manieren uit te drukken, bijvoorbeeld (<>⊗<A>)_G∼<<>>⊕A⊕G⊕<A•G>∼(<>⊗<G>)_A∼(<>⊗<A•G>)_<A>.

De selectie van 2-vectoren uit een rij (of kolom) levert slechts vier 2-vectoren op. In het voorbeeld ontbreken A•C en <G•U> in de selectie, en dat zijn inderdaad de 2-vectoren die we kunnen beschouwen als toegevoegde voor dezelfde welgevormde haakuitdrukking. We hebben (<A•G>⊗A•U)_A•C al uitgedrukt. Er geldt bijvoorbeeld ook: (<A•G>⊗<C•G>)_<G•U>∼<<G•U><<A•G>>><<<G•U>><<C•G>>>∼A•G⊕C•G⊕A•<U>⊕C•U∼0010.1000 of dus <A•G>.

Op basis van dezelfde vier 2-vectoren kunnen nog drie ander sommen gemaakt worden die welgevormde haakuitdrukkingen zijn:

A•G⊕<A•U>⊕<C•G>⊕<C•U>∼1000.1000∼A•U

A•G⊕A•U⊕C•G⊕<C•U>∼0110.0000∼<C•G>

<A•G>⊕<A•U>⊕C•G⊕<C•U>∼1100.0000∼C•U

Elke kolom (rij) heeft een symmetrische kolom (rij) want de diagonalen geven ofwel <<>>, ofwel <A•C•G•U>, dus de vormen als sommen in 3&1 formaat geven hetzelfde resultaat in die symmetrische kolom.

Hiermee is duidelijk dat elke kolom (rij) door middel van een 3&1 som van 2-vectoren elke 2-vector kan representeren. De representatie is een creatief product en daar zijn dus drie 2-vectoren bij betrokken. Drie 2-vectoren kunnen als een triplet beschouwd worden. Een triplet blijkt een fundamentele bouwsteen te zijn in de genetische code. Een creatief product is niet commutatief en het is inderdaad bekend dat triplets in mRNA niet commutatief zijn.

We geven nu een keuze van mogelijke triplets waarvan twee 2-vectoren telkens gemeenschappelijk zijn:

(<A•G>⊗A•U)_A•C=A•G⊕<A•U>⊕C•G⊕C•U∼0010.1000∼<A•G>

(<A•G>⊗A•U)_C•G=A•G⊕<A•U>⊕A•C⊕A•C•G•U∼0000.1000∼<A>

(<A•G>⊗A•U)_<C•U>=A•G⊕<A•U>⊕<A•C•G•U>⊕<A•C>∼1010.1000∼A•G•U

(<A•G>⊗A•U)_A•G=A•G⊕<A•U>⊕<<>>⊕G•U∼0000.1000∼<A>

(<A•G>⊗A•U)_<A•U>=A•G⊕<A•U>⊕<G•U>⊕<>∼1010.1000∼A•G•U

(<A•G>⊗A•U)_<G•U>=A•G⊕<A•U>⊕<A•U>⊕<A•G>∼A•U

We zien dat er maar vier verschillende resultaten zijn, en dat er zowel 1-vectoren, 2-vectoren als 3-vectoren gegenereerd worden. De triplets die niet gelijk zijn aan een 2-vector worden in dubbel gegenereerd.

Het aantal mogelijkheden om een geordende keuze te maken van 3 verschillende elementen uit een totaal van 6 elementen, wordt gegeven door 6!/(6-3)! en dit zijn 120 mogelijkheden waarvan er dus veel dubbels zullen zijn.

Vier 3-vectoren

Met de vier 1-vectoren A, C, G en <U> kunnen we vier 3-vectoren construeren:

1001.0111∼A•C•G

0011.0111∼A•C•<U>

0101.0111∼A•G•<U>

0001.1111∼C•G•<U>

We merken nu op dat de som in het 3&1 formaat staat en dat:

A•C•G⊕A•C•<U>⊕A•G•<U>⊕C•G•<U>∼1111.1111∼<<>>

De conjunctie van de vier 3-vectoren is ook niet anders dan <<>>, dus ze sluiten elkaar (enkel als viertal) uit.

De 4-vector

Met de keuze die we maakten voor de vectoren kunnen we nu ook de 4-vector berekenen.

A•C•G•<U>∼0001.0111∼<c•b•a>⊕a⊕b⊕c

Deze welgevormde haakuitdrukking is een zelfduaal op centraal niveau in drie onderscheidingen en dit is een zeer belangrijke vaststelling. Zo zijn er 16 zelfduale welgevormde haakuitdrukkingen in drie onderscheidingen mogelijk:

Maar van die 16 mogelijkheden zijn er maar 10 die een relatie tussen drie onderscheidingen modelleren. Ze zijn twee-aan-twee elkaars inbedding. Dus als patroon zijn er maar 5 mogelijkheden. Dus er zijn 5 mogelijkheden voor de interpretatie van de 4-vector. A•C•G•<U>∼0001.0111∼<c•b•a>⊕a⊕b⊕c is maar één mogelijkheid, een andere is <c•b•a>, een andere c•b•a⊕a⊕<b>⊕c enz…, telkens overeenkomend met een andere keuze van hoe de onderscheidingen als symbolen gebruikt worden.

Elke interpretatie genereert dan vier 3-vectoren (die van die 4-vector afgeleid worden) en dus in het totaal zijn er 20 3-vectoren te onderscheiden en verschillende zullen overlappen (en dus niet uniek zijn). Dit illustreert wel de robuustheid van de genetische code en de gelijkwaardigheid van verschillende triplets, maar om het verband te zien met het bestaan van 20 essentiële aminozuren (die dus wel uniek zijn) moeten we de structuur nog een stuk verder ontwikkelen.

De vijf tralies van de 4-vectoren

Met de vier vectoren A, C, G en <U> kunnen we vier 3-vectoren construeren:

A•C•G∼ACG∼1001.0111∼<<c•b•a><<b><a>>>∼<<>>⊕<a>⊕<b>⊕<c>⊕b•a⊕c•a⊕c•b

A•C•<U>∼AC<U>∼0011.0111∼<b<<c><a>>>∼<<>>⊕<a>⊕<c>⊕<b•a>c•a⊕<c•b>⊕c•b•a

A•G•<U>∼AG<U>∼0101.0111∼<a<<c><b>>>∼<<>>⊕<b>⊕<c>⊕<b•a>⊕<c•a>⊕c•b⊕c•b•a

C•G•<U>∼CG<U>∼0001.1111∼<c<<b><a>>>∼<<>>⊕<a>⊕<b>⊕b•a⊕<c•a>⊕<c•b>⊕c•b•a

Dit bevestigt ook dat de som in het 3&1 formaat staat en dat: A•C•G⊕A•C•<U>⊕A•G•<U>⊕C•G•<U>∼1111.1111∼<<>>

De zes 2-vectoren zijn dan:

A•C∼AC∼1011.0111∼<b<c•a>>∼<>⊕b⊕<c•a>⊕<c•b•a>

A•G∼AG∼1101.0111∼<a<c•b>>∼<>⊕a⊕<c•b>⊕<c•b•a>

A•<U>∼A<U>∼0111.0111∼<ba>∼<>⊕a⊕b⊕b•a

C•G∼CG∼1001.1111∼<c<b•a>>∼<>⊕c⊕<b•a>⊕<c•b•a>

C•<U>∼C<U>∼0011.1111∼<cb>∼<>⊕c⊕b⊕b•c

G•<U>∼G<U>∼0101.1111∼<ca>∼<>⊕a⊕c⊕c•a

Dit maakt duidelijk dat bijvoorbeeld geldt dat

A<<A•C>>∼<<A•C>> maar A•<<A•C>>∼C

A•C•G∼ACG∼1001.0111∼<<A•C>><<A•G>>

Het resultaat is als een volledige tralie af te beelden. We herkennen de tralie als de structuur van de tralie van het twee onderscheidingen universum. Het belangrijk verschil is dat geen enkel punt van de tralie de inbedding is van een ander punt. Elk punt van de tralie is als creatief product te schrijven en dat creatief product heeft dus drie componenten.

Zo zijn er dus vijf mogelijke tralies tussen de vijf 4-vectoren en de gemeenschappelijke <<>>, en de inbedding van die vijf mogelijke tralies tussen de 4-vectoren en <>.

Overzicht

We construeren nu expliciet de vijf mogelijkheden. We hebben gekozen om <U> gemeenschappelijk te nemen voor de vijf mogelijkheden. De ingebedde waarde van U genereert dan de andere vijf mogelijkheden. Aan de index van de symbolen kan men de tralie afleiden. Het symbool U geven we dus geen index. Een gevolg hiervan is dat er maar 7 atomen van de 8 mogelijke atomen van het drie onderscheidingen universum in de 5 tralies voorkomen. We komen daar verder op terug.

De tralies zijn ook gemakkelijk te lezen door enkel de bitstrings te gebruiken. Enkel voor de atomen van de tralies vermelden we in het overzicht hieronder ook de haakuitdrukking en de haakvector. In drie onderscheidingen zijn er maar 8 atomen en dus zullen de tralies overlappen. We geven in de onderstaande tabellen de gelijkheid van verschillende symbolen aan (gelijkheid die we dank zij de unieke bitstring kunnen herkennen).

De 2-vectoren en de 3-vectoren geven we enkel weer als haakuitdrukking in A, C, G, U en als bitstring. Het vectorproduct kan als inbedding geschreven worden, de disjunctie niet, vandaar dat we beide noteren.

De zes 2-vectoren:

De vier 3-vectoren:

De zes 2-vectoren:

De vier 3-vectoren:

De zes 2-vectoren:

De vier 3-vectoren:

De zes 2-vectoren:

De vier 3-vectoren:

De zes 2-vectoren:

De vier 3-vectoren:

Het uniek laatste atoom

Aan de index van de symbolen kan men de tralie afleiden en sommige atomen komen in twee tralies voor. Het atoom U hebben we niet voorgesteld met een index om zijn speciale positie aan te geven. Een gevolg hiervan is dat er maar 7 atomen van de 8 mogelijke atomen in de 5 tralies voorkomen.

De onderstaande tabel geeft de mogelijkheid om de 7 een unieke code te geven (tussen A en G, symbolen niet gerelateerd met de reeds gebruikte symbolen voor nucleotiden).

Van de 2-vectoren zijn dat er dan maar 18 van de 28 mogelijke zoals we in de tabel hieronder weergeven, de laatste tabel geeft de mogelijkheid om de 18 een unieke code te geven, niet gerelateerd aan de codes van de vorige tabel:

Dit wordt ook gereflecteerd in het aantal 3-vectoren die we in de tabel hieronder weergeven. Er zijn maar zeventien 3-vectoren die zich onderscheiden van in totaal 56, omdat er vier van hen dubbels zijn en alle 3-vectoren hebben één bit die dezelfde waarde heeft. De inbedding van deze zeventien modelleert de 3-vectoren met de inbedding van Uracil. De laatste tabel geeft de mogelijkheid om de 17 een unieke code te geven, niet gerelateerd aan de codes van de vorige tabel.

Elk van deze zeventien 3-vector atomen op niveau 1 van de tralies wordt gerealiseerd door drie 1-vector atomen, welke dat zijn is duidelijk in de naamgeving van de 3-vectoren.

Het unieke gemeenschappelijke atoom kan in deze tralies niet van waarde veranderen. Het wordt ook niet gemodelleerd wanneer we de vijf tralies berekenen die gebaseerd zijn op de inbedding van U. Dus dit atoom kan enkel in een groter universum gemodelleerd worden en daarom moeten we een onderscheiding bijvoegen bij de reeds gebruikte a, b en c en dus worden de bitstrings nog eens verdubbeld.

Vier onderscheidingen universum

Om alle mogelijke toestanden te modelleren die sporen kunnen zijn van processen moeten we dus overgaan naar een universum met 16 atomen en dus vier onderscheidingen. Het patroon wordt behouden zodanig dat we nu al weten dat er maar 15 atomen als tralie gemodelleerd zullen kunnen worden, maar alle atomen in drie onderscheidingen zullen wel kunnen gemodelleerd worden in vier onderscheidingen. Dit is niet anders dan het patroon dat we gebruikten toen we met dit onderzoek gestart zijn (maar dan in drie onderscheidingen): het vectorproduct van alle gebruikte onderscheidingen heeft een waarde en dat zorgt voor een contractie naar een universum met één onderscheiding minder. Dit is de universele manier waarop we in het ervaren een onderscheidingen universum kunnen contraheren naar een universum met minder onderscheidingen (en dus ook kunnen expanderen naar een met meer onderscheidingen). Dat is trouwens ook de manier waarop we afgeleiden hebben gemodelleerd in het haakformalisme en hiermee hebben we conjunctie en disjunctie kunnen uitdrukken.

Ook het patroon van dualiteit wordt gewoon verder gezet. Zoals voor drie onderscheidingen zullen ook in vier onderscheidingen zelfdualen zich enkel op centraal niveau kunnen bevinden. Andersdualen bevinden zich daar ook en het hoogste vectorproduct is nu de andersduaal d•c•b•a. Het patroon van de andere zelfdualen in drie onderscheidingen, namelijk de vier zelfdualen c•b•a⊕<a>⊕<b>⊕<c>; c•b•a⊕<a>⊕b⊕c; c•b•a⊕a⊕<b>⊕c; c•b•a⊕a⊕b⊕<c>, wordt nu uitgebreid door het vectorproduct met d, maar zowel d, c, b en a kunnen als “laatst toegevoegde” beschouwd worden. Dus de volgende uitdrukkingen zijn welgevormd: d•(c•b•a⊕<a>⊕<b>⊕<c>) maar ook c•(d•b•a⊕<a>⊕<b>⊕<d>) enz… er zijn dus veel meer relevante 4-vectoren.

Naast de andersduaal d•c•b•a genereert dit ook de volgende 16 andersdualen op centraal niveau:

11101000.00010111∼d•c•b•a⊕<d•a>⊕<d•b>⊕<d•c>

00101011.11010100∼d•c•b•a⊕<d•a>⊕d•b⊕d•c

01001101.10110010∼d•c•b•a⊕d•a⊕<d•b>⊕d•c

01110001.10001110∼d•c•b•a⊕d•a⊕d•b⊕<d•c>

11100001.10000111∼d•c•b•a⊕<c•a>⊕<c•b>⊕<d•c>

00101101.10110100∼d•c•b•a⊕<c•a>⊕c•b⊕d•c

01001011.11010010∼d•c•b•a⊕c•a⊕<c•b>⊕d•c

01111000.00011110∼d•c•b•a⊕c•a⊕c•b⊕<d•c>

11001001.10010011∼d•c•b•a⊕<b•a>⊕<c•b>⊕<d•b>

00111001.10011100∼d•c•b•a⊕<b•a>⊕c•b⊕d•b

01100011.11000110∼d•c•b•a⊕b•a⊕<c•b>⊕d•b

01101100.00110110∼d•c•b•a⊕b•a⊕c•b⊕<d•b>

10101001.10010101∼d•c•b•a⊕<b•a>⊕<c•a>⊕<d•a>

01011001.10100110∼d•c•b•a⊕<b•a>⊕c•a⊕d•a

01100101.10100110∼d•c•b•a⊕b•a⊕<c•a>⊕d•a

01101010.01010110∼d•c•b•a⊕b•a⊕c•a⊕<d•a>

Uiteraard vinden we ook hun inbeddingen terug.

We kunnen dus 16+1=17 infima onderscheiden van tralies met als supremum <<>>. Elk van deze tralies is af te beelden op de tralie van een drie onderscheidingen universum.

De uitbreiding naar nog hogere universa ligt dan voor de hand en we zullen merken dat hetzelfde spoor door meerdere atomen kan voorgesteld worden. We kunnen dan onmiddellijk afleiden dat de 3-vectoren die als dubbel voorkwamen in drie onderscheidingen, in het vier onderscheidingen universum als viervoud zullen voorkomen en de 3-vectoren die maar éénmaal voorkomen in drie onderscheidingen, als dubbel zullen voorkomen. Er zullen ook vectoren uniek zijn voor het vier onderscheidingen universum.

In de genetische code is inderdaad bekend dat meerdere triplets kunnen coderen voor hetzelfde aminozuur, het is opvallend dat de 20 essentiële aminozuren ofwel door 4, 2 of 1 triplet gecodeerd worden. Dit wijst er op dat er inderdaad vier onderscheidingen nodig zijn (en dus bitstrings van 16 bits) om dan sommige atomen vier maal terug te vinden.

Wanneer we de 20 essentiële aminozuren zouden willen coderen als unieke sporen die elkaar uitsluiten, dan is zelfs het vier onderscheidingen universum niet voldoende, en we moeten overgaan naar 5 onderscheidingen en dus 32 bits. We kunnen dit ook als volgt benaderen: de dynamiek van vier nucleotiden vereist de modellering in drie onderscheidingen en de laatst toegevoegde onderscheiding modelleert wat het spoor zal zijn bij de volgende stap. Dit vereist in binair formaat 8 bits. Elk van deze bits kunnen we vervangen door vier bits van het twee-onderscheidingen universum (de som van de vier nucleotiden in een mogelijk 3&1 formaat). In totaal hebben we dan 32 bits nodig.

Als we dit willen realiseren als sporen die achtergelaten kunnen worden dan kunnen we niet anders dan overgaan naar triplets. Er zijn 4³ mogelijkheden hiervoor, dus 64 en twee maal te veel. Het blijkt nu dat de 20 aminozuren die essentiëel zijn voor het leven gecodeerd worden door de 64 mogelijke triplets van nucleotiden, dat meerdere triplets hetzelfde aminozuur genereren en dat sommige triplets als start en stop van een proces functioneren. Deze redundantie zorgt ervoor dat niet alle mutaties van nucleotiden gevolgen zullen hebben, wat goed is voor de robuustheid van het systeem voor de gevolgen van willekeurige mutaties.

Zoals we dus relaties gevonden hebben tussen de 4 nucleotiden, zullen we ook relaties vinden tussen de triplets als we bestuderen hoe ze gerelateerd zijn met de 20 aminozuren. Dit wordt onmiddellijk veel complexer omdat het tRNA ook met andere nucleotiden dan deze in het mRNA koppels kan vormen (het zogenaamde “wobble pairing”), maar we verwachten dat het patroon zich zal herhalen bij het toevoegen van nieuwe onderscheidingen bovenop de purine/pyrimidine, keto/amino en 2H/3H onderscheidingen.

Triplets en individuele nucleotiden worden in het haakformalisme gemodelleerd door een creatief product en dat is een universele voorstelling van een welgevormde haakuitdrukking. Een mRNA sequentie is dan een conjunctie (of disjunctie) die lokaal uitgelezen wordt door de eenvoudige vergelijking van duplets: een nucleotide van het mRNA en een van het tRNA.