De matrix voorstelling van het 1 splitsing universum maakt het mogelijk om verschillende uitbreidingen te onderscheiden en te bestuderen. We geven hiervan een aantal voorbeelden, waarbij het patroon duidelijk zal worden dat enkel de diagonalen van de matrix een rol spelen.

We vertrekken daartoe van de “positieve” 2x2 operatoren die we kunnen afbeelden op een van de niet ingebedde punten van het een onderscheidingen universum

Hieruit blijkt dat we de bitstring voor <<>> en voor a kunnen herkennen, ofwel in de linksboven/rechtsonder diagonaal, ofwel in de rechtsboven/linksonder diagonaal.

Uiteraard ligt het voor de hand dit patroon uit te breiden naar hogere universa. Hierbij blijkt dat de matrix vermenigvuldiging leidt tot een nieuwe symmetriebreking die op zijn eigenschappen zal moeten onderzocht worden.

Linksboven/rechtsonder diagonaal

We beelden de punten van het twee onderscheidingen universum af op diagonale operatoren.

Het kwadraat van de operatoren is de positieve eenheid.

Sommeren van de basis operatoren levert de operatoren waarop de andere punten van het twee onderscheidingen universum afgebeeld kunnen worden.

Bijvoorbeeld: <<a><b>> wordt afgebeeld op de vectorsom <>⊕<a>⊕<b>⊕a•b die dan afgebeeld wordt op de 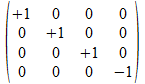operator . Het kwadraat van deze operatoren is terug de eenheid operator.

Het is duidelijk dat deze afbeelding zonder problemen verder kan uitgebreid worden voor hogere universa: alle betekende cellen van de matrix kunnen zich enkel maar op de linksboven/rechtsonder diagonaal bevinden.

Rechtsboven/linksonder diagonaal

Het kwadraat van de operatoren is ofwel de positieve eenheid, ofwel de negatieve eenheid. We merken ook op dat de vermenigvuldiging van twee rechtsboven/linksonder operatoren aanleiding geeft tot een linksboven/rechtsonder operator, de vermenigvuldiging van een rechtsboven/linksonder operator met een linksboven/rechtsonder operator (of omgekeerd) resulteert in een rechtsboven/linksonder operator. Dat betekent ook dat vermenigvuldiging met de operator waarop we <<>> afgebeeld hebben een rechtsboven/linksonder operator zal afbeelden op zijn linksboven/rechtsonder variant.

Dit zijn allemaal argumenten op de volgende gemengde afbeelding van diagonale operatoren uit te voeren, waarbij de eenheid operator overeenkomt met de eenheid operator van de gewone vector vermenigvuldiging.

Gemengde diagonale operatoren

Merk op dat we de afbeelding voor a•b veranderd hebben naar zijn inbedding. Dit is gemotiveerd door de matrix vermenigvuldiging van de operator voor <a•b> met de operator voor b die dan de operator voor <a> geeft, volledig overeenkomstig de vector vermenigvuldiging van beide. Nochtans is de overeenkomst met de vector vermenigvuldiging niet volledig door te trekken. Immers: sommeren van de basis operatoren levert de operatoren waarop de andere punten van het twee onderscheidingen universum afgebeeld kunnen worden. Nemen we nu als voorbeeld: <<a><b>>, dit wordt afgebeeld op de vectorsom <>⊕<a>⊕<b>⊕a•b die dan afgebeeld wordt op de operator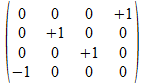. Het kwadraat van deze operator is dan 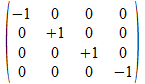, namelijk de afbeelding van <a•b>, en dus niet de eenheid operator. De vierde macht zal echter wel de eenheid operator opleveren.

Merk op dat de anderduale vectoren, ook bij uitbreidingen naar nog hogere universa, altijd zullen afgebeeld worden op linksboven/rechtsonder operatoren, en de zelfduale vectoren altijd zullen afgebeeld worden op rechtsboven/linksonder operatoren, overeenkomstig de eigenschap dat het product van twee zelfduale vectoren een andersduale vector geeft, evenzeer het product van twee andersduale vectoren een andersduale vector geeft, maar het product van een zelfduale met een andersduale vector een zelfduale vector geeft.

Besluit

Uitbreiding van het 1-splitsing universum kan de bitstring representatie van het haakformalisme reconstrueren met als verbindende operatie de matrix vermenigvuldiging. Maar het 1-splitsing universum uitbreiden zoals hier voorgesteld werd geeft ook aanleiding tot nieuwe representaties die een linksboven/rechtsonder diagonaal stellen tegenover een rechtsboven/linksonder diagonaal, waarbij andere eigenschappen ontstaan die nog verder kunnen onderzocht worden.