Een nevenschikking xy in het haakformalisme kan met de som operatie ⊕ en de reeds gedefinieerde product operatie • voorgesteld worden door: <<>>⊕<x>⊕<y>⊕<x•y>, wat we de haakvector vorm van de nevenschikking kunnen noemen.

We kunnen dat met de volgende tabel illustreren die alle mogelijke ervaringswaarden van x en y lijst, de vaste waarde (namelijk +1) van <<>> en de berekende waarden van de andere termen:

Deze tabel is één-op-één af te beelden op de overeenkomstige tabel die de waarden van de haaknevenschikking xy geeft.

De inbedding van een nevenschikking, bijvoorbeeld <xy>, kan uitgedrukt worden door elke vectorcomponent in te bedden. <xy> wordt dan in vectorvertaling <>⊕x⊕y⊕x•y.

Dit kan naar universa met meer dan twee onderscheidingen uitgebreid worden en blijft perfect coherent. Een nevenschikking van twee of meer punten blijkt dus als een som van de optredende punten en hun product(en) geschreven te kunnen worden wanneer we deze punten en producten als vectoren interpreteren. Zo kunnen alle haakuitdrukkingen in vectorvorm vertaald worden. Deze uitdrukking is geldig voor alle mogelijke invullingen van x en y. Al deze uitspraken kunnen gemakkelijk gecheckt worden door toepassing van de stellingen van het haakformalisme.

De waarden <> en <<>> zullen we scalair noemen.

Enkelvoudige onderscheidingen en hun inbedding zullen we (1-)vectoren noemen.

Transformaties en hun inbedding zullen 2-vectoren, 3-vectoren enz... noemen.

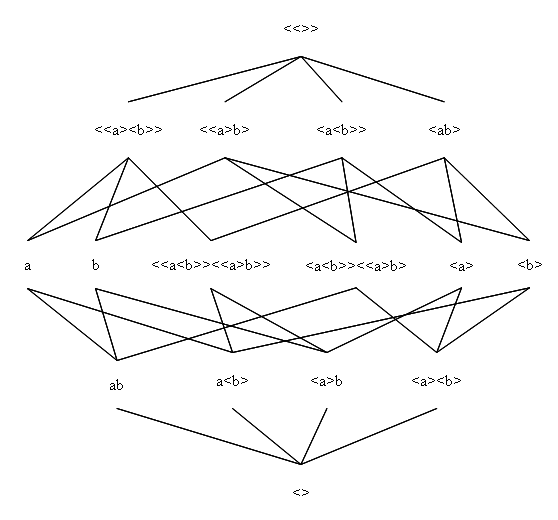
De tralie van een twee-onderscheidingen universum is hierbij gegeven in een tabelvorm die de tralievorm in onderstaande afbeelding vormelijk herneemt.

Hieronder geven we de vertalingen per niveau

Niveau 4

Niveau 3

Niveau 2

Niveau 1

Niveau 0

Elk punt in een twee-onderscheidingen universum is uit te drukken als de som van een scalair, vectoren en de enige 2-vector en hun inbeddingen. Dit is hierboven aangetoond. Elk punt in een drie-onderscheidingen universum is uit te drukken als de som van een scalair, vectoren, 2-vectoren en de enige 3-vector en hun inbeddingen. De volledige lijst tonen we hier.

Elk punt in een n-onderscheidingen universum is uit te drukken als de som van een scalair, vectoren, 2-vectoren, 3-vectoren, 4-vectoren, …, n-vectoren enz... en hun inbeddingen. Een volledige lijst construeren zou volledig kunnen geautomatiseerd worden. De scalair, vectoren, 2-vectoren, 3-vectoren, 4-vectoren enz... zijn de basisvectoren voor de constructie als vectorsom en we kunnen hun aantal onderzoeken. Zo kunnen we elke mogelijke welgevormde haakuitdrukking uitdrukken maar ook niet welgevormde haakuitdrukkingen (gecollapste haakuitdrukkingen).

De welgevormde haakuitdrukkingen kunnen we uitdrukken met enkel de operatie van nevenschikking en inbedding (in haakvorm). De welgevormde haakuitdrukkingen kunnen we nu ook als haakvector noteren met de operaties van inbedding, vectorsom en vectorproduct. Dit geeft dan ook de mogelijkheid om niet welgevormde haakuitdrukkingen te noteren. Dit maakt het mogelijk om de notaties uit te breiden waarin welgevormde en gecollapste uitdrukkingen kunnen voorkomen, want, indien nuttig, zouden we ook een hybride notatie kunnen ontwikkelen waarin we nevenschikking, vectorsom en vectorproduct met elkaar kunnen combineren door een dubbele haak te gebruiken. Zo kunnen we de welgevormde haakuitdrukking a noteren met haken als <<<>⊕<a>⊕<b>⊕a•b>><<<>⊕<a>⊕b⊕<a•b>>>, nevenschikking dus, overeenkomend met de nevenschikking <<a><b>><<a>b>, en dit is niet anders dan a.