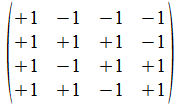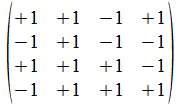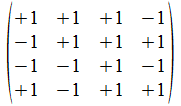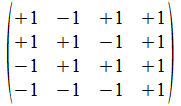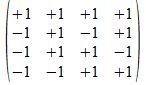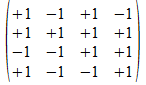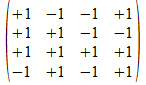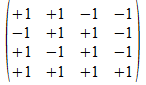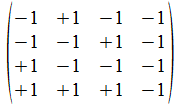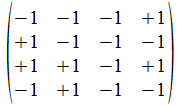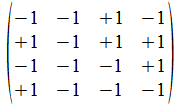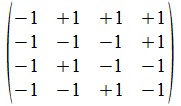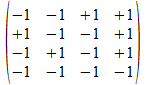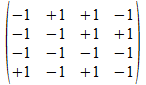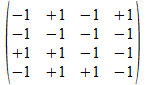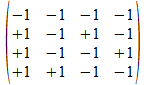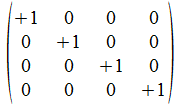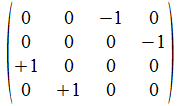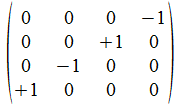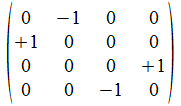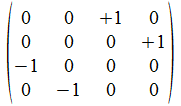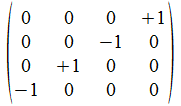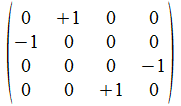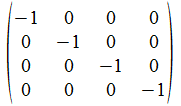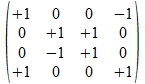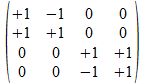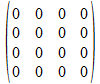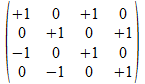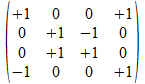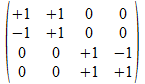Met de (som van de) operatoren van het 2-splitsing universum kunnen we willekeurige haakvectoren projecteren op de twee basissen van het twee-onderscheidingen universum: de basis gevormd door het centraal niveau en de extrema, en de basis gevormd door de atomen. Aangezien het twee-onderscheidingen universum alleen maar het centraal niveau, extrema en atomen kent zullen we dus kunnen projecteren op alle punten van het twee-onderscheidingen universum. Daarenboven kan elk punt van het twee-onderscheidingen universum zowel als een som van vectoren van centraal niveau en extrema uitgedrukt worden, als op als een som van atomen uitgedrukt worden.

We geven een voorbeeld met operatoren die voldoen aan de reverse regels van Hamilton. Merk op dat de transpose (invers) van de atomen de gecollapste vorm genereert, maar de ingebedde vorm voor de onderscheidingen.

Operatoren met de functie van atomen

Vier operatoren met de functie van OR-atomen

Som

1-j-k-i

1-j+k+i

1+j-k+i

1+j+k-i

Haakvector

<<>>⊕a⊕b⊕<a•b>

<<>>⊕a⊕<b>⊕a•b

<<>>⊕<a>⊕b⊕a•b

<<>>⊕<a>⊕<b>⊕<a•b>

Haakuitdrukking

<a><b>

<a>b

a<b>

ab

Signatuur string

---+

-+--

--+-

+---

Operator

Kolom basis

<<>>; <a>; <a•b>; <b>

a; <<>>; <b>; a•b

a•b; b; <<>>; <a>

b; <a•b>; a; <<>>

Rij basis

O1; A4; A2; A3

A3; O2; A4; A1

A4; A1; O3; A2

A2; A3; A1; O4

Transpose

1-(-j-k-i)

1-(-j+k+i)

1-(+j-k+i)

1-(+j+k-i)

Invers/transpose

Kolom basis

O1; A4; A2; A3

A3; O2; A4; A1

A4; A1; O3; A2

A2; A3; A1; O4

Rij basis

<<>>; <a>; <a•b>; <b>

a; <<>>; <b>; a•b

a•b; b; <<>>; <a>

b; <a•b>; a; <<>>

Signatuur string

xxx+

x+xx

xx+x

+xxx

Haakuitdrukking

<a><b>↔<<>>

<a>b↔<<>>

a<b>↔<<>>

ab↔<<>>

Haakvector

<<>>⊕<a>⊕<b>⊕a•b

<<>>⊕<a>⊕b⊕<a•b>

<<>>⊕a⊕<b>⊕<a•b>

<<>>⊕a⊕b⊕a•b

Vier operatoren de functie van AND-atomen

Som

-1-j-k+i

-1-j+k-i

-1+j-k-i

-1+j+k+i

Haakvector

<>⊕a⊕b⊕a•b

<>⊕a⊕<b>⊕<a•b>

<>⊕<a>⊕b⊕<a•b>

<>⊕<a>⊕<b>⊕a•b

Haakuitdrukking

<ab>

<a<b>>

<<a>b>

<<a><b>>

Signatuur string

-+++

++-+

+-++

+++-

Operator

Kolom basis

<b>; a•b; <a>; <>

<a•b>; <b>; <>; a

<a>; <>; b; <a•b>

<>; a; a•b; b

Rij basis

O2; O3; O1; A4

O4; O1; A3; O2

O3; A2; O4; O1

A1; O4; O2; O3

Transpose

-1-(-j-k+i)

-1-(-j+k-i)

-1-(+j-k-i)

-1-(+j+k+i)

Invers/transpose

Kolom basis

O2; O3; O1; A4

O4; O1; A3; O2

O3; A2; O4; O1

A1; O4; O2; O3

Rij basis

<b>; a•b; <a>; <>

<a•b>; <b>; <>; a

<a>; <>; b; <a•b>

<>; a; a•b; b

Signatuur string

-xxx

xx-x

x-xx

xxx-

Haakuitdrukking

<ab>↔<<>>

<a<b>>↔<<>>

<<a>b>↔<<>>

<<a><b>>↔<<>>

Haakvector

<>⊕<a>⊕<b>⊕<a•b>

<>⊕<a>⊕b⊕a•b

<>⊕a⊕<b>⊕a•b

<>⊕a⊕b⊕<a•b>

Operatoren met de functie van onderscheidingen

Som

1

-j

-k

-i

Operator

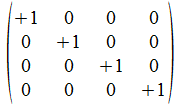
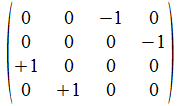
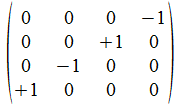
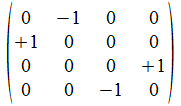
Kolom basis

(<>⊕A1); (<>⊕A2); (<>⊕A3); (<>⊕A4)

(<>⊕A3); (<>⊕A4); (<<>>⊕O1); (<<>>⊕O2)

(<>⊕A4); (<<>>⊕O3); (<>⊕A2); (<<>>⊕O1)

(<>⊕A2); (<<>>⊕O1); (<<>>⊕O4); (<>⊕A3)

Rij basis

(<>⊕A1); (<>⊕A2); (<>⊕A3); (<>⊕A4)

(<<>>⊕O3); (<<>>⊕O4); (<>⊕A1); (<>⊕A2)

(<<>>⊕O4); (<>⊕A3); (<<>>⊕O2); (<>⊕A1)

(<<>>⊕O2); (<>⊕A1); (<>⊕A4); (<<>>⊕O3)

Transpose

1

+j

+k

+i

Invers/transpose

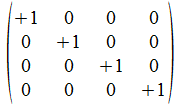
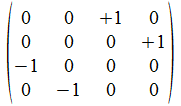
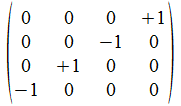
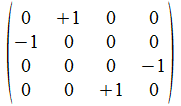
Kolom basis

(<>⊕A1); (<>⊕A2); (<>⊕A3); (<>⊕A4)

(<<>>⊕O3); (<<>>⊕O4); (<>⊕A1); (<>⊕A2)

(<<>>⊕O4); (<>⊕A3); (<<>>⊕O2); (<>⊕A1)

(<<>>⊕O2); (<>⊕A1); (<>⊕A4); (<<>>⊕O3)

Rij basis

(<>⊕A1); (<>⊕A2); (<>⊕A3); (<>⊕A4)

(<>⊕A3); (<>⊕A4); (<<>>⊕O1); (<<>>⊕O2)

(<>⊕A4); (<<>>⊕O3); (<>⊕A2); (<<>>⊕O1)

(<>⊕A2); (<<>>⊕O1); (<<>>⊕O4); (<>⊕A3)



Som

-1

+j

+k

+i

Operator

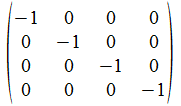
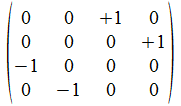
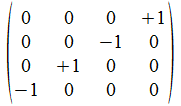
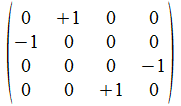
Kolom basis

(<<>>⊕O1); (<<>>⊕O2); (<<>>⊕O3); (<<>>⊕O4)

(<<>>⊕O3); (<<>>⊕O4); (<>⊕A1); (<>⊕A2)

(<<>>⊕O4); (<>⊕A3); (<<>>⊕O2); (<>⊕A1)

(<<>>⊕O2); (<>⊕A1); (<>⊕A4); (<<>>⊕O3)

Rij basis

(<<>>⊕O1); (<<>>⊕O2); (<<>>⊕O3); (<<>>⊕O4)

(<>⊕A3); (<>⊕A4); (<<>>⊕O1); (<<>>⊕O2)

(<>⊕A4); (<<>>⊕O3); (<>⊕A2); (<<>>⊕O1)

(<>⊕A2); (<<>>⊕O1); (<<>>⊕O4); (<>⊕A3)

Transpose

-1

-j

-k

-i

Invers/transpose

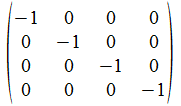
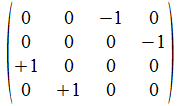
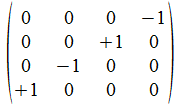
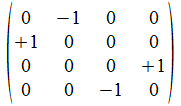
Kolom basis

(<<>>⊕O1); (<<>>⊕O2); (<<>>⊕O3); (<<>>⊕O4)

(<>⊕A3); (<>⊕A4); (<<>>⊕O1); (<<>>⊕O2)

(<>⊕A4); (<<>>⊕O3); (<>⊕A2); (<<>>⊕O1)

(<>⊕A2); (<<>>⊕O1); (<<>>⊕O4); (<>⊕A3)

Rij basis

(<<>>⊕O1); (<<>>⊕O2); (<<>>⊕O3); (<<>>⊕O4)

(<<>>⊕O3); (<<>>⊕O4); (<>⊕A1); (<>⊕A2)

(<<>>⊕O4); (<>⊕A3); (<<>>⊕O2); (<>⊕A1)

(<<>>⊕O2); (<>⊕A1); (<>⊕A4); (<<>>⊕O3)

De gecollapste vormen worden dan gegenereerd door gecollapste vectoren op centraal niveau, merk op hoe de extrema zich hierbij afscheiden omdat het invers/transpose patroon hierbij niet van toepassing is.

Som

1+1

1-j

1-k

1-i

Operator

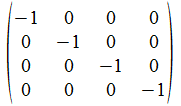
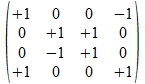
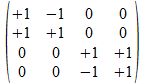
Kolom basis

(<<>>⊕O1); (<<>>⊕O2); (<<>>⊕O3); (<<>>⊕O4)

(<>⊕<a>); (<>⊕a); (b⊕a•b); (b⊕<a•b>)

(<>⊕<a•b>); (a⊕<b>); (<>⊕a•b); (a⊕b)

(<>⊕<b>); (a⊕a•b); (<a>⊕a•b); (<>⊕b)

Rij basis

(<<>>⊕O1); (<<>>⊕O2); (<<>>⊕O3); (<<>>⊕O4)

(<b>⊕<a•b>); (<b>⊕a•b); (<>⊕<a>); (<>⊕a)

(<a>⊕<b>); (<>⊕a•b); (<a>⊕b); (<>⊕<a•b>)

(<a>⊕<a•b>); (<>⊕<b>); (<>⊕b); (a⊕<a•b>)

Transpose

1-1

1+j

1+k

1+i

Invers/transpose

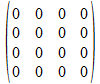
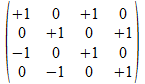
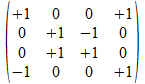
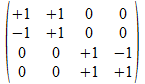
Kolom basis

0; 0; 0; 0

(<b>⊕<a•b>); (<b>⊕a•b); (<>⊕<a>); (<>⊕a)

(<a>⊕<b>); (<>⊕a•b); (<a>⊕b); (<>⊕<a•b>)

(<a>⊕<a•b>); (<>⊕<b>); (<>⊕b); (a⊕<a•b>)

Rij basis

0; 0; 0; 0

(<>⊕<a>); (<>⊕a); (b⊕a•b); (b⊕<a•b>)

(<>⊕<a•b>); (a⊕<b>); (<>⊕a•b); (a⊕b)

(<>⊕<b>); (a⊕a•b); (<a>⊕a•b); (<>⊕b)