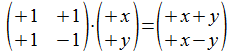
We kunnen nu wat bekend is van de Hadamard matrices in herinnering brengen, waarbij we de resultaten kunnen bestuderen uit wat reeds bekend is van haakvectorsommen. We zullen hiertoe willekeurige haakvectoren noteren als x, y, z of x₀, x₁, x₂ enz... Die haakvectoren hoeven niet welgevormd te zijn.

De actie van de Hadamard matrix H₂ op twee haakvectoren kan dan als volgt bestudeerd worden.

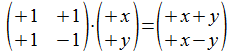
De vermenigvuldigingen en sommen zijn modulo3, waarbij we de conventie aannemen dat het minteken staat voor een som met een ingebedde haakvector. Het is duidelijk dat in matrix formaat +1 staat voor <<>>.

De actie van H₂ is goed gedefinieerd, wat ook het universum zou zijn waarin x en y zouden uitgedrukt worden: het resultaat zal een kolomvector zijn met componenten uit éénzelfde overkoepelend universum. Dat is juist de kracht van deze voorstelling: twee willekeurige haakvectoren krijgen een plaats in eenzelfde universum.

Bij de inverse transformatie wordt het ingebedde punt bekomen.

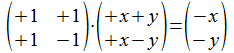
Indien men een klassieke som wil gebruiken is er voor de inverse operatie een normalisatiefactor nodig, die voor H₂ gelijk is aan 2^-1.

Het kwadraat van H₂ is de negatieve eenheidsmatrix, dus een kwadraat dat overeenkomt met de actie van de imaginaire i.

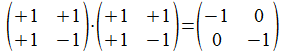
De methode van Sylvester laat nu toe om natuurlijk geordende Hadamard matrices te bouwen van orde 2ⁿ voor elk niet-negatief geheel getal n, of dus matrices van de orde 1, 2, 4, 8, 16, enz…

Voor H₂ is n=1 en voor H₁ = (+) is de orde gelijk aan 2⁰ = 1

Karakteristiek voor deze matrices is dat de elementen in de eerste rij en de eerste kolom allemaal positief en gelijk aan +1 zijn. De elementen in de andere rijen en kolommen zijn gelijk verdeeld tussen +1 en –1 waarden. Hadamard matrices zijn symmetrisch, wat betekent dat ze vierkant zijn en gelijk aan hun transpose matrix. Deze symmetrieën kunnen we perfect afleiden uit het haakformalisme. Het spoor van een Hadamard matrix is altijd nul.

In het algemeen zal gelden dat H_m met m=2ⁿ een willekeurige haakvector die uitgedrukt wordt als een kolomvector (rijvector), met eventueel componenten uit verschillende gecollapste ruimten, zal transformeren naar een vector uit de kolom-ruimte (rij-ruimte) van één onderscheidingen universum: het n onderscheidingen universum waarvan men kiest dat het met de basis van H_m moet kunnen uitgedrukt worden.