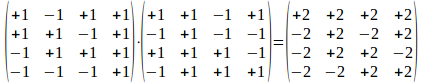
We tonen aan dat rotaties van haakuitdrukkingen kunnen geïnterpreteerd worden als een modulo3 operatie.

Wanneer we k<j> roteren met behulp van <k><j> dan rekenen we (<k><j>)(k<j>)(<k><j>)^-1 uit.

We doen dat in twee stappen, eerst (<k><j>)(k<j>):

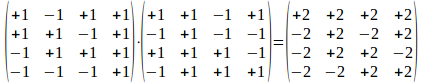
Het invers van (<k><j>) is

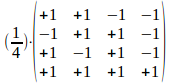
en dus

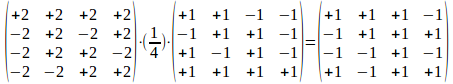
en we merken dat dit niet anders is dan <k>j, en dat zowel in modulo3 formaat als in getalformaat (waarbij dus normalisaties met het invers uitgevoerd worden). Dus (<k><j>)(k<j>)(<k><j>)^-1=<k>j. Ondanks het feit dat de tussenstap geen welgevormde haakuitdrukking modelleert gaan we met de hele operatie van rotatie van een welgevormde haakuitdrukking naar een welgevormde haakuitdrukking. Rotatie introduceert blijkbaar ook een modulo3 operatie.

Patroon: k<j> roteren met <k><j> geeft <k>j

Patroon: <k><j> roteren met k<j> geeft kj

We geven nog een voorbeeld van een rotatie van een atoom niveau met als rotor een punt op centraal niveau, we roteren nu <k><j> met behulp van <k>, we vormen dus (<k>)(<k><j>)(<k>)^-1 en we krijgen k<j>.

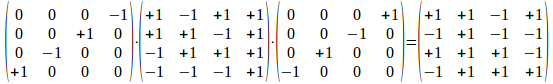
Patroon: <k><j> roteren met <k> geeft k<j>

Patroon: <k> roteren met <k><j> geeft <j>