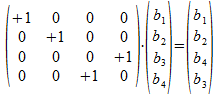
Quantum gates zijn operatoren die kwantum toestanden als kolomvectoren transformeren in een nieuwe kwantum toestand op een reversibele manier. Dit betekent dat de omgekeerde transformatie uitgevoerd moet worden door de transpose van de operator, waardoor dus de vermenigvuldiging van de beide operatoren de eenheidsoperator geeft. Bij de drie voorbeelden die hieronder gegeven worden (CNOT, CCNOT en CSWAP) zijn de operatoren en hun transpose zelfs identiek en er kan gecontroleerd worden dat het kwadraat van de operatoren gelijk is aan de eenheidsoperator.
De laatst toegevoegde onderscheiding ℵ wordt bij kwantum gates gemodelleerd door wat men een “control bit” noemt. Het is die qubit die gemeten wordt en bij de meting de bedoelde collaps realiseert.
De CNOT gate is de operator
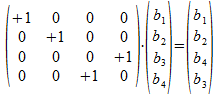
Inwerkend op de basisvectoren van het twee-qubit universum wordt de volgende transformatie uitgevoerd:
Korte notatie |
Kolomvector notatie |
Getransformeerde vector |
Getransformeerde kolomvector |
|00> |
(1 0 0 0)T |
|00> |
(1 0 0 0)T |
|01> |
(0 1 0 0)T |
|01> |
(0 1 0 0)T |
|10> |
(0 0 1 0)T |
|11> |
(0 0 0 1)T |
|11> |
(0 0 0 1)T |
|10> |
(0 0 1 0)T |
Noemen we de eerste qubit b1 en de tweede qubit b2, waarbij we |b1b2> vormen, dan kunnen we ook de tabel opbouwen
b1 |
b2 |
b1 |
b1XORb2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
De CNOT gate gaat dus |b1b2> transformeren in |b1(b1XORb2)>
De kolomvectoren b1 en b2 worden beschouwd als input, de kolomvectoren b2 en b1XORb2 worden beschouwd als output. De CNOT gate wordt als volgt geïnterpreteerd: in het geval dat b1 niet kan onderscheiden worden van 1 is de output de negatie van b2. Wat in de gereduceerde tabel als volgt kan getoond worden:
b1 |
b2 |
b1 |
b1XORb2 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
We zullen nu onderzoeken vanuit welke welgevormde haakuitdrukkingen deze collaps kan afgeleid worden. We vertalen daartoe het bitmodel in het haakmodel (OR en AND worden omgewisseld en XOR en XNOR worden omgewisseld). Dus b1XORb2 wordt vertaald als <<b1<b2>><<b1>b2>> in welgevormde uitdrukking en we stellen vast dat <<b1<b2>><<b1>b2>> overeenkomt met een output van de CNOT operator op voorwaarde dat de andere output b1↔<<>>.
Dus b1 controleert. Heeft b1 waarde <>, dan is de output b2, heeft b1 waarde <<>>, dan is de output <b2>. Dat is eenduidig en reversibel. <<b1<b2>><<b1>b2>> kunnen we ook schrijven als <b1b2><<b1><b2>> en dit is niet anders dan het creatief product (<b2>⊗b2)b1.
De CCNOT gate is de operator
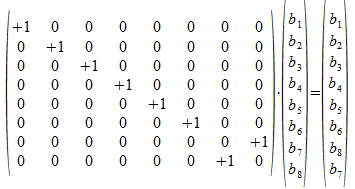
Inwerkend op de basisvectoren van het drie-qubit universum wordt de volgende transformatie uitgevoerd:
Korte notatie |
Kolomvector notatie |
Getransformeerde vector |
Getransformeerde kolomvector |
|000> |
(1 0 0 0 0 0 0 0)T |
|000> |
(1 0 0 0 0 0 0 0)T |
|001> |
(0 1 0 0 0 0 0 0)T |
|001> |
(0 1 0 0 0 0 0 0)T |
|010> |
(0 0 1 0 0 0 0 0)T |
|010> |
(0 0 1 0 0 0 0 0)T |
|011> |
(0 0 0 1 0 0 0 0)T |
|011> |
(0 0 0 1 0 0 0 0)T |
|100> |
(0 0 0 0 1 0 0 0)T |
|100> |
(0 0 0 0 1 0 0 0)T |
|101> |
(0 0 0 0 0 1 0 0)T |
|101> |
(0 0 0 0 0 1 0 0)T |
|110> |
(0 0 0 0 0 0 1 0)T |
|111> |
(0 0 0 0 0 0 0 1)T |
|111> |
(0 0 0 0 0 0 0 1)T |
|110> |
(0 0 0 0 0 0 1 0)T |
Noemen we de eerste bit b1, de tweede bit b2, de derde bit b3 waarbij we |b1b2b3> vormen, dan kunnen we ook de tabel opbouwen
b1 |
b2 |
b3 |
b1 |
b2 |
(b1ANDb2)XORb3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
De CCNOT gate gaat dus |b1b2b3> transformeren in |b1b2((b1ANDb2)XORb3)>
We zullen nu onderzoeken vanuit welke welgevormde haakuitdrukkingen deze collaps kan afgeleid worden. We vertalen daartoe het bitmodel in het haakmodel (OR en AND worden omgewisseld en XOR en XNOR worden omgewisseld). Dus (b1ANDb2)XORb3 wordt vertaald als <<b1b2<b3>><<b1b2>b3>> in welgevormde uitdrukking en we stellen vast dat <<b1b2<b3>><<b1b2>b3>> overeenkomt met de CCNOT operator wanneer zowel b1 ↔<<>> als b2 ↔<<>> zoals in de tabel hieronder bewezen wordt.
b1 |
b2 |
b3 |
<<b1b2<b3>><<b1b2>b3>> |
<<>> |
<<>> |
<> |
<<>> |
<<>> |
<<>> |
<<>> |
<> |
Dus b1b2 controleert. Heeft b1b2 waarde <>, dan is de output b3, heeft b1b2 waarde <<>>, dan is de output <b3>. Dat is eenduidig en reversibel. <<b1b2<b3>><<b1b2>b3>> kunnen we ook schrijven als <b1b2b3><<b1b2><b3>> en dit is niet anders dan het creatief product (<b3>⊗b3)b1b2.
De CSWAP gate is de operator
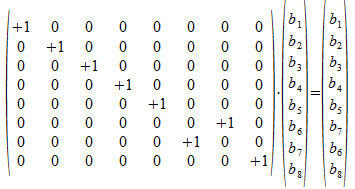
Inwerkend op de basisvectoren van het drie-qubit universum wordt de volgende transformatie uitgevoerd:
Korte notatie |
Kolomvector notatie |
Getransformeerde vector |
Getransformeerde kolomvector |
|000> |
(1 0 0 0 0 0 0 0)T |
|000> |
(1 0 0 0 0 0 0 0)T |
|001> |
(0 1 0 0 0 0 0 0)T |
|001> |
(0 1 0 0 0 0 0 0)T |
|010> |
(0 0 1 0 0 0 0 0)T |
|010> |
(0 0 1 0 0 0 0 0)T |
|011> |
(0 0 0 1 0 0 0 0)T |
|011> |
(0 0 0 1 0 0 0 0)T |
|100> |
(0 0 0 0 1 0 0 0)T |
|100> |
(0 0 0 0 1 0 0 0)T |
|101> |
(0 0 0 0 0 1 0 0)T |
|110> |
(0 0 0 0 0 0 1 0)T |
|110> |
(0 0 0 0 0 0 1 0)T |
|101> |
(0 0 0 0 0 1 0 0)T |
|111> |
(0 0 0 0 0 0 0 1)T |
|111> |
(0 0 0 0 0 0 0 1)T |
Noemen we de eerste bit b1, de tweede bit b2, de derde bit b3 waarbij we |b1b2b3> vormen, dan kunnen we ook de tabel opbouwen
b1 |
b2 |
b3 |
b1 |
(NOTb1ANDb2)XOR(b1ANDb3) |
(b1ANDb2)XOR(NOTb1ANDb3) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
De CSWAP gate gaat dus |b1b2b3> transformeren in |b1((NOTb1ANDb2)XOR(b1ANDb3))((b1ANDb2)XOR(NOTb1ANDb3))>
We zullen nu onderzoeken vanuit welke welgevormde haakuitdrukkingen deze beide outputs kunnen afgeleid worden. We vertalen daartoe het bitmodel in het haakmodel (OR en AND worden omgewisseld en XOR en XNOR worden omgewisseld, merk op dat in dit geval XOR niet verschillend is van OR en dus XNOR evenmin verschillend is van AND)
(NOTb1ANDb2)XOR(b1ANDb3) |
<<<b1>b2><b1b3>> |
(b1ANDb2)XOR(NOTb1ANDb3) |
<<b1b2><<b1>b3>> |
Een volledige constructie van de tabel toont aan dat de collaps van b1 ↔<<>> inderdaad een swap van de waarden van b2 en b3 uitvoert.
b1 |
b2 |
b3 |
<<<b1>b2><b1b3>> |
<<b1b2 ><<b1>b3>> |
<<>> |
<> |
<> |
<> |
<> |
<<>> |
<> |
<<>> |
<<>> |
<> |
<<>> |
<<>> |
<> |
<> |
<<>> |
<<>> |
<<>> |
<<>> |
<<>> |
<<>> |
<<<b1>b2><b1b3>> schrijven we als <b1<b3>><<b1><b2>> en dus het creatief product (b3⊗b2)b1. Heeft b1 waarde <> dan heeft (b3⊗b2)b1 waarde van b2. Heeft b1 waarde <<>> dan heeft (b3⊗b2)b1 waarde van b3.
<<b1b2><<b1>b3>> schrijven we als <b1<b2>><<b1><b3>> en dus het creatief product (b2⊗b3)b1. Heeft b1 waarde <> dan heeft (b2⊗b3)b1 waarde van b3. Heeft b1 waarde <<>> dan heeft (b2⊗b3)b1 waarde van b2.
Er werd aangetoond dat het inzetten van de CNOT en CCNOT, ofwel het inzetten van de CNOT en CSWAP voldoende is om alle bekende klassieke berekeningen in het kwantum formalisme te realiseren.
Maar zoals in het haakformalisme duidelijk wordt: dit heeft alles te maken met de reversibiliteit van het creatief product. Dit is niet exclusief verbonden aan de fysische realisatie ervan.