Om gebeurtenissen te leren kennen die men wel kan bedenken en dus kan verwachten, waarvoor men enerzijds niet kan kiezen en die men anderzijds wel kan laten gebeuren, zal men “hetzelfde” verschillende malen proberen te ervaren. De afwijkingen die dan relevant zijn (die het agens als relevant beoordeelt) zullen het agens leren hoe “hetzelfde” dan wel moet omschreven worden, dus welk model het agens ter beschikking heeft of kan construeren om van dezelfde gebeurtenissen te kunnen spreken. Dat een gebeurtenis als dezelfde gecatalogiseerd wordt is dus een zeer abstract begrip dat voornamelijk te maken heeft met de creativiteit, mogelijkheden en beperkingen van het agens. Het haakformalisme maakt het mogelijk deze a priori te expliciteren.
Een klassieke illustratie hiervan is de paradox van Bertrand (Joseph Bertrand Calcul des probabilités 1889).
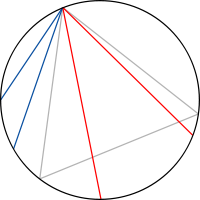
Bertrand stelt het volgende, op het eerste gezicht duidelijk geformuleerde probleem: beschouw een gelijkzijdige driehoek en zijn omschreven cirkel. Wat is de kans dat een willekeurig gekozen koorde van de cirkel groter is dan de zijde van de driehoek? Bertrand gaf dan drie oplossingsmethoden voor het probleem, die alle drie een andere uitkomst geven.
Kies een eerste punt op de cirkel en draai de cirkel zo dat een hoekpunt van de driehoek samenvalt met dit punt. Kies weer willekeurig een ander punt op de cirkel en teken de koorde tussen de twee punten. Alleen wanneer het tweede punt ligt op de boog tussen de twee andere hoekpunten van de driehoek, is de koorde langer dan de zijde van de driehoek. De lengte van deze boog is een derde van de gehele omtrek. De gevraagde kans is daarom 1/3.

Kies een straal van de cirkel, en kies een punt op deze straal, deze keuze bepaalt een unieke koorde door dit punt en loodrecht op deze straal. Draai nu de cirkel zo dat een zijde van de driehoek de straal loodrecht snijdt. Merk op dat deze zijde dan een middelloodlijn is van de straal. De gekozen koorde is alleen langer als het gekozen punt dichter ligt bij het middelpunt van de cirkel dan bij de rand. De gevraagde kans is daarom 1/2.

Kies een punt in het binnenste van de cirkel en neem de (unieke) koorde die dit punt als middelpunt heeft. Beschouw nu de ingeschreven cirkel van de gegeven gelijkzijdige driehoek. De oppervlakte van deze ingeschreven cirkel is een vierde van de oppervlakte van de omschreven cirkel. De koorde die we hebben geconstrueerd is alleen langer dan de zijde van de driehoek, als het midden binnen de ingeschreven cirkel ligt. De gevraagde kans is dus 1/4.
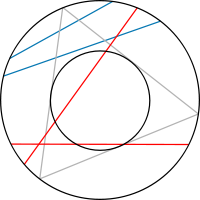
De vraag wat nu de “echte”, de “ware” waarschijnlijkheid is, is niet te beantwoorden omdat de werkelijkheid zich context-afhankelijk zal organiseren. De paradox van Bertrand toont duidelijk aan dat “hetzelfde” afhankelijk is van de manier waarop men de werkelijkheid bevraagt. Immers: wanneer men deze drie verschillende modellen om het probleem aan te pakken in de werkelijkheid door een fysisch proces modelleert, dan vindt men inderdaad ook empirisch (dus in werkelijkheid) de verschillen in kans terug. Dit betekent dat de willekeurige variabele niet enkel een theoretisch creatieve vondst is, maar evenzeer een praktisch te realiseren creatieve vondst. Elke creatief gevonden procedure om de beschouwde willekeurige variabele te construeren leidt tot een ander resultaat omdat men een andere onderscheiding als variabele meet en dus een andere entiteit. De willekeurige eindpunten methode gaat er van uit dat men een even waarschijnlijke (met andere woorden: een uniforme) verdeling beschouwt op een deel van de omtrek van de cirkel, de willekeurige straal methode gaat uit van een even waarschijnlijke verdeling op een straal van de cirkel, en de methode van het willekeurige midden gaat uit van een even waarschijnlijke verdeling op een deel van het oppervlak van de cirkel. Hoewel de klassieke wiskunde ervan uitgaat dat deze drie entiteiten een oneindig aantal punten hebben, toch zijn het andere entiteiten die gecreëerd worden en in werkelijkheid tot andere resultaten leiden. De even waarschijnlijke verdeling op een deel van de omtrek van de cirkel, op een straal van de cirkel, en op een deel van het oppervlak van de cirkel zijn andere verdelingen, even waarschijnlijk in hun eigen context maar niet even waarschijnlijk in elkaars context.
Dit is volledig analoog met het voorbeeld van een dobbelsteen waarbij men verschillende aspecten van die dobbelsteen in zijn context als willekeurige variabele zal beschouwen.