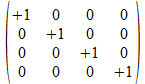
![]()
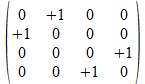
![]()
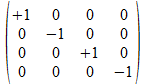
![]()
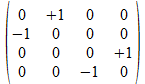
![]()
![]()
![]()
![]()
![]()
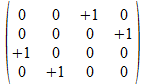
![]()
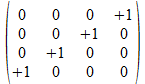
![]()
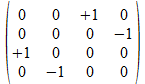
![]()

![]()
![]()
![]()
![]()
![]()
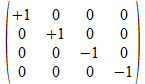
![]()
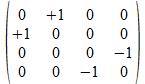
![]()
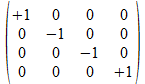
![]()
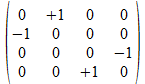
![]()
![]()
![]()
![]()
![]()

![]()
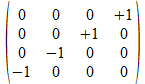
![]()
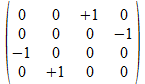
![]()
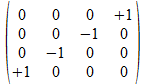
![]()
![]()
![]()
![]()
![]()
We zullen operatoren isomorfismen in het twee onderscheidingen universum construeren door de 4x4 operatoren af te beelden op kolom matrices of rij matrices zoals aangegeven in de tabel hieronder voor de 16 4x4 operatoren, met de kolom matrix rechts van de operator en de rij matrix onder de operator.
Met blauwe achtergrond zijn de operatoren aangegeven waarvan de kolom matrix en de rij matrix elkaar ingebedde transpose zijn. Het zijn die operatoren waarvan het kwadraat de negatieve eenheidsoperator is.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We kunnen nu de acht groepen operatoren afbeelden op bitstrings die basisvectoren van het twee onderscheidingen universum representeren. De afbeeldingen zijn onder de operator aangegeven. Het valt hierbij op dat de rekenregels die gelden voor de welgevormde haakuitdrukkingen niet gelden voor de matrices, inderdaad: het matrix product is niet commutatief en daarentegen is het haakvector product wel commutatief.
|
1 |
i |
j |
k |
|
|
|
|
|
|
<<>> |
<a> |
<b•a> |
<b> |
|
|
|
|
|
|
<<>> |
<<>> |
<b> |
<<>> |
|
|
|
|
|
|
<<>> |
<<>> |
<<>> |
<a> |
|
|
|
|
|
|
<<>> |
<b•a> |
<<>> |
<<>> |
Enkel de eerste afbeelding genereert alle basisvectoren van het twee onderscheidingen universum.
|
1 |
i |
j |
k |
|
|
|
|
|
|
<<>> |
<b•a> |
<b> |
<a> |
|
|
|
|
|
|
<<>> |
<a> |
a |
b•a |
|
|
|
|
|
|
<<>> |
b |
a |
<b> |
|
|
|
|
|
|
<<>> |
b |
<b•a> |
b•a |
Enkel de eerste afbeelding genereert alle basisvectoren van het twee onderscheidingen universum.