Onderscheiding
Operator naam
Operator matrix
<<>>
1
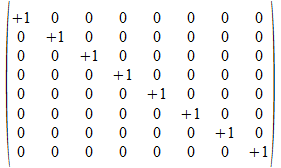
<>
-1
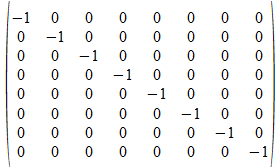
<b>
e1
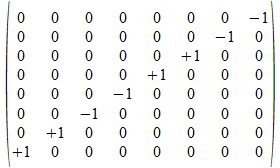
b
-e1
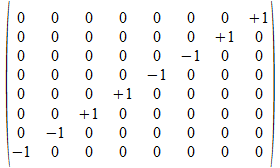
<c>
e2
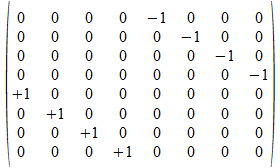
c
-e2
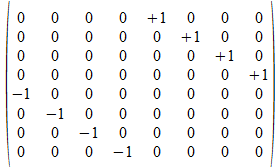
<c•b•a>
e3
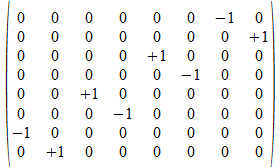
c•b•a
-e3
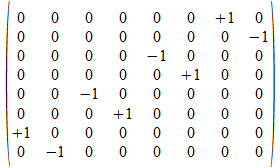
<c•b>
e4
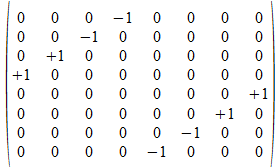
c•b
-e4
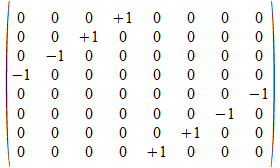
<b•a>
e5
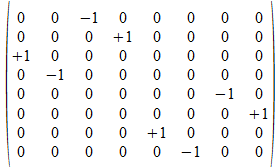
b•a
-e5
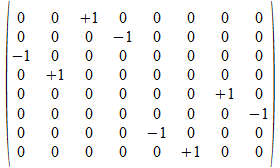
<a>
e6
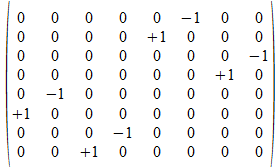
a
-e6
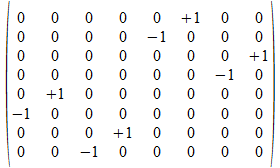
<c•a>
e7
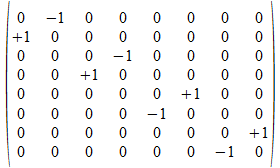
c•a
-e7
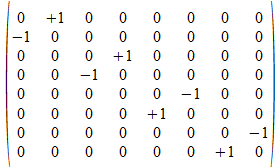
Sommige punten van het drie onderscheidingen universum kunnen op een 2 splitsing universum afgebeeld worden met behulp van matrices, maar dat is niet voor alle punten mogelijk. Het 3 splitsing universum heeft voldoende onderscheidende kracht om een matrix isomorfisme van het volledig drie onderscheidingen universum uit te voeren.
We voeren de volgende afbeelding uit:
|
Onderscheiding |
Operator naam |
Operator matrix |
|
<<>> |
1 |
|
|
<> |
-1 |
|
|
<b> |
e1 |
|
|
b |
-e1 |
|
|
<c> |
e2 |
|
|
c |
-e2 |
|
|
<c•b•a> |
e3 |
|
|
c•b•a |
-e3 |
|
|
<c•b> |
e4 |
|
|
c•b |
-e4 |
|
|
<b•a> |
e5 |
|
|
b•a |
-e5 |
|
|
<a> |
e6 |
|
|
a |
-e6 |
|
|
<c•a> |
e7 |
|
|
c•a |
-e7 |
|
We rekenen nu de volgende tabel van gecollapste atomen uit die voldoende zijn om de hele tralie op te spannen door geschikte sommen te maken:
|
Bitstring |
Drie-onderscheidingen haakvector |
Operator som |
Operator matrix |
|
+xxxxxxx |
<>⊕<a>⊕<b>⊕<c>⊕<b•a>⊕<b•c>⊕<c•a>⊕<c•b•a> |
-1+e1+e2+e3+e4+e5+e6+e7 |
|
|
x+xxxxxx |
<>⊕a⊕<b>⊕<c>⊕b•a⊕<b•c>⊕c•a⊕c•b•a |
-1+e1+e2-e3+e4-e5-e6-e7 |
|
|
xx+xxxxx |
<>⊕<a>⊕b⊕<c>⊕b•a⊕b•c⊕<c•a>⊕c•b•a |
-1-e1+e2-e3-e4-e5+e6+e7 |
|
|
xxx+xxxx |
<>⊕a⊕b⊕<c>⊕<b•a>⊕b•c⊕c•a⊕<c•b•a> |
-1-e1+e2+e3-e4+e5-e6-e7 |
|
|
xxxx+xxx |
<>⊕<a>⊕<b>⊕c⊕<b•a>⊕b•c⊕c•a⊕c•b•a |
-1+e1-e2-e3-e4+e5+e6-e7 |
|
|
xxxxx+xx |
<>⊕a⊕<b>⊕c⊕b•a⊕b•c⊕<c•a>⊕<c•b•a> |
-1+e1-e2+e3-e4-e5-e6+e7 |
|
|
xxxxxx+x |
<>⊕<a>⊕b⊕c⊕b•a⊕<b•c>⊕c•a⊕<c•b•a> |
-1-e1-e2+e3+e4-e5+e6-e7 |
|
|
xxxxxxx+ |
<>⊕a⊕b⊕c⊕<b•a>⊕<b•c>⊕<c•a>⊕c•b•a |
-1-e1-e2-e3+e4+e5-e6+e7 |
|
Als we nu overal +1 bijtellen dan vinden we de acht spoorloze matrices die de 8 AND-atomen van het drie onderscheidingen universum representeren, en waarvan de inbedding de 8 OR-atomen representeren.
Merk op dat alle e-operatoren, behalve e3 (en dus ook -e3) een transpose en invers hebben die de negatieve vorm is van de operator, zodanig dat het kwadraat niet kan onderscheiden kan worden van de -1 operator. De e3 operator echter is identiek met zijn transpose en invers en dus het kwadraat van deze operator kan niet onderscheiden worden van de 1 operator. Zo'n operator wordt in de klassieke definities een pseudoscalair genoemd.