Zeer veel belangrijke processen kunnen we modelleren door te veronderstellen dat ze veroorzaakt worden door een constante kracht of dus een constante versnelling. Zo kunnen we de vrije val van een object naar de aarde modelleren door te veronderstellen dat er een kracht werkzaam is die gegeven wordt door het product van massa en de lokale constante valversnelling g. Gegeven de snelheid v_t op het ogenblik t, dan wordt de snelheid op het ogenblik t' gegeven door v_t + a(t'-t), met a de lokale constante versnelling. De intensiteit van de snelheid (de intensiteit van de toestandsverandering in een proces) verandert dus op een spontane manier en dat willen we modelleren in het inzicht dat de intensiteit van een spontane verandering of spontane evolutie van (x-x₀) gegeven wordt door (x-x₀)(1+k)ⁿ. We stellen ons dan de vraag hoe k moet evolueren om het mogelijk te maken dat op elke tijdstap geldt dat (1+k)ⁿ=an. Noem nu (1+k)=x, dan moeten we de intensiteit van x zoeken zodanig dat xⁿ=an, dus x=(an)^1/n=e^ln(an)/n. De intensiteit is dus recht evenredig met een gewogen nde wortel uit n.

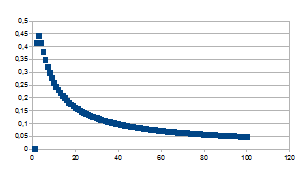
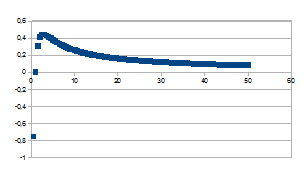
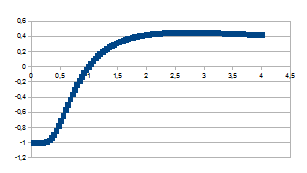
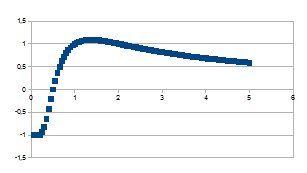
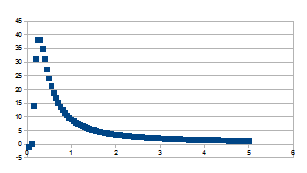
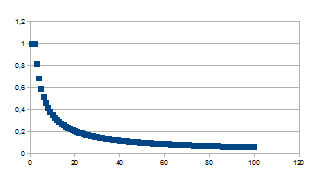
Wanneer we nu k of dus ((an)^1/n-1) uitzetten ten opzichte van n dan bekomen we de volgende grafieken die allemaal een snelle verandering tonen in de eerste tijdstappen, een piek bereiken en dan traag asymptotisch naderen naar nul bij grotere tijd. Hoe groter a, hoe hoger en scherper de piek.

Als we indachtig zijn dat, voor onbegrensde processen, k begrensd wordt tussen -1 en +1 dan zijn er maar een paar lijnen van de kolom die die werkelijkheid modelleren.

De verandering van k modelleert een verandering van waarnemingsresolutie in het haakformalisme, dus de verandering van “het minimale (maximale) verschil tussen twee waarneembare toestanden”. Voor processen waarin we het aantal tijdstappen zeer groot kunnen nemen is die verandering nagenoeg constant en neemt de snelheid van k traag af naar nul. Zoals we aantoonden modelleert een k=0 stabiliteit.

In de limiet, voor zeer grote n, geldt dan dat (1+0)ⁿ=an, dus a=1/n en de versnelling nadert dus ook tot nul. In de interpretatie van de constante versnelling door de aanwezigheid van massa (en dus zwaartekracht) betekent dit dat de waarnemingsresolutie voortdurend daalt en de zwaartekracht dus niet meer waarneembaar wordt. Dit kunnen we ook uitdrukken door te zeggen dat de ruimtelijke afstanden tussen massa's spontaan en onvermijdelijk groter wordt, wat een interpretatie is van het afnemen van de waarnemingsresolutie: de onmogelijkheid om nog elkaar uitsluitende toestanden te onderscheiden, een maximaal potentieel universum waarbij het toekennen van een ervaringswaarde (<> of <<>>) irrelevant geworden is.

Het proces van verandering van k wordt gekarakteriseerd door een initieel hoge piek, een proces dat een kandidaat is om de kosmische inflatie (een spontaan proces met zeer hoge versnelling en resulterend in een hoge maat van verandering) in de eerste fracties van een seconde na de big bang te verklaren. Merk op dat de waarnemingsresolutie inherent deel uitmaakt van deze beschrijving.