Veel gebruikte beslissingsheuristieken (bijvoorbeeld het gewogen gemiddelde) kunnen niet onderbouwd worden omdat ze enkel functioneren als alle waarderingen numeriek kunnen uitgedrukt worden. Er zijn maar weinig heuristieken die ook gebruikt kunnen worden voor ordinale waarderingen. We geven een fictief voorbeeld om de heuristieken te illustreren, waarbij de waarderingen van 7 oplossingen voor 4 aspecten in de volgende tabel gedocumenteerd worden:

Aspect A wordt numeriek gemeten (met niet geëxpliciteerde eenheid, bijvoorbeeld seconde, volt, euro,...), aspecten B en C worden ordinaal gemeten met verschillende waarderingen (bijvoorbeeld E staat voor excellent, G staat voor gewoon, Z staat voor zwak, H staat voor hoog) en aspect D wordt enkel nominaal gewaardeerd in twee categorieën, (bijvoorbeeld K staat voor klasse, O staat voor ordinair).

We merken op dat geen van de aspecten kan weggelaten worden en dat geen van de oplossingen een andere domineert. We moeten dus op zoek gaan naar een ordening die zo veel mogelijk op basis van de partiële ordeningsrelatie van het haakformalisme kan onderbouwd worden.

Ongewogen beslissingen

Meerderheidsregel

Met het beslissingscriterium van de meerderheidsregel beslist men dat i beter is dan j wanneer het aantal aspecten waarop i beter scoort dan j groter is dan het aantal aspecten waarop j beter scoort dan i. Aspecten worden hierbij als gelijkwaardig beschouwd, en het is die eenheid van gelijkwaardigheid die we kunnen optellen. Men behandelt aspecten hier dus als stemmers voor i of j waarbij elke stem even zwaar weegt. Deze methode werkt dus zuiver ordinaal, er kan dan ook geen rekening gehouden worden met de "afstand" tussen de verschillende oplossingen.

Uiteraard zijn hierbij paradoxen mogelijk doordat er geen transitiviteit geldt. Veronderstel drie aspecten waarbij de volgende volgorden optreden i>j>k, j>k>i, k>i>j. Het aantal aspecten waarop i beter scoort dan j is groter dan het aantal aspecten waarop j beter scoort dan i, het aantal aspecten waarop j beter scoort dan k is groter dan het aantal aspecten waarop k beter scoort dan j, het aantal aspecten waarop k beter scoort dan i is groter dan het aantal aspecten waarop i beter scoort dan k....

Met het voorbeeld met zeven oplossingen stellen we nu een nieuwe tabel op. Aangezien we in deze methode oplossingen twee aan twee evalueren, vinden we de oplossingen zowel in de rijen als de kolommen terug, waarbij we in de cel aangeven voor hoeveel aspecten de oplossing in de rij beter scoort dan de oplossing in de kolom. Het zal hierbij opvallen dat we "klasse" als beter waarderen dan een "ordinair". Dat geeft natuurlijk aan waar de methode faalt aangezien er geen orde gedefinieerd kan zijn tussen twee nominale waarderingen.

Neem als voorbeeld van waardering de rij die oplossing 1 ten opzichte van de andere evalueert: 1 scoort beter dan 2 op één aspect: C; 1 scoort beter dan 3 op één aspect: B; 1 scoort beter dan 4 op twee aspecten: B en D; 1 scoort beter dan 5 op twee aspecten: B en C; 1 scoort beter dan 6 op één aspect: B; 1 scoort beter dan 7 op drie aspecten: B, C en D.

In de laatste kolom tellen we het aantal voorkeurstemmen bij elkaar.

Hieruit blijkt dat oplossing 1 met kop en schouder boven de andere uitsteekt en dat oplossing 7 duidelijk inferieur is. Maar kunnen we iets zinvol vertellen over de andere oplossingen? We kunnen natuurlijk wel het ander standpunt innemen en ons afvragen welke oplossing lager scoort en daar een som van nemen. Merk op dat zich hierbij enkel oplossing 7 afscheidt.

Hier speelt het aantal aspecten dus een grote rol. Dit geeft aan hoe belangrijk het is de globale aspecten die overblijven na al het ontwerpwerk goed te onderbouwen.

Rangorde som methode

Zolang we rangordes beschouwen kunnen we correct redeneren. Van zodra we echter, zoals in dit beslissingscriterium, rangordes gaan optellen dan veronderstellen we dat de eenheden in de verschillende criteria aan elkaar gelijk zouden zijn en sluipt er een intervalschaal binnen. We gaan er dus van uit dat alle criteria even belangrijk zijn.

Met het voorbeeld met zeven oplossingen stellen we nu terug een nieuwe tabel op. Aangezien we in deze methode oplossingen twee een twee evalueren kiezen we een referentiepunt (hier oplossing 7) en we stellen een oplossing die op een criterium beter scoort als + voor en een oplossing die minder scoort als -, een even goed score geven we aan als I (indifferent). In de onderste rijen is de som gegeven van +, - en I.

Op deze manier schijnen oplossing 1 en 3 sterker te zijn dan de referentie. We kunnen natuurlijk een andere referentie kiezen, nemen we bijvoorbeeld 3.

Hieruit kan besloten worden dat alle oplossingen, behalve 7, even sterk zijn als 3.

Gewogen beslissingen

In de volgende heuristieken gaan we een aspect bijvoegen bij de gemeten aspecten, namelijk een “belang”, waarvan we veronderstellen dat het nul kan zijn en maximaal kan zijn en waarvan het verschil tussen nul en maximaal de eenheid van belang numeriek weergeeft. We kunnen dat onderbouwen doordat we in de reeds besproken heuristieken moesten veronderstellen dat de criteria even waardevol waren om een som te kunnen verantwoorden die ons een beslissingscriterium op één as kon verschaffen. Voor elke stakeholder kan dat anders zijn en dus kunnen we ook beslissingsheuristieken maken die stakeholder afhankelijk zijn. Immers: veel stakeholders zijn in staat het belang van een aspect voor zichzelf in te schatten.

We vullen nu het fictief voorbeeld aan, waarbij de waarderingen van 7 oplossingen voor 4 aspecten gedocumenteerd worden, met een kolom die het belang numeriek kwantificeert en waarbij de som van de waarderingen van belang maximaal is (100%):

Lexicografisch criterium methode

In de tabel zijn de criteria naar belang geordend. In de lexicografische methode is dit zeer handig omdat we dan onmiddellijk zien dat er maar één oplossing is die het laagst (het hoogst) scoort op aspect A, en die wordt gekozen. Veronderstel nu dat de laagste score zou gekozen worden maar dat oplossing 7 niet zou gevonden zijn, dan zijn er drie (4, 5, 6) met laagste A, dus gaan we naar het volgende criterium waarbij 6 als oplossing verworpen wordt. Bij het evalueren van het volgende aspect is duidelijk dat 4 de beste oplossing is volgens de lexicografische methode ongeacht de waardering voor D die oplossing 5 zou hebben.

De lexicografische methode is zeer eenvoudig toepasbaar maar gaat er van uit dat er geen (eventueel complexe) samenstellingen van waarderingen te bedenken zijn die gezamenlijk waardevoller zijn dan een waardering op het belangrijkste aspect. Er is dus geen substitutie van aspecten mogelijk.

De concordantie index methode

Met behulp van de waarderingen van belang kunnen we nu een concordantie index opbouwen, een mate van overeenstemming met een op voorhand geponeerd belang. Aspecten worden hierbij niet meer als gelijkwaardig beschouwd, en het die eenheid van gelijkwaardigheid die we kunnen optellen. Men behandelt aspecten hier dus als stemmers voor i of j waarbij elke stem een ander gewicht heeft. Dat betekent dat de rangorde som methode bijvoorbeeld er van uit ging dat de vier aspecten even belangrijk waren en dus voor 25% in geheel belang meegeteld konden worden, nu echter veronderstellen we dat de verdeling van het belang niet meer gelijk is.

Voorbeeld van berekening: de voorkeursrelatie van 2 over 1 wordt berekend door 45 (A) + 25 (B) + 15 (D) = 85. De eenheid is natuurlijk 100(%). Merk op dat, bij gelijke waardering, het belang ook meegerekend wordt. Dit betekent dat deze methode ook rekening houdt met de waarnemingsresolutie van "gelijkheid" die dan voor beide voorkeursrelaties gewaardeerd wordt. De concordantie indexen worden in de volgende tabel gegeven.

Het hoogste getal in de tabel is 85. Dit betekent dat 85 maximaal rekening houdt met vergelijkbare waarderingen in de gekozen voorkeursrelatie. Enkel die waardering gebruiken we nu om de voorkeursrelatie als een pijl in het volgende diagram te representeren:

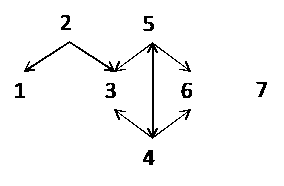
Omdat er een pijl is van 4 naar 5 en ook van 5 naar 4 is het duidelijk dat we oplossing 4 en 5 als gelijkwaardig zullen beschouwen, en we zien ook dat er twee kernen zijn waarmee we verder werken: {2,4,7} en {2,5,7}. Merk op dat 7 zich hier onderscheidt van de rest omdat de maximaal vergelijkbare waardering niet voorkomt bij 7. We interpreteren deze situatie dat 7 een onvergelijkbaar alternatief is en dus kunnen we het met deze methodiek niet als "beter of slechter" dan de andere uitsluiten. Maar als we nu kritisch genoeg zijn dan merken we ook dat het verschil tussen 4 en 5 eigenlijk mee gebaseerd is op aspect D en dit mocht eigenlijk niet ordinaal gewaardeerd worden aangezien het enkel een nominale meting was.