We merken nu op dat de projectoren in hun functie als basis nog op een andere manier met het matrix formalisme voor te stellen zijn. We kunnen immers een willekeurig punt h dat we voorstellen in het modulo3 signatuurbit formaat opsplitsen in twee soorten componenten: de componenten met signatuur +, en de componenten met signatuur -. Het gecollapste punt <>⊕<h>, dat in bitstring enkel componenten met plus-signatuur toont, geeft de oorspronkelijke componenten met plus-signatuur, het gecollapste punt <<>>⊕<h>, dat in bitstring enkel componenten met min-signatuur toont, geeft de oorspronkelijke componenten met min-signatuur. In beide gevallen zijn de componenten van deze gecollapste haakvectoren deze van het oorspronkelijk punt, de oorspronkelijke haakvector.
Elke welgevormde haakuitdrukking h is dus als een directe som van twee gecollapste haakvectoren uit te drukken die we als volgt kunnen noteren: h(<>⊕<h>) en h(<<>>⊕<h>). Dus h=h(<>⊕<h>)⊕h(<<>>⊕<h>)=(<>⊕<h>)⊕(<<>>⊕<h>)
h(<>⊕<h>) is uit te drukken als een som van gecollapste plus-signatuur atomen (OR-atomen).
h(<<>>⊕<h>) is uit te drukken als een som van gecollapste min-signatuur atomen (AND-atomen).
De ruimte van <>⊕<h> is orthogonaal met de ruimte van <<>>⊕<h>. Samen spannen ze een ruimte op die de directe som is van de beide ruimten. Conventioneel wordt een ruimte opgespannen door een basis. We kunnen deze gecollapste punten dus als orthogonale basisvectoren gebruiken die de ruimte {<>⊕<h>, <<>>⊕<h>} opspannen. Conventioneel wordt er met de positieve projectoren van de ruimte gewerkt en dat is in dit geval dus {<>⊕<h>, <>⊕h}. Dus in haakvector formaat kunnen we h in zijn eigen basis uitdrukken als h=<<>>•(<>⊕<h>)⊕<>•(<>⊕h). Inderdaad is dit gelijk aan <>⊕<h>⊕<<>>⊕<h>. We merken op dat de splitsing van de plus-bits en de min-bits door de coëfficiënt van de basisvectoren gecodeerd wordt, <<>> als de coëfficiënt van (<>⊕<h>), <> als de coëfficiënt van (<>⊕h).
h=<<>>•(<>⊕<h>)⊕<>•(<>⊕h) is nu op verschillende manieren te vertalen in matrixnotatie:
![]() en de basis is dus als kolommatrix te noteren als
en de basis is dus als kolommatrix te noteren als
![]() ,
inderdaad dit is een concrete invulling van de kolom matrix (x y)T.
,
inderdaad dit is een concrete invulling van de kolom matrix (x y)T.
Elke haakvector is dus als de component-gewijze vermenigvuldiging
(of dot product) te beschouwen van twee kolom matrices:
![]() en
en
![]() of
als conventionele matrix vermenigvuldiging als de vermenigvuldiging
van een rijmatrix en een kolommatrix
of
als conventionele matrix vermenigvuldiging als de vermenigvuldiging
van een rijmatrix en een kolommatrix
![]()
We kunnen h ook uitdrukken in een andere basis: h=h•(<>⊕<w>)⊕h•(<>⊕w) inderdaad is dit gelijk aan <h>⊕<h•w>⊕<h>⊕h•w. En dus kunnen we h ook uitdrukken in een nog andere basis: h=h•(<>⊕<v>)⊕h•(<>⊕v) inderdaad is dit gelijk aan <h>⊕<h•v>⊕<h>⊕h•v. Andere basissen worden bereikt door haakvector vermenigvuldiging.
w•h=w•(<>⊕<h>)⊕<w>•(<>⊕h)=h•(<>⊕<w>)⊕<h>•(<>⊕w)
Een niet-orthogonale basis is ook te construeren. We merken op dat
er geldt dat h=<h>•(<<>>)⊕<>•(h).
Dus elke haakvector is als de component-gewijze vermenigvuldiging
(dot product) te beschouwen van twee kolom matrices:
![]() en
en
![]() of
dus als matrixvermenigvuldiging van een rij- en een kolommatrix
of
dus als matrixvermenigvuldiging van een rij- en een kolommatrix
![]()
De basissen
![]() en
en
![]() zijn
in elkaar te transformeren met behulp van de H2 Hadamard
operator.
zijn
in elkaar te transformeren met behulp van de H2 Hadamard
operator.
Inderdaad
![]() en
en
![]()
Dit is uiteraard uit te breiden naar verschillende equivalente voorstellingen van haakvectoren als matrixvermenigvuldiging van basisvectoren, en verder ook als Hadamard operatoren.
Bijvoorbeeld voor het haakformalisme is er geen verschil tussen de volgende twee matrixvermenigvuldigingen van verschillende rijmatrices met dezelfde kolommatrix:
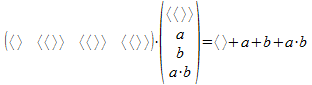 en
en
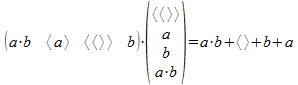
De rechterkant van het gelijkheidsteken is dank zij de commutativiteit van de som dezelfde haakvector.
Met deze vertaling van het haakformalisme naar matrixnotatie komt een belangrijk nieuw model te beschikking: elke haakvector is als de component-gewijze vermenigvuldiging te beschouwen van twee of meer kolommatrices. Inderdaad h(<>⊕<h>) is uit te drukken als een som van gecollapste plus-signatuur atomen en h(<<>>⊕<h>) is uit te drukken als een som van gecollapste min-signatuur atomen en elk van deze kan nu als kolommatrix uitgedrukt worden. Er zijn dus zoveel kolommen te gebruiken als het aantal atomen, dus voor een n-onderscheidingen universum kunnen we maximaal 2n kolommen inzetten, maar we hoeven dat niet te doen, trouwens sommige welgevormde haakvectoren zijn op een lager onderscheidingen universum af te beelden en meer dan de strikt noodzakelijke atomen inzetten maakt het inzicht enkel moeilijker!
Dat bepaalde structuren door sommige transformaties niet beïnvloed worden is een evidentie in het haakformalisme (een haakuitdrukking h hoeven we niet te expliciteren in zijn opbouwende onderscheidingen, elke bit kan een eigen structuur krijgen). Conventioneel wordt dat teruggevonden wanneer men spreekt van tensoren (structuren van getallen) die door bepaalde transformaties niet veranderen.