Werk-in-uitvoering, af te werken na “hier verder”.

Het creatief product is associatief indien als toegevoegde onderscheiding telkens dezelfde gebruikt wordt. Onder die voorwaarde (die enkel relevant is voor het combineren van creatieve producten met behulp van het creatief product zelf) zal er met conjunctie en disjunctie ook onderzocht worden welke structuur hier ontstaat.

We geven hiervan het voorbeeld van het creatief product en zijn niet commutatieve variant. We kunnen daar twee tralies van onderscheiden:

• de tralie met (x⊗y)_z en (y⊗x)_z als opspannende welgevormde haakuitdrukkingen.

• de tralie met(x⊗<y>)_z en (<y>⊗x)_z als opspannende welgevormde haakuitdrukkingen.

(x⊗y)_z en (y⊗x)_z

We onderzoeken eerst de structuur die opgespannen wordt door het creatief product (x⊗y)_z ∼ <z<x>><<z><y>> en zijn niet commutatieve variant (y⊗x)_z ∼ <z<y>><<z><x>>. Beide hebben ze natuurlijk ook hun inbedding die deel zal uitmaken van dezelfde structuur. Hiertoe is het nodig en voldoende om de mogelijke conjuncties en disjuncties van de vier betrokken welgevormde haakuitdrukkingen te bepalen, maar ook is het nuttig de exclusieve disjunctie te berekenen. We geven hieronder een paar voorbeelden van de berekening.

Disjunctie

<z<x>><<z><y>>OR<z<y>><<z><x>> is in welgevormde haakuitdrukking <z<x>><<z><y>><z<y>><<z><x>> die we dan reduceren als volgt:

<z<x>><<z><y>><z<y>><<z><x>>

<<<z>><x>><<z><y>><z<y>><<z><x>>

<<<z><<z><x>>><x<<z><x>>>><<z<z<y>>><y<z<y>>>>

<<<z><<x>>><x<<z><>>>><<z<<y>>><y<z<>>>>

<<<z>x><x>><<zy><y>>

<<x>><<y>>

xy

<z<x>><<z><y>>OR<zy><<z>x> is in welgevormde haakuitdrukking <z<x>><<z><y>><zy><<z>x> die we dan reduceren als volgt:

<z<x>><<z><y>><zy><<z>x>

<z<x>><zy><<z>x><<z><y>>

<<<z<x>><zy>>><<<<z>x><<z><y>>>>

<<<<x>><y>>z><<<x><<y>>><z>>

<<x<y>>z><<<x>y><z>>

Exclusieve disjunctie

Het is interessant om <z<x>><<z><y>>XOR<z<y>><<z><x>> te berekenen. Dit is de welgevormde haakuitdrukking:

<<z<x>><<z><y>><<z<y>><<z><x>>>><<<z<x>><<z><y>>><z<y>><<z><x>>>

<<<z<y><<z><y>>><<z><x><z<x>>>>><<<z<x><<z><x>>><<z><y><z<y>>>>>

<z<y>><<z><x>><z<x>><<z><y>>

<<z<z<x>>><x<z<x>>>><<z<z<y>>><y<z<y>>>>

<<x>><<y>>

xy

We merken dus dat OR en XOR niet onderscheiden zijn. Hieruit kunnen we onmiddellijk afleiden dat AND en XNOR evenmin zullen onderscheiden zijn.

In overzicht:

We berekenen hiermee het volgende niveau dat met de disjunctie kan bereikt worden.

OR van de eerste rij

xy<<x<y>>z><<<x>y><z>>

xy<<<>>z><<<>><z>>

xy<z>z

<>

OR van de diagonaal met de creatieve producten

<<<x>y>z><<x<y>><z>><<x<y>>z><<<x>y><z>>

<<<x>y>z><<x<y>>z><<<x>y><z>><<x<y>><z>>

<<<<<x>y>z><<x<y>>z>>><<<<<x>y><z>><<x<y>><z>>>>

<<<<<x>y>><<x<y>>>>z><<<<<x>y>><<x<y>>>><z>>

<<<x>yx<y>>z><<<x>yx<y>><z>>

<<<>>z><<<>><z>>

<z><<z>>

<>

AND van de diagonaal met de creatieve producten

<<<<<x>y>z><<x<y>><z>>><<<x<y>>z><<<x>y><z>>>>

<<<<<x>y>z<<<x<y>>z><<<x>y><z>>>><<x<y>><z><<<x<y>>z><<<x>y><z>>>>>>

<<<<<x>y>z<<<x<y>>><<<x>y><>>>><<x<y>><z><<<x<y>><>><<<x>y>>>>>>

<<<<<x>y>z<<<x<y>>>>><<x<y>><z><<<<x>y>>>>>>

<<<z><<z>>><x<y>><<x>y>>

<<x<y>><<x>y>>

Conjunctie

<z<x>><<z><y>>AND<z<y>><<z><x>> is in welgevormde haakuitdrukking <<<z<x>><<z><y>>><<z<y>><<z><x>>>> en dit reduceren we:

<<<z<x>><<z><y>>><<z<y>><<z><x>>>>

<<<z<x><<z<y>><<z><x>>>><<z><y><<z<y>><<z><x>>>>>>

<<<z<x><y>><<z><y><x>>>>

<<x><y><<z><<z>>>>

<<x><y>>

<z<x>><<z><y>>AND<zy><<z>x> is in welgevormde haakuitdrukking <<<z<x>><<z><y>>><<zy><<z>x>>> en dit reduceren we:

<<<z<x>><<z><y>>><<zy><<z>x>>>

<<<z<x><<zy><<z>x>>><<z><y><<zy><<z>x>>>>>

<<<z<x><<y><<>x>>><<z><y><<<>y><x>>>>>

<z<x>y><<z><y>x>

<<x>yz><x<y><z>>

In overzicht:

We berekenen hiermee het volgende niveau dat met de conjunctie kan bereikt worden.

AND van de eerste rij

<<x><y><<<x>yz><x<y><z>>>>

<<x><y><<<>z><<><z>>>>

<<>>

AND van de diagonaal met creatieve producten

<<<x<y>z><<x>y<z>>><<<x>yz><x<y><z>>>>

<<<x<y>z<<<x>yz><x<y><z>>>><<x>y<z><<<x>yz><x<y><z>>>>>>

<<<x<y>z<<<><>><<>>>><<x>y<z><<<>><<><>>>>>>

<<<x<y>z<>><<x>y<z><>>>>

<<<<>><<>>>>

<<>>

Merk op dat de creatieve producten uit de tabel geen AND atomen zijn, ze kunnen immers zowel als AND en als OR geschreven worden, en toch sluiten ze elkaar uit. Bijvoorbeeld: <x<y>z><<x>y<z>> is als disjunctie geschreven en dezelfde welgevormde haakuitdrukking kan ook als conjunctie geschreven worden als volgt: <<<x>yz><x<y><z>>>.

Een analoge redenering gaat natuurlijk ook op voor de inbeddingen van de vier punten uit de AND tabel.

We kunnen ook de disjunctie berekenen van de vier punten uit de tabel, bijvoorbeeld de OR van de diagonaal met creatieve producten:

<x<y>z><<x>y<z>><<x>yz><x<y><z>>

<x<y>z><<x>yz><<x>y<z>><x<y><z>>

<<<x<y>z><<x>yz>>><<<<x>y<z>><x<y><z>>>>

<<<x<y>><<x>y>>z><<<<x>y><x<y>>><z>>

<<<<<x<y>><<x>y>>z><<<<x>y><x<y>>><z>>>>

<<<x<y>><<x>y>><<z><<z>>>>

<<<x<y>><<x>y>><<>>>

<x<y>><<x>y>

Tralie

We kunnen nu de totale structuur in een tralie voorstellen:

Dit is een volwaardige tralie want elk koppel punten heeft een infimum en een supremum, maar terwijl er voor de tralie van twee onderscheidingen alleen op het centraal niveau punten te vinden zijn die niet alle onderscheidingen nodig hebben, vinden we hier op de drie niveaus van de tralie punten die de toegevoegde onderscheiding z niet nodig hebben.

Het speciale van deze ordening komt tot uiting wanneer we enkel nog de creatieve producten met z weergeven, die geen totale tralie meer maken.

(x⊗<y>)_z en (<y>⊗x)_z

Het is nu eenvoudig om ook de structuur voor te stellen in tralie vorm die opgespannen wordt door het creatief product (x⊗<y>)_z ∼ <z<x>><<z>y> en zijn niet commutatieve variant (<y>⊗x)_z ∼ <zy><<z><x>>.

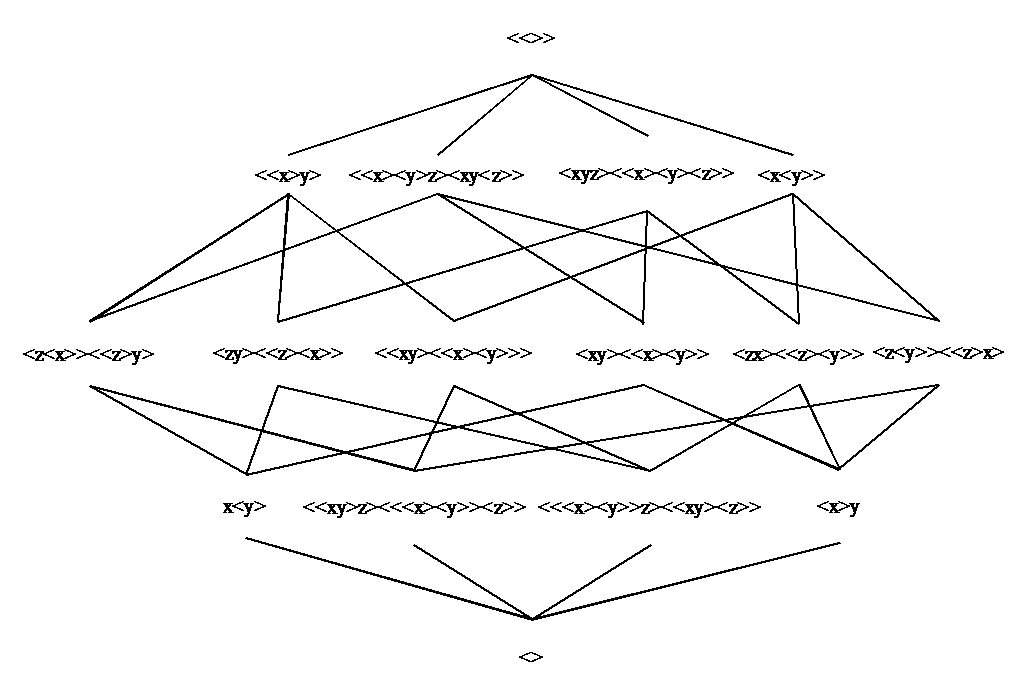
Uiteraard kunnen we ook de structuur voorstellen met enkel de welgevormde haakuitdrukkingen met de toegevoegde onderscheiding z.

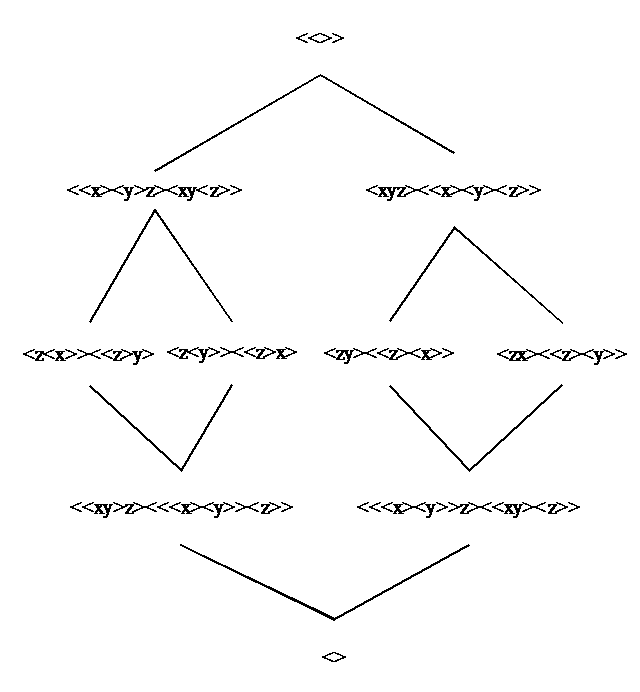
Noteer

De tralie opgespannen door (x⊗y)_z en (y⊗x)_z en de tralie opgespannen door (x⊗<y>)_z en (<y>⊗x)_z zijn met elkaar verbonden langs de twee welgevormde haakuitdrukkingen op centraal niveau zonder de toegevoegde onderscheiding z. Inderdaad <<xy><<x><y>> is niet verschillend van <x<y>><<x>y> en <xy><<x><y> is niet verschillend van <<x<y>><<x>y>>. Dit geeft al de indicatie dat we nu een nieuwe tralie kunnen onderzoeken die door beide tralies gegenereerd zal worden. Inderdaad zullen conjunctie en disjunctie van punten uit beide tralies nieuwe welgevormde haakuitdrukkingen genereren. Bijvoorbeeld voor disjunctie van twee termen op niveau 3:

<<x>yz><x<y><z>><<x><y>z><xy<z>>

<<<<x>yz><<x><y>z>>><<<x<y><z>><xy<z>>>>

<<<y><<y>>><x>z><<<<y>><y>>x<z>>

<<x>z><x<z>>

Door de constructie is duidelijk dat de conjunctie van dezelfde termen hiervan de inbedding zal geven. Beide zijn punten die niet in de oorspronkelijke tralies voorkomen.

Bijvoorbeeld voor disjunctie van een term op niveau 3 en een term op niveau 1:

<<x>yz><x<y><z>><<xy>z><<<x><y>><z>>

<<<<x>yz><<xy>z>>><<<x<y><z>><<<x><y>><z>>>>

<<<<x>y><<xy>>>z><<<x<y>><<<x><y>>>><z>>

<<xy>z><<<x><y>><z>>

Door de constructie is duidelijk dat de conjunctie van dezelfde termen hiervan de inbedding zal geven, die we in dit geval ook kunnen voorstellen als de disjunctie <xyz><<x><y><z>>. Beide zijn punten die wel in de oorspronkelijke tralies voorkomen.

Bijvoorbeeld voor de disjunctie van een term op niveau 3 en een op centraal niveau

<<x>yz><x<y><z>><z<x>><<z>y> Hier verder

De tralie structuren ontstaan met de operaties die simultaneïteit kunnen uitdrukken: conjunctie en disjunctie. We kunnen ook onderzoeken welke welgevormde haakuitdrukkingen ontstaan met een associatief creatief product als operatie.

<zx><<z>y> creatief vermenigvuldigen met <z<y>><<z><x>> is dus de welgevormde haakuitdrukking <z<<zx><<z>y>>><<z><<z<y>><<z><x>>>>. We reduceren deze:

<z<<zx><<z>y>>><<z><<z<y>><<z><x>>>>

<z<<x><<>y>>><<z><<<><y>><<x>>>>

<z<<x>>><<z><<<x>>>>

<zx><<z><x>>

<x•z>

In overzicht:

Door niet commutativiteit geldt dan:

Terwijl x en y zich onvermijdelijk op centraal niveau bevinden in de tralie opgespannen door x, y en z zullen x•z en y•z zich op tussen niveaus bevinden.